The Oil and Vinegar Signature Scheme - We are not making food

Introduction

Let's ensure we understand the foundational concepts before delving further into the subjects. Here is a brief introduction if you are unfamiliar with the Signature Schemes.

A signature scheme is a mathematical scheme for verifying the authenticity of digital messages or documents.

✔️ Key generation: private key, public key.

✔️ Signing: given a message and a private key, produce a signature.

✔️ Verifying: given the message, public key, and signature, either accepts or rejects   the message’s claim to authenticity.
 

This article explains the details of The Oil and Vinegar Signature Scheme, in which we will talk about Signing and verification keys, Signature creation, Signature validation, and Problems and advantages.

Without further ado, let's get started.

Unbalanced oil and vinegar scheme

🎯 The oil and vinegar scheme created by J. Patarin has been updated and is known as the unbalanced oil and vinegar (UOV) scheme in the field of cryptography. 

🎯 Each protocol uses a digital signature. They are forms of multivariate cryptography.

🎯 Based on an NP-hard mathematical problem, this signature scheme's security is ensured. 

A minimal quadratic equation system must be resolved to generate and verify signatures. NP-hardness exists for m equations with n variables. For cryptographic purposes, it is crucial to note that the problem is challenging in the typical scenario where m and n are close to being equal, even when utilising a quantum computer. The problem is straightforward if m is significantly greater or lower than n. Various signature schemes have been developed based on multivariate equations to establish quantum resistance.

The key size of UOV might be huge, which is a big disadvantage. The number of equations, m, is typically selected to be double the number of variables, n. For a system that would provide security comparable to the Digital Signature Algorithm or Elliptic Curve Digital Signature Algorithm, it would need a lot of space to encode the coefficients of all these equations in the key—at least 200 kilobytes.

Signing and verification key

A signature scheme consists of a signing key that is kept secret and a verification key made available to the public. For instance, the keys are both exponents in RSA-based signature methods. The keys are more complicated in the UOV scheme than in any other multivariate signature system.

Solving m equations with n variables is the subject of the mathematical problem. The public key is the entire set of equations.

A mathematical issue must be changed before it can be used for cryptography. It would take a lot of resources to compute the n variables. A typical computer in a reasonable amount of time cannot compute this. As a result, a unique Trapdoor is added to the system of equations. The key to the trapdoor is the signing. A polynomial vector P' and two affine transformations, T and S, make up its three components. Both transformations are applied to particular groupings of items. T converts y into y₁, y₂, y₃,...... y_n. The valid signature is produced by the second transformation, S, which transforms the variable vector
 

Tools for creating the equations are provided by the third hidden element P'. Only the owner of the signature key is aware of the rules used to construct the equations.

Signature creation

💁 The following equation system needs to be solved in order to produce a valid signature.

y₁ = f₁*(x₁,x₂,x₃…..,x_n)

y₂ = f₂*(x₁,x₂,x₃…..,x_n)

    :

    :

y_m = f_m*(x₁,x₂,x₃…..,x_n)

Here, the message to be signed is supplied by the notation y = (y₁, y₂, y₃,..., y_m). The valid signature is x = (x₁,x₂,x₃…..,x_n).

The message must be altered in order to meet the equations system before signing a specific y. T is used to "divide" the message into manageable bits, as seen by the expression y = (y₁, y₂, y₃,..., y_m). The equations must then be constructed. The form of each equation is the same:

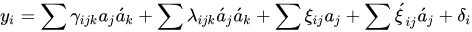
💁 A valid signature x is produced after the following steps, which sign the given message y.

☑️ It is necessary to select the coefficients,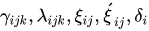 discreetly.

☑️ The variables for vinegar (a_j') are selected at random.

☑️ Solving the ensuing system of linear equations for the oil variables a'_i.

The pre-signature A = (a₁,...,a_n,a₁',...,a_v') is constructed from the vinegar and oil variables. In order to get the legal signature 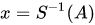, A is finally changed by the private transformation S.

If the vinegar variables are constant and the oil variables are not multiplied by one another in the equation, the equation system becomes linear. As a result, it is simple to compute the oil variables using, for instance, a Gaussian reduction approach. The process of creating a signature is quick and simple computationally.

Signature validation

💁 The communication partner receives the signature. With the aid of the public key, which is a system of equations, the signature is verified.

y₁ = f₁*(x₁,x₂,x₃…..,x_n)

y₂ = f₂*(x₁,x₂,x₃…..,x_n)

    :

    :

y_m = f_m*(x₁,x₂,x₃…..,x_n)

The equations required to create a signature are slightly different from the mathematics used in this system. It has been altered to prevent attackers from learning the confidential coefficients and unique formatting of the oil and vinegar variables. To verify the signature, each public key equation must be solved. The signature itself serves as the input. The verification was successful if each result y_i matched its corresponding portion of the original message.

Problems and advantages

The algorithm's key benefit is that the mathematical problem it must answer is resistant to quantum effects. Commercial signature methods like RSA or ElGamal rely on the discrete logarithm issue being intractable and broken if a quantum computer can factor big composite numbers using Shor's Algorithm. Since no algorithm gives a quantum computer a significant edge in solving multivariate systems of equations, UOV may continue to be secure.

The second benefit is that the equations' operations are rather straightforward. This signature can be used with low-resource hardware, such as that present in smart cards because signatures can only be formed and validated by adding and multiplying "little" values.

The public key for UOV involves the full system of m equations, which can take up several hundred kilobytes, which is a drawback. UOV hasn't been applied frequently. Even though there are now a few known attack strategies, if UOV gains popularity, others could emerge. Because more research needs to be done on UOV's security, it is not yet ready for commercial use.