The post correspondence problem is an undecidable decision problem introduced by Emil post in 1946. The post correspondence problem consists of two strings, A and B, of equal input. The two lists of strings are A =y1,y2,y3…,yn , B= x1,x2,x3….xn, then there exists a non-empty list of integers i1,i2,i3…. Such that, x1,x2,x3…xn = y1,y2,y3…..yn.
There is N number of dominos in this problem, also known as tiles. The task is to arrange dominos so that strings made by the numerator and strings produced by the denominator are equal.
Post correspondence problem is an undecidable problem. It was introduced by Emil Post in 1946. Here in this problem, there is N number of dominos, i.e., tiles. And we have to arrange the dominos in such a way that the string produced by the denominators and the numerators is same.
Post Correspondence problem can be represented in two ways:
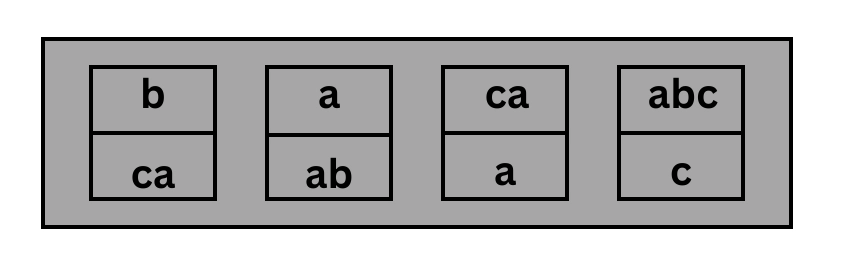
1. Domino’s Form
2. Table form
Example of Post Correspondence Problem
Example 1:
A
B
1.
1
111
2.
10111
10
3.
10
0
Explanation:
Step-1: First, we will start with a domino in which the first symbol at the top and the first symbol at the bottom is the same. In this example, we will go with the second domino.
The string at the top is 10111, and the string at the bottom is 10.
A: 1 0 1 1 1
B: 1 0
Step-2: Now, we need 1’s in the denominator to match the 1’s in the numerator; we will go with the first domino. The string at the top is 10111 1, and the string at the bottom is 10111.
A: 1 0 1 1 1 1
B: 1 0 1 1 1
Step-3: Now, there is an extra 1 in the numerator, and to match this 1, we will add the first domino again in sequence. The string at the top is 1011111, and the bottom is 10111111.
A: 1 0 1 1 1 1 1
B: 1 0 1 1 1 1 1 1
Step-4: Now there is an extra 1 in the denominator, and to match it, we will add the third domino; the string at the top is 101111110, and the string at the bottom is 101111110.
A: 1 0 1 1 1 1 1 1 0
B: 1 0 1 1 1 1 1 1 0
Sequence for this solution is: 2 1 1 3
Example 2:
Numerator
Denominator
1
B
CA
2
A
AB
2
CA
A
4
ABC
C
Explanation:
Step-1: We will start with a domino in which 1st symbol at the numerator and the first symbol at the denominator are the same. So we will choose domino 2.
A: A
B: A B
Step-2: Now, we need B in the numerator and denominator to match the numerator; we will go with domino 1.
A: A B
B: A B C A
Step-3: Now, for matching the denominator, we will add domino 3 for matching the numerator.
A: A B C A
B: A B C A A
Step-4: There is an extra A in the denominator, so to match the string, we will add domino 2. A: A B C A A B: A B C A A A B
Step-5: There is an extra AB in the denominator; to match it, we will add domino 4. The string in the denominator and numerator is ABCAAABC and ABCAAABC, respectively.
A: A B C A A A B C
B: A B C A A A B C
Sequence: 21324
Proof of undecidability
Undecidability of a problem means that there is no particular algorithm that can determine whether a given problem has a solution or not. A common undecidable problem is a Turing problem, so its undecidability is also proved if we can reduce the Turing problem into post Correspondence problem.
Consider an instance of a post correspondence problem that can simulate the computation of an arbitrary Turing Machine on random input. A match will occur if the Turing machine accepts the input. The problem of deciding whether a Turing machine will accept the given information or not is a well-known problem. As the post Correspondence problem reduces to this particular problem, we can say the post correspondence problem is undecidable, which completes our proof.
Post correspondence problem is an undecidable problem in automata. Here in this problem, there is N number of dominos, i.e., tiles. And we have to arrange the dominos in such a way that the string produced by the denominators and the numerators is same.
Why is post correspondence problem undecidable?
Because no specific method can tell whether a post correspondence problem has a solution or not, the postman correspondence problem is intractable. The technique for proving the theorem can be done in a number of ways, but they are all essentially the same.
What is the difference between post correspondence problem and modified post correspondence problem?
Identifying whether a set of dominoes has a match or not is the Post's Correspondence Problem (PCP). Similar to PCP, the modified Post's Correspondence Problem (MPCP) just requires that we specify the set of tiles as well as a particular tile.
What is silly post correspondence problem?
A set of dominoes S is in the silly Post Correspondence Problem (SPCP) if and only if S contains a piece whose top string perfectly matches the bottom string. As a result, SPCP is decidable in nature.
Conclusion
In this article, we have extensively discussed the postman correspondence problem. We started with what domino or tile is, then we saw some examples of how to solve PCP, and then the proof of undecidability.
After reading about the target machines, are you not feeling excited to read/explore more articles on the topic of compiler design? Don’t worry, Coding Ninjas has you covered. To learn, see the compiler design course, and you can visit our website coding ninjas!
46+ registered 