What sorting algorithm does sort function in C++ use? Also, what is its time complexity?

Inbuilt C++ sorting uses a mergesort algorithm and runs in O(NlogN) time where N is the number of elements in the array that need to be sorted.

Other than the sorting algorithm, which other approach can you use to solve the problem?

We can use the divide and conquer algorithm since mergesort is itself based on the divide and conquer algorithm leading to the O(NlogN) improved time complexity.

What is the time complexity of insertion and deletion from a min-heap or max-heap?

Both insertion and deletion in max/min-heap costs O(NlogN).

Table of contents

Introduction

Problem Statement

Approach 1: Brute Force

3.1.

Code

3.2.

Complexity Analysis

3.2.1.

Time Complexity: O(N2)

3.2.2.

Space Complexity: O(N)

Approach 2: Sorting

4.1.

Code

4.2.

Complexity Analysis

Frequently Asked Questions

Key Takeaways

Last Updated: Mar 27, 2024

The Skyline Problem

Author Rhythm Jain

Introduction

Most people find The Skyline Problem a very complicated and hard problem to solve, although it is not so complicated. In this article, let me make this problem simple for you.

Before we start, if you don’t know about the Skyline Problem or if you want to give it a try yourself first, you can access the problem on Coding Ninjas Studio.

Recommended: Please try it on “Coding Ninjas Studio” before moving on to the solution approach.

So, let’s dive right into the actual problem statement.

Problem Statement

In a two-dimensional city, you are given 'N' rectangle buildings. Your job is to compute the skyline of these buildings, remove hidden lines, and return the skyline generated by all of them. When viewed from a distance, a city's skyline is the outside contour of the silhouette made by all of the buildings in that city. BUILDINGS[i] = [LEFT i, RIGHT i, HEIGHT i]: The geometric information of each building is given in the array of buildings:

-> LEFT_i is the x coordinate of the left edge of the ith building.

-> RIGHT_i is the x coordinate of the right edge of the ith building.

-> HEIGHT_i is the height of the ith building.

You may assume that all structures are perfect rectangles resting on a perfectly flat surface at a height of zero.

The skyline should be represented as a list of "key points" arranged by x-coordinate [[x1, y1], [x2, y2],...]. Except for the last point in the list, which always has a y-coordinate of 0 and is used to denote the skyline's conclusion where the rightmost building finishes, each key point is the left endpoint of some horizontal segment of the skyline. Any land between the leftmost and rightmost buildings should be included in the contour of the skyline.

NOTE:

In the output skyline, there must be no consecutive horizontal lines of similar height. For example, [...,[2 3], [4 5], [7 5], [11 5], [12 7],...] is not acceptable; in the final output, the three lines of height 5 should be merged into one.

For Example [..., [2 3], [4 5], [12 7],...]

In addition, the structures are arranged in a non-descending order.

Input Format

The first input line contains a single integer 'N,’ which represents the number of buildings to be provided.

The remaining 'N' lines include three space-separated integers: the left and right indices of the building's vertical edges, and the last integer specifies the building's height 'H.’

Output Format

Return a list of all the skylines that these buildings have created.

[[x1, y1], [x2, y2],...] should be used to represent the skyline as a list of "key points" arranged by their x-coordinate. Each key point is located on the left side of the page.

Except for the last point in the list, which always has a y-coordinate of 0 and is used to mark the termination of some horizontal segment in the skyline.

The rightmost building is when the skyline comes to an end. Any land between the leftmost and rightmost buildings should be included in the contour of the skyline.

For more clarification, see the below example.

Example

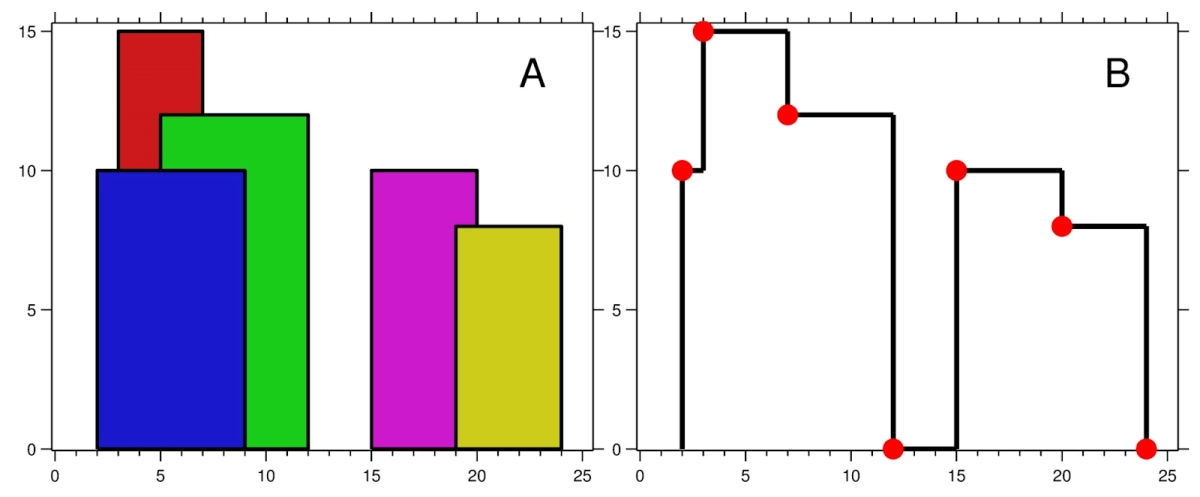
Assume we have the following input:

INPUT:

2 9 10

3 7 15

5 12 12

12 20 10

19 24 8

OUTPUT:

2 10

3 15

7 12

12 0

15 10

20 8

24 0

Explanation:

The below figure shows the buildings of the input. The adjacent figure shows the skyline formed by those buildings.

The red points in the adjacent figure represent the height of points in the output list.

SOURCE

Approach 1: Brute Force

The first answer is to get the height of each point on the line and then add the spot where the height changes. However, this would result in an excessive number of points.

An improvement is that the height adjustment can only occur at the building's left or right perimeter. Then we may combine the left and right boundaries to remove duplicates.

We determine the maximum height by traversing or structures for each left or right border. If pos>=building[0] && pos>=building[1], update the height. It should be noted that the right border does not count. Then all we have to do is add the pos whose height differs from the previous one.

Code

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> getSkyline(vector<vector<int>>& buildings) {
  int n=buildings.size();
  vector<int> keys;
  for(vector<int> building : buildings){
keys.push_back(building[0]);
keys.push_back(building[1]);
}
sort(keys.begin(),keys.end());
  int last=0;
  int lastKey=-1;
  vector<int> temp;
  vector<vector<int>> result;
  for(int left: keys){
  if(left==lastKey)
  continue;
lastKey=left;
  int height=0;
  for(vector<int> building : buildings){
  if(left>=building[0]&&left<building[1])
height=max(height,building[2]);
  else if(building[0]>left)
  break;
}
  if(height!=last){
temp.push_back(left);
temp.push_back(height);
result.push_back(temp);
temp.clear();
}
last=height;
}
  return result;
}

int main()
{
  vector<vector<int>> buildings={{2,9,10},{3,7,15},{5,12,12},{15,20,10},{19,24,8}};
  vector<vector<int>> ans=getSkyline(buildings);
  for(int i=0;i<ans.size();i++){
  cout<<ans[i][0]<<" "<<ans[i][1]<<endl;
}
  return 0;
}

Output:

2 10
3 15
7 12
12 0
15 10
20 8
24 0

Complexity Analysis

Time Complexity: O(N²)

Space Complexity: O(N)

Approach 2: Sorting

We first sort the critical points. Then, from left to right, scan through the critical points. When we come across the left border of a rectangle, we add it to the heap, using its height as the key. When we come across the right edge of a rectangle, we remove it from the heap.

When we hit the left edge of a building, we add it to the heap, and when we touch the right edge of a building, we continuously pop nodes off the top of the heap until the top node is a building whose right edge is still ahead.

The heap may contain buildings that have already been scanned, but that is irrelevant since we will discard them as soon as they reach the top of the heap. Finally, if we come across a critical point, we update the heap and set the height of that critical point to the value peeked from the heap's top.

Code

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
/*
Time Complexity: O(N * log(N))
Space Complexity: O(N)

where 'N' denotes the number of buildings present in the given problem.
*/
vector<vector<int>> getSkyline(vector<vector<int>>& buildings){

  /*
[start, -height, validUntil]
height > 0: start edge
height == 0: end edge
*/

  vector<vector<int>> edges;
  for(int i = 0; i < buildings.size(); i++){
  int x = edges.size();
edges.push_back(vector<int>());
edges[x].push_back(buildings[i][0]);
edges[x].push_back(-buildings[i][2]);
edges[x].push_back(buildings[i][1]);
}

  for(int i = 0; i < buildings.size(); i++){
  int x = edges.size();
edges.push_back(vector<int>());
edges[x].push_back(buildings[i][1]);
edges[x].push_back(0);
edges[x].push_back(1e9);
}

sort(edges.begin(), edges.end());

priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> prevHighest;

prevHighest.push({0, 1e9});

  vector<vector<int>> skyline;

  for(int i = 0; i < edges.size(); i++){

  int position = edges[i][0];
  int curHeight = -1*edges[i][1];
  int validUntil = edges[i][2];

  while(prevHighest.top().second <= position){
  /*
The equal term guarantees that, for end edges, popping
from height to low still works.
*/
prevHighest.pop();
}

  if(curHeight > 0){
  // Start edge.
prevHighest.push({-curHeight, validUntil});
}

  // prevHighest is now the current highest.

  if(skyline.size() == 0){
skyline.push_back(vector<int>());
skyline[0].push_back(position);
skyline[0].push_back(-prevHighest.top().first);
}
  else if(skyline.back()[1] != -prevHighest.top().first){
  int x = skyline.size();
skyline.push_back(vector<int>());
skyline[x].push_back(position);
skyline[x].push_back(-prevHighest.top().first);
}
}

  return skyline;
}


int main()
{
  vector<vector<int>> buildings={{2,9,10},{3,7,15},{5,12,12},{15,20,10},{19,24,8}};
  vector<vector<int>> ans=getSkyline(buildings);
  for(int i=0;i<ans.size();i++){
  cout<<ans[i][0]<<" "<<ans[i][1]<<endl;
}
  cout<<"Hello World";

  return 0;
}

Output:

2 10
3 15
7 12
12 0
15 10
20 8
24 0

Complexity Analysis

Time Complexity: O(NlogN), as it uses a mergesort algorithm

Space Complexity: O(N), sorting takes O(N) space in the worst case.

Frequently Asked Questions

What sorting algorithm does sort function in C++ use? Also, what is its time complexity?
Inbuilt C++ sorting uses a mergesort algorithm and runs in O(NlogN) time where N is the number of elements in the array that need to be sorted.
Other than the sorting algorithm, which other approach can you use to solve the problem?
We can use the divide and conquer algorithm since mergesort is itself based on the divide and conquer algorithm leading to the O(NlogN) improved time complexity.
What is the time complexity of insertion and deletion from a min-heap or max-heap?
Both insertion and deletion in max/min-heap costs O(NlogN).

Key Takeaways

Many complicated problems can be resolved through sorting techniques alone.

Performing Sorting also gives no. of algorithmic solutions that contain many other ideas such as:

Iterative
Divide-and-conquer
Comparison vs non-comparison based
Recursive

The key advantage of sorting is time complexity, which is crucial when solving a problem since it is not enough to be able to solve a problem; you must also be able to do it in the shortest amount of time feasible.

To learn more about sorting algorithms and different types of sorting algorithms, you can have a look at Sorting in Data Structures.

That's all for Today Coders!

Happy Coding

Live masterclass

Land an SDE Role at Google: Master DSA the smart way

by Saurav Prateek, SDE2@Google

19 Sep, 2024

01:30 PM

39+ registered

Become a Data Analyst at MAANG: Learn PowerBI for Data visualization

by Megna Roy, Senior Data Analyst @Amazon

17 Sep, 2024

01:30 PM

281+ registered

Learn Advanced Excel: Ace Data Analytics Interview

by Megna Roy, Data Analyst @ Amazon

15 Sep, 2024

06:30 AM

3871+ registered

Land an SDE Role at Google: Master DSA the smart way

by Saurav Prateek, SDE2@Google

19 Sep, 2024

01:30 PM

39+ registered

Become a Data Analyst at MAANG: Learn PowerBI for Data visualization

by Megna Roy, Senior Data Analyst @Amazon

17 Sep, 2024

01:30 PM

281+ registered

View more events