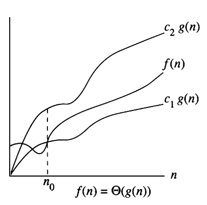
Theta-Notation(Θ) - Average case
This notation bounds a function within a constant factor.
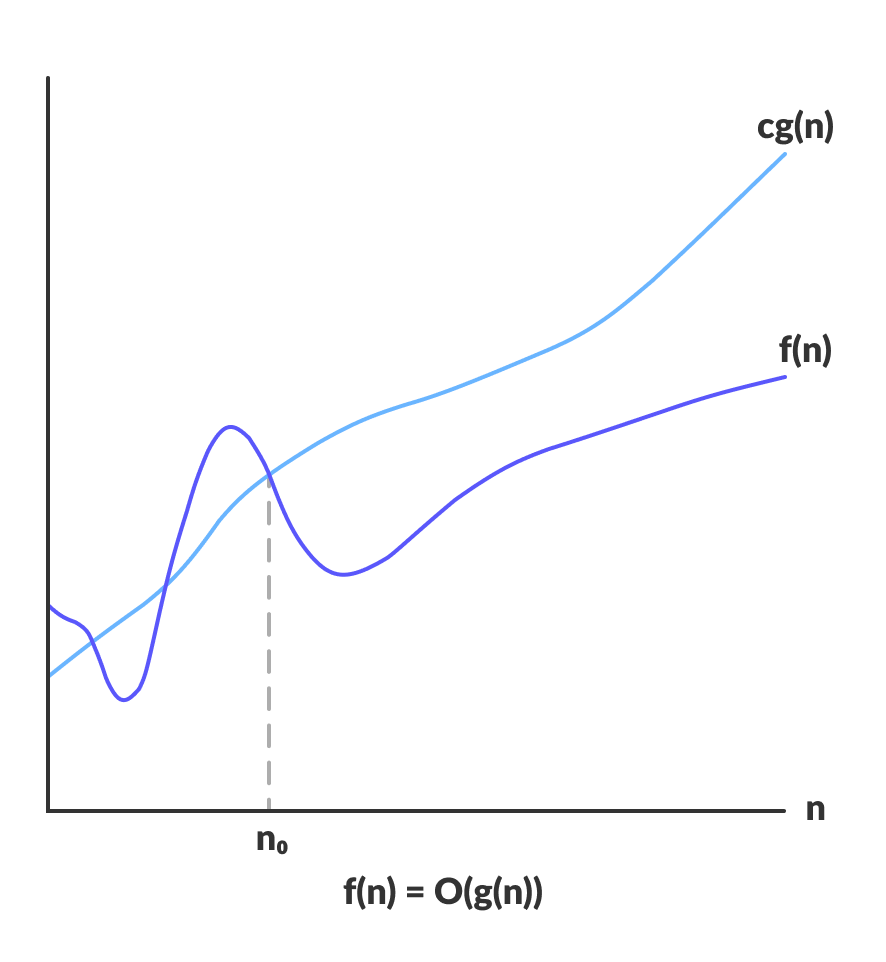
We say f(n) = g(n) if there exist positive constants n0, c1, and c2 in such a way that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0.
Pic from cs.fsu.edu.
Big Omega (Ω) - Best case
This notation gives a lower bound or the best case for a function within a constant factor.
We will write f(n) = g(n))when there are positive constants n0 and c such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0.
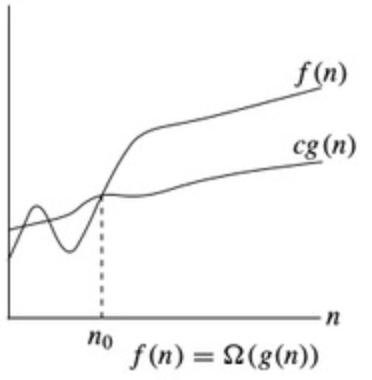
Pic from the medium.com
It will be more transparent when we see various examples of different time complexities.
Also see, kth largest element in an array
Must Read Lower Bound in C++
Example 1
public static void main(String[] args) {
System.out.println("Coding Ninjas");
}

You can also try this code with Online Java Compiler
Output
Coding Ninjas
As you can see, the above example is not based on the input size n, which is why the time complexity taken by this code will be O(1).
O(1) means a constant amount of time is required to execute the code.
Example 2
public static void main(String[] args) {
int n=3;
for(int i=0;i<n;i++)
System.out.println("Coding Ninjas");
}

You can also try this code with Online Java Compiler
Output
Coding Ninjas
Coding Ninjas
Coding Ninjas
In the above example, we have taken input n=3, applying the loop till input size n. ‘Coding Ninjas’ will be printed according to the input size given.
Therefore, this has a time complexity of O(n).
Example 3
public static void main(String[] args) {
int n=3;
for(int i=0; i < n; i++) {
for(int j=0; j < n;j++) {
System.out.println("Coding Ninjas");
}
}
}

You can also try this code with Online Java Compiler
Output
Coding Ninjas
Coding Ninjas
Coding Ninjas
Coding Ninjas
Coding Ninjas
Coding Ninjas
Coding Ninjas
Coding Ninjas
Coding Ninjas
In the above example, we have taken input n=3, applying the nested loops to input size n. ‘Coding Ninjas’ will be printed n*n times.
Therefore, this has a time complexity of O(n^2).
Example 4
public class BinarySearchJavaIterative {
// Returns index of x if it is present in arr[],
// else return -1
static int binarySearch(int arr[], int target) {
int left = 0, right = arr.length - 1;
while (left <= right) {
int middle = left + (right - left) / 2;
// Check if x is present at mid
if (arr[middle] == target)
return middle;
// If x greater, ignore left half
if (arr[middle] < target)
left = middle + 1;
// If x is smaller, ignore right half
else
right = middle - 1;
}
// if we reach here, then element was
// not present
return -1;
}
public static void main(String[] args) {
int[] arr = { 10, 13, 24, 35, 46, 57, 68 };
int target = 68;
int res = binarySearch(arr, target);
if (res == -1) {
System.out.println("Element not found");
} else {
System.out.println("Element found at index " + res);
}
}
}

You can also try this code with Online Java Compiler
Output
Element found at index 6

You can also try this code with Online Java Compiler
This is the code for binary search, which follows the divide and conquer approach. The algorithm’s running time is proportional to the number of times N can be divided by 2.
Therefore, the time complexity of this algorithm will have a Logarithmic, i.e., O(log n).
Example 5
public class QuickSort {
public static int partition(int[] x, int i, int j) {
int left = i, right = j - 1, pivot = j, complete = 0, t;
while (complete != 1) {
while (x[left] <= x[pivot] && pivot != left)
left++;
if (pivot != left) {
t = x[pivot];
x[pivot] = x[left];
x[left] = t;
pivot = left;
} else
complete = 1;
if (complete != 1) {
while (x[right] >= x[pivot] && pivot != right)
right--;
if (pivot != right) {
t = x[pivot];
x[pivot] = x[right];
x[right] = t;
pivot = right;
} else
complete = 1;
}
}
return pivot;
}
public static void quicksort(int[] x, int i, int j) {
int pivot;
if (i < j) {
pivot = partition(x, i, j);
quicksort(x, i, pivot - 1);
quicksort(x, pivot + 1, j);
}
}
public static void main(String[] args) {
int[] arr = {31, 11, 61, 52, 65, 16, 5, 21, 7, 10};
int len = arr.length;
quicksort(arr, 0, len - 1);
for (int i = 0; i < len; i++)
System.out.print(arr[i] + " ");
}
}

You can also try this code with Online Java Compiler
Output
5 7 10 11 16 21 31 52 61 65
The above example is the logic of the QuickSort algorithm which also follows the divide and conquer approach, just like Binary search, but here, we repeat the iteration N times.
Hence time complexity will be n*log( n ).
Read More - Time Complexity of Sorting Algorithms and Euclid GCD Algorithm
Frequently Asked Questions
What is the difference between Space and Time Complexity?
Time complexity is the amount of time the code is required to be executed. Whereas space complexity is the amount of space needed by the code.
Rank the following by growth rate: n, 2 log n, log n, log (log n), log2 n, (log n) log n, 4, (3/2)^n, n! ?
Rank in increasing order of growth rate is 4, log (log n), log n, log2 n, (log n)log n, 2 log n, n, n!, (3/2)^n.
Which algorithm is better, one having time complexity O(2n) or one having time complexity O(n!)?
O(n!) grows much faster than O(2n). Also, we can see this from the graph given. Thus an algorithm with O(2n) time complexity is much better than an algorithm with factorial time complexity.
Conclusion
This blog has discussed how time complexity deals with the time required to execute a program. We learned to compute time complexity and how important it is to keep in mind to write good code.
Check out this article - Balanced Parentheses
Also, don’t forget to practice the wide variety of DSA problems frequently asked in interview rounds readily available on Code360.