Introduction
Let's begin with understanding the task first. Suppose there is a programming problem that asks you to print the top view of a binary tree. For example, consider the following binary tree-
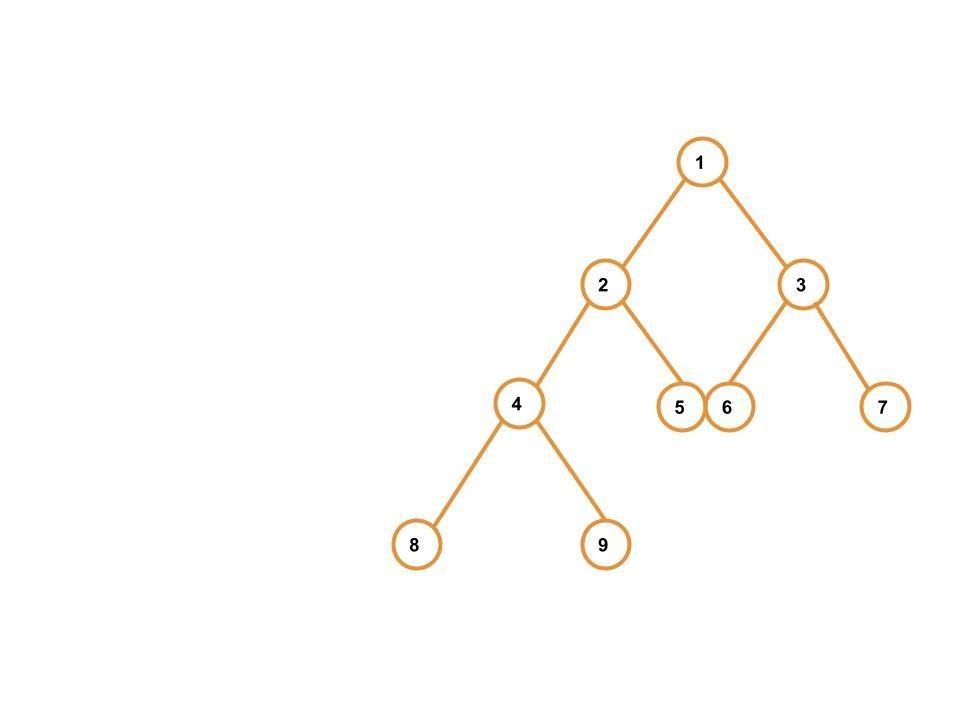
Now, if you print the top view of a binary tree, you will get the following output-
8 4 2 1 3 7
So, we can say that, in the simplest words, the top view of a binary tree refers to the set of nodes visible if we view the tree from an axis parallel to the levels of the tree. Or if we take the topmost nodes of all the vertical orders in it. Vertical orders refer to the set of nodes at a particular horizontal distance.
Though there are various methods to print the top view of a binary tree, we will start with discussing the basic method, which does the level order traversal of the binary tree and prints all the topmost nodes for each value of the horizontal distance. Then move on to advanced methods like two-variable methods etc.
Recommended: Try the Problem yourself first before moving on to the solution.
Basic Approach
This method does find vertical orders in the tree with the help of the horizontal distance of each node, the horizontal distance of the left child of a node is one less than the parent, and the right child is one more than the parent.
Now we do the level order traversal of the tree to ensure that nodes appear in the top to bottom order for every vertical order, and we maintain a hashmap to keep track of the visited nodes for each vertical order.
Algorithm for a basic approach
- Create a binary tree or take it from user input.
- Create a queue to hold nodes during the level order traversal of the tree.
- Create a map to keep track of the visited nodes.
- Start the level order traversal of the binary tree by pushing the root and its horizontal distance into the queue.
- Now run a loop while the queue is not empty-
- Check if the map has a node at that horizontal distance; if not, push it into the map.
- Push the left and right child of the node in the queue, and update the value of their horizontal distance.
- Pop the element from the queue.
- Repeat step 5 at the front of the queue.
- Then print the values on the map.
Implementation of the basic approach
#include <bits/stdc++.h>
using namespace std;
struct node
{
int data;
int hordist;
struct node *left, *right;
};
//To create a new node for the binary tree.
node *createnode(int data)
{
node *var = new node;
var->data = data;
var->left = var->right = NULL;
return var;
}
//Function, which takes the root node of the binary tree
//as argument and prints its top view.
void printtopview(node* root)
{
//base case.
if(root==NULL)
{
return;
}
//Queue to store nodes during level order traversal
//of the tree.
queue<node*> que;
//Map to take horizontal distance and node as key
//value pairs.
map<int, int> mp;
int hordist=0;
root->hordist=hordist;
//Level order traversal of the binary tree.
que.push(root);
while(que.size())
{
hordist=root->hordist;
//If the map has no visited node for that
//horizontal distance, push the node in the map.
if(mp.count(hordist)==0)
{
mp[hordist]=root->data;
}
//Continue the traversal by pushing the left anf
//right nodes into the queue, with the updated
//value of their horixzontal distance.
if(root->left)
{
root->left->hordist=hordist-1;
que.push(root->left);
}
if(root->right)
{
root->right->hordist=hordist+1;
que.push(root->right);
}
que.pop();
root=que.front();
}
//To print the top view of a binary tree.
for(auto itr=mp.begin();itr!=mp.end();itr++)
{
cout<<itr->second<<" ";
}
}
//Driver function.
int main()
{
//Creating the binary tree.
node *root=createnode(1);
root->left=createnode(2);
root->right=createnode(3);
root->left->left=createnode(4);
root->left->right=createnode(5);
root->right->left=createnode(6);
root->right->right=createnode(7);
root->left->left->left=createnode(8);
root->left->left->right=createnode(9);
//Function Call.
printtopview(root);
return 0;
}
Output-
8 4 2 1 3 7
Time Complexity: The time complexity of this approach is O(N*logN), an insertion in a map takes O(logN) time, and we had N nodes to process.
Space Complexity: The space complexity of this approach is O(N).




