Transpose of a Matrix

The Transpose of a Matrix

A transpose of a given matrix is created by inverting the original matrix diagonally.

In other words, a matrix's rows become the transpose's columns, and its columns become the transpose's rows.

The transpose of the matrix is the new matrix created by swapping the rows and columns of the original matrix. If A = [aij] is a m x n matrix, then A's transpose is the matrix obtained by interchanging the rows and columns of A. Transpose of the Matrix is denoted by A’ or (A)^T.

Example:

It would look like this for a two-dimensional square matrix.

Order of Transpose Matrix

One can represent the order of a matrix by the number of rows and columns of a matrix. The vertical lines of the matrix are known as the columns of the matrix, which is represented by m, and the horizontal lines of the matrix are known as the rows of the matrix, which is characterised by n.

They represent the order of a matrix, which is expressed as n x m when put together. And the order of the supplied matrix's transpose is described as m x n.

​Let's revisit our previous example to better grasp how to find a matrix's transpose.

We can see here the given matrix A is of Order 2 x 3 since A contains two rows and 3 Columns. Also, the order of the Transpose of matrix A is 3 x 2.

Properties of Transpose of a Matrix

The transpose of a matrix is employed in various linear transformations because it reveals some of the transformation's significant features. Let's look at some of the very essential aspects of the transpose of a matrix:

Transpose of The Transpose of a Matrix

Two transpose matrix results in the matrix itself: A = (A^T)^T. 

As an example,

The transpose of matrix A, i.e., (A)^T

Again finding the transpose of the matrix, (A^T)^T.

Therefore, it is verified that  (A^T)^T = A.

Transpose of Scalar Multiple

When we first multiply a matrix by a constant(k) and then finds its transpose, It will be equal to k times the Transpose of that matrix, i.e., (kA)^T = kA^T

Let’s see the given an example,
  and K = 2.

We have to Prove that  (kA)^T = kA^T

For the Left-hand side: (kA)^T

Now for the Right-hand Side: kA^T

We find that LHS = RHS, Therefore  (kA)^T = kA^T.

Transpose of Sum

The Sum of the Transpose of two matrices is equal to the transpose of their sum matrix:( A + B )^T = A^T + B^T

Consider the given Example:

Now for  A^T + B^T

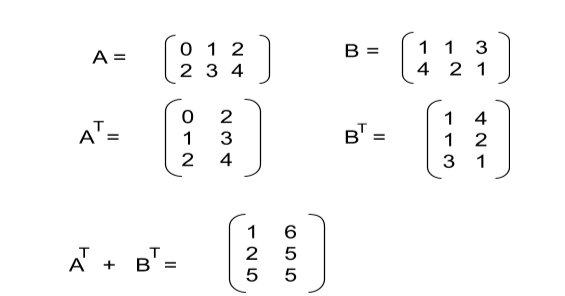
We can see that the Left-hand side is equal to the Right-hand side.

Therefore ( A + B )^T = A^T + B^T is proved.

Note: This property is valid for subtraction also. So, ( A 士 B )^T = A^T 士  B^T.

Transpose of Product

When we find the transpose of the product of two matrices, it will be equivalent to the product of their individual transposes but in a reversed manner.

That is (AB)^T = B^T A^T

To prove this, let us consider an example:

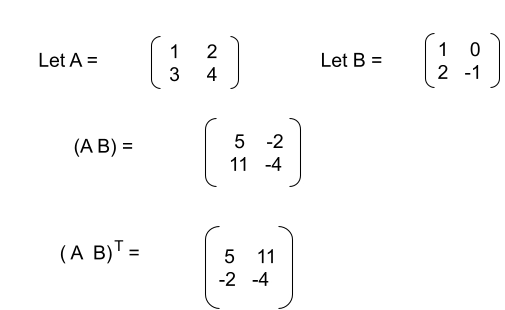
  Now for the expression B^T A^T

Therefore it is proved that  (AB)^T = B^T A^T.

Note: This property is applicable for the product of multiple matrices also. For example, (A B C)^T = C^T B^T A^T.

Check out this problem - Matrix Median

FAQs

1. Where is the transpose of matrix used?
   When we have numerous matrices, and their dimensions are not accessible to multiplication without transposing, we employ transpose.
    
2.  Does transposing a matrix change its determinant?
   No, transposing a matrix does not change its determinant. Using induction, we can also prove it.
    
3. Are transpose and inverse of the matrix the same? 
   No, If you have a matrix A, the transpose A^T is the matrix where the rows and columns are swapped. The matrix inverse A^-1 is the matrix that must be multiplied by matrix A to obtain the identity matrix.
    
4. What is a Skew-Symmetric Matrix?
   When the transpose of a square matrix A of order n x n equals its negative( B^T = -B), it is termed a skew-symmetric matrix. 
    
5. What is an Orthogonal Matrix?
   For a Square matrix A of order n x n, If A^T x A = A x A^T = I, where I is an Identity Element, the matrix is said to be Orthogonal Matrix.

Key Takeaways

This article gives a quick recap of the Introduction to the matrix, its elements, and Dimensions. The transpose of the matrix, Properties of transpose likeTranspose of the Transpose matrix, Transpose of a scalar multiple, transpose of Submission and Subtraction, Transpose of the product of matrix, etc have been discussed in detail.

We hope this blog has helped you.

You can also visit this link to learn about Data interpolation helpful for your aptitude and basic mathematics.

To make your learning more enjoyable, Visit Coding Ninjas Studio, our practice platform, to practice top problems, take mock tests, read interview experiences, and many more technical kinds of stuff.

We wish you Good Luck! Keep coding and keep reading Ninja!!