Types of Matrix

Introduction

If you are preparing for any competitive exam or general school or college level exam, there is a direct question on the types matrix. 

Sometimes you can solve a question directly if you know the type of matrix given and its properties otherwise, the question becomes very lengthy, thus enhancing the chance of a mistake.

You will have a crystal clear idea about every matrix type with proper explanation and examples in this blog. So without wasting any further time, let’s move on with our topic.

Explanation of Types of Matrix

There are many types of matrices available we will discuss every one of them here:

Row Matrix

As the name suggests, the matrix with only one row and more than one number of columns is known as a row matrix. Thus any matrix A=[a_ij]_mxn is said to be a row matrix when m=1.

So we can represent the row matrix as [a_ij]_1xn, and the order of the matrix will be 1 x n.

Example

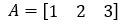
In the above example, A is a row matrix with order 1x3.

Column Matrix

As the name suggests, the matrix with only one column and more than one number of rows is known as a column matrix. Thus any matrix A=[a_ij]_mxn is said to be a row matrix when n=1.

So we can represent the row matrix as [a_ij]_mx1, and the order of the matrix will be m x 1.

Example

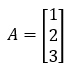
In the above example, A is a column matrix with order 3x1.

Null or Zero Matrix

The matrix which has all the elements as zero is known as the zero matrix. It is denoted by 0.

[aij]mxn is said to be a zero matrix when aij = 0 for all values of i and j. In this, the order doesn’t matter. It can be of any order, just one condition that all elements inside the matrix must be zero.

Example

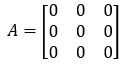
We have a matrix with order 3x3 as a zero matrix in the above example.

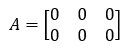
We have a matrix with order 2x3 as a zero matrix in this example.

Singleton Matrix

The matrix that contains only one element is a singleton matrix. With one element, we are referring to a matrix with only one row and one column. So [a_ij]_mxn  in a standard matrix m=1, n=1. The order of a singleton matrix will be one.

Example 

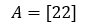
Here A contains only one element; hence it is a singleton matrix.

Horizontal Matrix

The matrix that contains more columns than the number of rows is called a horizontal matrix.

In terms of the order, if a matrix has an order of m x n, then n>m.

Example

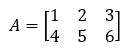
Here A is a horizontal matrix as it has more columns than rows.

Vertical Matrix

The matrix that contains more rows than the number of columns is called a vertical matrix.

In terms of the order, if a matrix has an order of m x n, then m>n.

Example

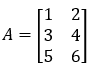
Here A is a vertical matrix as it has more rows than columns.

Square Matrix

The matrix that contains the same number of rows as that of columns is called a square matrix.

A= [a_ij]_mxn is said to be a square matrix if m=n.

Example

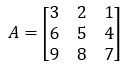
A is a matrix with order 3 x 3. A is a square matrix as the number of rows = the number of columns.

Diagonal Matrix

In a diagonal matrix, when we say diagonal, we mean principal diagonal.

A matrix with zero elements except the diagonal elements is called a diagonal matrix.

There is some condition that a matrix should follow to be called a diagonal matrix, and these are:

1. The given matrix should be a square matrix, i.e., the number of rows should be the same as the number of columns.
2. All the elements except the elements from the principal diagonal must be zero.

Example

Here A is a diagonal matrix of order 3x3 as it is a square matrix, and all the elements except the principal diagonal are zero.

Scalar Matrix

It is an extension of a diagonal matrix. A matrix that obeys all the conditions of the diagonal matrix and all the elements along the principal diagonal are equal is called a scalar matrix.

Let’s understand this with an example:

Example

Here A is a diagonal matrix with all principal diagonal elements equal.

Identity or Unit Matrix

Unit matrix is also an extension of the diagonal matrix. A matrix that follows all the diagonal matrix conditions and has all the principal diagonal elements 1 is called an identity or unit matrix.

We can have some conclusions regarding the unit matrix.

1. All identity matrices are scalar matrices.
2. All scalar matrices are diagonal matrices.
3. All diagonal matrices are square matrices.

Example

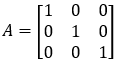
Here A is a diagonal matrix with all principal diagonal elements as one.

Equal Matrices

Two matrices are said to be equal when they follow some conditions.

1. The number of rows of both the matrices should be identical.
2. The number of columns of both the matrices should be identical.
3. All the elements corresponding to the same positions must be equal.

When two matrices that satisfy all of the above conditions are called equal matrices.

An important point to remember here is that we are not talking about order to be equal. Here we are talking about the number of rows and columns to be equal individually.

Example

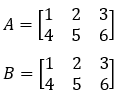
Here A and B are two different matrices with the same number of rows and columns, and all the elements corresponding to the same positions are equal.

Triangular Matrix

When a square matrix has all the elements above or below the principal diagonal as zero, the rest have values known as the triangular matrix.

There are two types of triangular matrices

1. Upper Triangular Matrix

The square matrix with all the elements below the principal diagonal as zero is called the upper triangular matrix.

Example

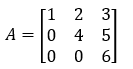
Here A is a square matrix, and all the elements below principal diagonals are zero.

2. Lower Triangular Matrix

The square matrix with all the elements above the principal diagonal as zero is called the lower triangular matrix.

Example

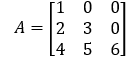
Here A is a square matrix, and all the elements above principal diagonals are zero.

Singular Matrix

When the determinant of a square matrix is zero, it is called a singular matrix.

Example

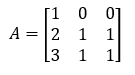
If you find the determinant of A, it will be zero hence it is a singular matrix.

Non-Singular Matrix

When the determinant of a square matrix is not equal to zero, it is called a non-singular matrix.

Example

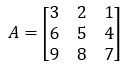
If you find the determinant of A, you will find it is not zero; hence it is a non-singular matrix.

Symmetric Matrix

A square matrix A = [aij ] is said to be symmetric if aij = aji for all values of i and j. In this, the transpose of A should be equal to it.

Example

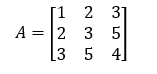
Here A holds the condition for symmetric matrix.

Skew-Symmetric Matrix

A square matrix A = [aij ] is symmetric if aij = -aji for all values of i and j and all the principal diagonal elements are zero. In this, A's transpose should be equal to the negative of the primary matrix.

Example

Here A satisfies the condition of a skew-symmetric matrix.