Introduction
UGC NET or NTA-UGC-NET is the examination for determining the eligibility for the assistant professor and/or Junior Research Fellowship award in Indian universities and colleges. National Testing Agency examines on behalf of the University Grants Commission. In this article, we will cover the first 25 questions. We have covered questions 26 to 50 in the second part of UGC NET Nov 2017 PAPER-II Part-2.
1. If the time is now 4 O’clock, what will be the time after 101 hours from now?
(1) 9 O’clock
(2) 8 O’clock
(3) 5 O’clock
(4) 4 O’clock
Answer: (1) 9 O’clock
Explanation: After 96 hours, it is 4 o'clock as it is divisible by 24, and after 5 hours, it is 9 o'clock. (96+5=101)
2. Let m=(313)4 and n=(322)4. Find the base 4 expansion of m+n.
(1) (635)4
(2) (32312)4
(3) (21323)4
(4) (1301)4
Answer: (4) (1301)4
Explanation: (313)=3*16+4*1+3=55;
(322)=3*16+4*2+2=58;
The sum is 55+58=113.
113 in base 4 can now be represented as 1301 in base 4.
3.
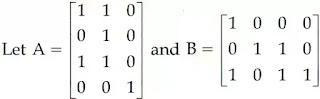
Find the boolean product A⊙B of the two matrices.

(A) (1) (B) (2) (C) (3) (D) (4)
Answer: (A) (1)
Explanation: Only if the number of columns in the first matrix equals the number of rows in the second matrix can we multiply them.
As a result, the boolean product AB is Option 1.
4. How many distinguishable permutations of the letters in the word BANANA are there?
(1) 720
(2) 120
(3) 60
(4) 36
Answer: (3) 60
Explanation: We have six letters in total in BANANA, but we have some duplicate letters as well, therefore we must deal with them and eliminate those duplicate cases.
A – 3 N – 2 B – 1
So the total number of words conceivable is factorial(6), i.e. 6! However, we must delete duplicate words: i.e. (6!/(2!*3!)), which yields 60 distinct permutations of the letters in BANANA.
5. Consider the graph given below:
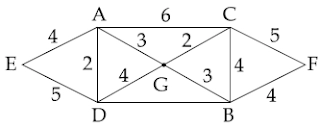
Use Kruskal’s algorithm to find a minimal spanning tree for the graph. The List of the edges of the tree in the order in which they are chosen is?
(1) AD, AE, AG, GC, GB, BF
(2) GC, GB, BF, GA, AD, AE
(3) GC, AD, GB, GA, BF, AE
(4) AD, AG, GC, AE, GB, BF
Answer: Marks to all
Explanation: Kruskal's algorithm is an MST (minimum-spanning-tree) algorithm that discovers the edge with the smallest feasible edge weight that connects any two trees in the forest (initially all vertex are considered as a separate tree). Kruskal's algorithm uses the greedy algorithm approach in graph theory to find an MST for a linked weighted graph by adding increasing cost edges at each step (such that the graph does not form a cycle).
Edges were sorted by weight.
Edge weight
AD 2
GC 2
GB 3
GA 3
BC 4
BF 4
DG 4
AE 4
ED 5
CF 5
AC 6
DB weight not specified
So, in the order of increasing edge weight, the bold edges above will create an MST of the graph.
6. The Boolean function with the Karnaugh map is:
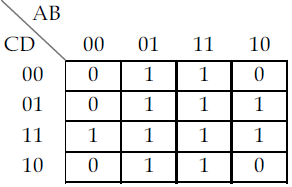
(1) (A+C).D+B
(2) (A+B).C+D
(3) (A+D).C+B
(4) (A+C).B+D
Answer: 1
Explanation:
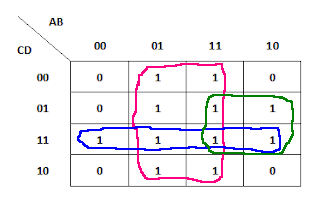
We'll acquire B + CD + AD from the aforementioned Karnaugh map. It can be written as (A+C).D+B
7. The Octal equivalent of the binary number 1011101011 is
(1) 7353
(2) 1353
(3) 5651
(4) 5657
Answer: (2) 1353
Explanation: Starting from the far right, group all the bits in the binary number into groups of three. If you don't have enough numbers to make a set of three, add zeros to the left of the final one.
1011101011 is the original binary code.
1 011 101 011 after grouping
Adding Zeros for Groups of Three: 001 011 101 011
001=1, 011=3, 101=5, 011=3
So the final answer will be 1353.
8. Let P and Q be two propositions, ¬ (P ↔ Q) is equivalent to
(1) P ↔ ¬ Q
(2) ¬ P ↔ Q
(3) ¬ P ↔ ¬ Q
(4) Q → P
Answer: 1,2
Explanation:
P |
Q |
¬P |
¬Q |
Q → P |
⌐(P ↔ Q) |
P ↔ ⌐ Q |
⌐P↔ Q |
⌐P↔ ⌐Q |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
9. Negation of the proposition ∃ x H(x) is :
(1) ∃x ¬ H(x)
(2) ∀ x ¬ H(x)
(3) ∀ x H(x)
(4) ¬ x H(x)
Answer: (2) ∀ x ¬ H(x)
Explanation: Negation of (∃ x H(x)) = ¬ ∃ x H(x) = ∀ x ¬ H(x)(as the negation symbol moves from left to right, the symbol ∃ changes to ∀).
10. The output of the following combinational circuit is F.
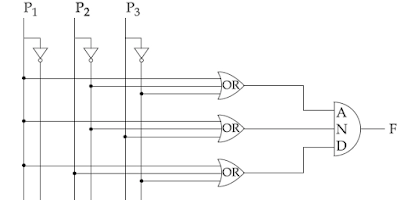
The value of F is :
(1) P1 + P2' P3
(2) P1 + P2' P3'
(3)P1 + P2 P3'
(4)P1'+ P2 P3
Answer: (2) P1+P2'P3'
Explanation: outputs of OR gates are:
(P1+P2'+P3') . (P1+P2'+P3) . (P1+P2+P3')
= (P1+P1P2'+P1P3+P2'+P2'P3+P3'P1+P3'P2+0) . (P1+P2+P3')
=(P1+P1P2'+P1P3+P3'P1+P2'+P2'P3+P3'P2) . (P1+P2+P3')
= (P1+P2') . (P1+P2+P3')
=(P1+P1P2+P1P3'+P2'P1+0+P2'P3')
=(P1+P2'P3')
11. ‘ptrdata’ is a pointer to a data type. The expression *ptrdata++ is evaluated as (in C++) :
(1) *(ptrdata++)
(2) (*ptrdata)++
(3) *(ptrdata)++
(4) Depends on compiler
Answer: (1) *(ptrdata++)
Explanation: because the ++ operator takes precedence over the * operator
12. The associativity of which of the following operators is Left to Right in C++?
(1) Unary Operator
(2) Logical not
(3) Array element access
(4) address of
Answer: (3) Array element access
Explanation: Associativity from right to left with a unary operator
Right-to-left associativity for logical not.
Array element access -- Array subscript - [ ] - Left to Right associativity addressof -- right to left associativity
13. A member function can always access the data in __________ , (in C++).
(1) the class of which it is a member
(2) the object of which it is a member
(3) the public part of its class
(4) the private part of its class
Answer:: (1) the class of which it is a member
Explanation: A member function can access class member variables regardless of the access specifier used to declare the member variable. As a result, a member function can always access the data in the class to which it belongs.
14. Which of the following is not correct for virtual function in C++?
(1) Must be declared in the public section of the class.
(2) Virtual function can be static.
(3) Virtual function should be accessed using pointers.
(4) Virtual function is defined in the base class.
Answer: (2) Virtual function can be static.
Explanation: A virtual function must be declared in the base class's public section and is overridden by the derived class. You can call a virtual function for a derived class object when we refer to it with a reference to the base class. The version of the function defined in the derived class will then be executed.
15. Which of the following is not correct (in C++)?
(1) Class templates and function templates are instantiated in the same way.
(2) Class templates differ from function templates in the way they are initiated.
(3) Class template is initiated by defining an object using the template argument.
(4) Class templates are generally used for storage classes.
Answer: OPTION 2, 3, 4 ARE CORRECT (as per UGC answer key)
Explanation: The way a class template and a function template are begun in C++ is similar. Storage classes do not employ class templates. Class templates and function templates are both instantiated in the same way, and a class template is not started by defining an object with the template.
16. Which of the following is/are true with reference to ‘view’ in DBMS?
(a) A ‘view’ is a special stored procedure executed when a certain event occurs.
(b) A ‘view’ is a virtual table that occurs after executing a pre-compiled query. (1) Only (a) is true
(2) Only (b) is true
(3) Both (a) and (b) are true
(4) Neither (a) nor (b) are true
Answer: (2) Only (b) is true
Explanation: A 'view' is a virtual table, not particular storage. The view is only available after performing a pre-compiled query.
17. In SQL, __________ is an Aggregate function.
(1) SELECT
(2) CREATE
(3) AVG
(4) MODIFY
Answer: AVG
Explanation: The AVG function is used to calculate the average of the values of a specific attribute. For example, to determine the average compensation of a company's employees.
18. Match the following with respect to RDBMS :
(a) Entity Integrity (i) enforces some specific business rules that do not fall into entity or domain.
(b) Domain integrity(ii) Rows that can’t be deleted that are used by other records
(c) Referential integrity(iii) enforces valid entries for a column
(d) User-defined integrity (iv) No duplicate rows in a table
Code :
(1) (iii) (iv) (i) (ii)
(2) (iv) (iii) (ii) (i)
(3) (iv) (ii) (iii) (i)
(4) (ii) (iii) (iv) (i)
Answer: (2) (iv) (iii) (ii) (i)
Explanation: According to Codd's rule, entity integrity must be maintained so that no duplicate records exist in the database.
Column entries in RDBMS tables must be valid; this also falls under Codd's rule.
Referential data items strongly adhere to integrity throughout table insertion, deletion, and modification, and user set integrity constraints to enlist some unique business rules that do not come within entity or domain.
19. In RDBMS, different classes of relations are created using __________ technique to prevent modification anomalies.
(1) Functional Dependencies
(2) Data integrity
(3) Referential integrity
(4) Normal Forms
Answer: (4) Normal Forms
Explanation: To decrease redundancy and improve data consistency, normal forms are utilized.
20. __________ SQL command changes one or more fields in a record.
(1) LOOK-UP
(2) INSERT
(3) MODIFY
(4) CHANGE
Answer: (3) MODIFY
Explanation: In SQL, MODIFY is used to modify records in the db table.
21. Consider an array representation of an n element binary heap where the elements are stored from index 1 to index n of the array. For the element stored at index i of the array (i<=n), the index of the parent is :
(1) floor ((i+1)/2)
(2) ceiling ((i+1)/2)
(3) floor (i/2)
(4) ceiling (i/2)
Answer: (3) floor (i/2)
Explanation: Binary heaps can be represented using arrays, which store elements in an array and use their relative positions inside the array to express child-parent relations.
For the binary heap element placed at index I in the array,
The parent node will be at index: floor(i/2).
Left Child will be at index: 2i
Child will be at index: 2i 2*i + 1
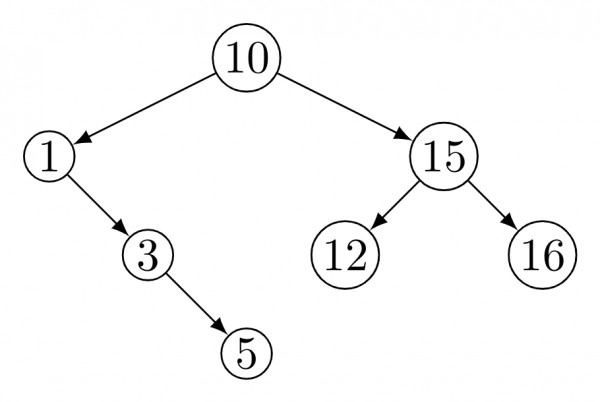
22. The following numbers are inserted into an empty binary search tree in the given order: 10, 1, 3, 5, 15, 12, 16. What is the height of the binary search tree?
(1) 3
(2) 4
(3) 5
(4) 6
Answer: (1) 3
Explanation:
23. Let G be an undirected connected graph with a distinct edge weight. Let Emax be the edge with maximum weight and Emin the edge with minimum weight. Which of the following statements are false?
(1) Every minimum spanning tree of G must contain Emin.
(2) If Emax is in the minimum spanning tree, then its removal must disconnect G.
(3) No minimum spanning tree contains Emax.
(4) G has a unique minimum spanning tree.
Answer: (3) No minimum spanning tree contains Emax.
Explanation: Option an is correct. All MST should include emin.
Option b is correct: if emax is present, it signifies that is the sole edge reachable by one of the incident vertices. Otherwise, we will select a lower weight edge incident on that vertex, therefore removing it will disconnect G.
We cannot conclude whether c and d are always true. They can occasionally be false.
24. A list of n strings, each of length n, is sorted into lexicographic order using merge - sort algorithm. The worst-case running time of this computation is :
(1) O(n log n)
(2) O(n2 log n)
(3) O(n2 + log n)
(4) O(n3)
Answer: (2) O(n2 log n)
Explanation: When sorting an array of n integers, the recurrence relation for the total number of comparisons will be,
T(n) = 2T(n/2) + (n), where (n) is the number of comparisons required to merge two sorted subarrays of size n/2.
= (nlog2n)
Instead of integers, which require O(1) time to compare, we are given n strings. We can compare two strings in O(n) time. As a result, the total number of comparisons will now be (n2log2n), with each comparison taking O(n) time.
Merge sort, in general, does (nlog2n) comparisons and runs in (nlog2n) time if each comparison can be performed in O(1) time.
25. Postorder traversal of a given binary search tree T produces the following sequence of keys : 3, 5, 7, 9, 4, 17, 16, 20, 18, 15, 14. Which one of the following sequences of keys can be the result of an in-order traversal of the tree T?
(1) 3, 4, 5, 7, 9, 14, 20, 18, 17, 16, 15
(2) 20, 18, 17, 16, 15, 14, 3, 4, 5, 7, 9
(3) 20, 18, 17, 16, 15, 14, 9, 7, 5, 4, 3
(4) 3, 4, 5, 7, 9, 14, 15, 16, 17, 18, 20
Answer: (4) 3, 4, 5, 7, 9, 14, 15, 16, 17, 18, 20
Explanation: Because a BST's inorder traverse always returns elements in increasing order. For this question, the in-order tree traversal will always be the sorted order of keys for post-order traversal.
FAQs
What is the purpose of the UGC NET Exam?
UGC NET is an abbreviation for University Grants Commission National Eligibility Test. It is a national-level test used to evaluate eligibility for lectureships and Junior Research Fellowships (JRF) in Indian institutions and colleges.
Can I apply for UGC NET after completing a PG diploma?
A PGDM is equivalent to a master's degree. So, if you hold a PG Diploma from a recognized university, you are eligible to apply for the exam.
What is the minimum age for applying to the UGC NET Exam?
According to the UGC NET Eligibility, there is no age limit for assistant professors, but candidates for JRF must be at least 31 years old.
Will distance learning be accepted for the UGC NET?
Yes, distance education is acceptable for the UGC NET Exam, provided you are enrolled in a UGC accredited university/institute.
What is the UGC NET syllabus?
The NTA administers the UGC NET Exam in two parts: General Paper-1 (common to all topics) and Paper-2 (subject-specific). The syllabus for each Paper 2 subject varies. You can view the entire UGC NET Syllabus.




