UGC NET June 2015 Paper-II Part-1

Introduction

UGC NET Exam is a very popular exam in India for people interested in research. Solving Previous Year Questions are an excellent way to learn about the exam pattern and practice for it. By solving the PYQs, you will get a basic idea about your preparation. In this article, we have given the questions of UGC NET 2015 June Paper-II. We have also explained every problem adequately to help you learn better.

Note: This article contains Q.No. 1 to Q.No. 25 out of the 50 questions asked in NET June 2015 paper II. The solutions to Q.No. 26 to Q.No. 50 can be found in June 2015 Paper-II Part-2 article.

June 2015 Paper-II

1. How many strings of 5 digits have the property that the sum of their digits is 7 ?
   (A) 66  (B) 330
   (C) 495   (D) 99
   Answer: B
   There should be string with 5 digits and sum of those digits should be 7.
   The starting digit of any string should not be 0 and we also have to consider the repetition of digits.
   Example of such strings are 70000,61000,60100,60010,.....
   The total possible number of strings can be found out by using permutations and combinations by considering the different cases.
   So the possible number of strings are ^n+r-1C_r-1
   In this question, n=7 and r=5, ^n+r-1C_r-1 = ¹¹C₄ = 330
   Also read, permutation of string
2. Consider an experiment of tossing two fair dice, one black and one red. What is the probability that the number on the black die divides the number on red die ?
   (A) 22 / 36      (B) 12 / 36
   (C) 14 / 36      (D) 6 / 36
   Answer: C
   Total possible ways when throwing two fair dice= 6*6= 36
   Possibe cases where number on one die divides the number on another die= (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,2), (2,4), (2,6), (3,3), (3,6), (4,4), (5,5), (6,6)
   Total number of ways= 14
   Therefore, probability= 14/36
3. In how many ways can 15 indistinguishable fish be placed into 5 different ponds, so that each pond contains at least one fish ?
   (A) 1001                     (B) 3876
   (C) 775           (D) 200
   Answer: A
   We know that the number of ways to distribute ‘n’ items in ‘r’ different groups where each must get at least 1 is ^n-1C_r-1.
   As per question, n=15, r=5.
   Therefore ^n-1C_r-1 = ¹⁴C₄ = 1001
4. Consider the following statements:
   (a) Depth - first search is used to traverse a rooted tree. 
   (b) Pre - order, Post-order and Inorder are used to list the vertices of an ordered rooted tree.
   (c) Huffman's algorithm is used to find an optimal binary tree with given weights.
   (d) Topological sorting provides a labelling such that the parents have larger labels than their children.
   Which of the above statements are true ?
   (A) (a) and (b)            (B) (c) and (d)
   (C) (a) , (b) and (c)    (D) (a), (b) , (c) and (d)
   Answer: D
   Depth-first search is a traversing algorithm where it explores one node and its children as far as possible and then it reverts back to explore another node. It can be used for trees, graphs, etc.
   Pre-order, post-order, and Inorder are traversing techniques where all the nodes are traversed from the root node in a tree.
   An optimal binary tree generates a Huffman code using Huffman's algorithm.
   In topological sorting, labels are provided on the basis of the number of edges heading towards that node. If the number of edges is less then it will have a higher priority. We know that there is an edge directed from the parent node to the children node. So the priority of the parent node will be higher than the children node.
   So, all the statements are true.
5. Consider a Hamiltonian Graph (G) with no loops and parallel edges. Which of the following is true with respect to this Graph (G) ?
   (a) deg(v) ≥ n/2 for each vertex of G
   (b) |E(G)| ≥ 1/2 (n-1)(n-2)+2 edges
   (c) deg(v) + deg(w) ≥ n for every v and w not connected by an edge
   (A) (a) and (b)            (B) (b) and (c)
   (C) (a) and (c)            (D) (a), (b) and (c)
   Answer: C
   Dirac’s theorem on Hamiltonian cycles states that an n-vertex graph in which each vertex has a degree of at least n/2 must have a Hamiltonian cycle. So, (a) is true.
   Ore’s theorem states that if deg(v) + deg(w) >=n for every pair of distinct non-adjacent vertices v and w of G, then G is Hamiltonian. Here deg(v) denotes the number of edges in G to v. So, (c) is true.
   A complete graph of n vertices has n(n-1)/2 edges and a hamiltonian cycle in G contains n edges. Therefore the maximum number of edge-disjoint hamiltonian cycles can not exceed (n-1)/2. So, (b) is false.
6. Consider the following statements :
   (a) Boolean expressions and logic networks correspond to labelled acyclic digraphs.
   (b) Optimal Boolean expressions may not correspond to simplest networks.
   (c) Choosing essential blocks first in a Karnaugh map and then greedily choosing the largest remaining blocks to cover may not give an optimal expression.
   Which of these statement(s) is/ are correct?
   (A) (a) only                 (B) (b) only
   (C) (a) and (b)            (D) (a), (b) and (c)
   Answer: D
   An acyclic digraph is a directed graph containing no directed cycles which is called DAG(Directed Acyclic Graph). We can represent the boolean expressions and logic networks by using DAG. And it is not necessary that the optimal boolean expressions always correspond to the simplest networks. So, (a) and (b) are true.
   Karnaugh maps reduce logic functions more quickly and easily compared to boolean algebra but a greedy approach in K-map may not always work. So, (c) is also ture.
7. Consider a full-adder with the following input values:
   (a) x=1, y=0 and Ci(carry input) = 0
   (b) x=0, y=1 and Ci = 1
   Compute the values of S(sum) and C0 (carry output) for the above input values.
   (A) S=1 , C0= 0 and S=0 , C0= 1     (B) S=0 , C0= 0 and S=1 , C0​= 1
   (C) S=1 , C0= 1 and S=0 , C0​= 0     (D) S=0 , C0= 1 and S=1 , C0​= 0
   Answer: A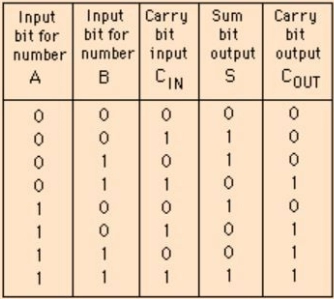
   
   Source
   We can see from the above table that x=1, y=0, C_in=0 implies that S=1 and C_out=0.
   And when x=0, y=1, C_in=1 implies that S=0 and C_out=1.
   For the given x and y values, the correct option is A
8. "lf my computations are correct and I pay the electric bill, then I will run out of money. If I don't pay the electric bill, the power will be turned off. Therefore, if I don't run out of money and the power is still on, then my computations are incorrect."
   Convert this argument into logical notations using the variables c, b, r, p for propositions of computations, electric bills, out of money and the power respectively. (Where  ¬ means NOT)
   (A) if (c∧b) → r and ¬b → ¬p, then (¬r∧p)→¬c
   (B) if (c∨b) → r and ¬b → ¬p, then (r∧p)→c
   (C) if (c∧b) → r and ¬p → ¬b, then (¬r∨p)→¬c
   (D) if (c∨b) → r and ¬b → ¬p, then (¬r∧p)→¬c
   Answer: A
   (c^b) means my computations are correct and I pay the electricity bill.
   (¬r^p) means I don’t run out of money and the power is still on.
   According to the statement, option A is correct.
9. Match the following:
   List - I                                  List - II
   (a) (p →q) ⇔ (¬q→¬p)         (i) Contrapositive
   (b) [(p∧q)→r]⇔[p→ (q→r)]   (ii) Exportation law
   (c) (p→q)⇔[(p∧¬q)→o]        (iii) Reductio ad absurdum
   (d) (p⇔q)⇔[(p→q)∧(q→p)]    (iv) Equivalence 
   Codes:
   (a) (b) (c) (d)
   (A)  (i) (ii) (iii) (iv)
   (B)  (ii) (iii) (i) (iv)
   (C)  (iii) (ii) (iv) (i)
   (D)  (iv) (ii) (iii) (i)
   Answer: A
   The contrapositive is an inference that says that a conditional statement is logically equivalent to its contrapositive. In contrapositive, the antecedent and its consequent both are inverted and flipped, i.e., (p →q) ⇔ (¬q→¬p).
   Exportation law states that “if (P and Q), then R” is equivalent to “if P then (if Q then R)”. This can be logically expressed as [(p∧q)→r]⇔[p→ (q→r)].
   Reductio ad absurdum is a technique to expose the fallacy.
   The equivalence rule translates into “if and only if” and is symbolized by “⇔”
10. Consider a proposition given as:
    "x≥6, if x² ≥ 5 and its proof as:
    If x≥6, then x² = x.x ≥ 6.6 = 36 ≥ 25
    Which of the following is correct w.r.to the given proposition and its proof ?
    (a) The proof shows the converse of what is to be proved.
    (b) The proof starts by assuming what is to be shown.
    (c) The proof is correct and there is nothing wrong.
    (A) (a) only     (B) (c) only
    (C) (a) and (b)   (D) (b) only
    Answer: C
    The proof described in question is wrong as it is mentioned x² >= 5 but in proof it is mentioned 36 >= 25 which is wrong.
11. What is the output of the following program ?
    (Assume that the appropriate pre-processor directives are included and there is no syntax error)
    main()
    {
    char S[ ] = "ABCDEFGH";
    printf ("%C",* (& S[3]));
    printf ("%s", S+4);
    printf ("%u", S);
    /* Base address of S is 1000 */          
    }
    (A) ABCDEFGH1000           (B) CDEFGH1000
    (C) DDEFGHH1000             (D) DEFGH1000
    Answer: D
    printf ("%C",* (& S[3])) prints the character at index 3, i.e., ‘D’
    printf ("%s", S+4) prints the string starting from index (0+4), i.e., “EFGH”
    printf ("%u", S) prints the address of starting index, i.e., “1000”
12. Which of the following, in C++, is inherited in a derived class from base class ?
    (A) constructor          (B) destructor
    (C) data members     (D) virtual methods
    Answer: C
    Data members are inherited in a derived class from the base class. A derived class can access all non-private members of its base class.
13. Given that x=7.5, j=-1.0, n=1.0, m=2.0
    the value of --x+j == x>n>=m is:
    (A) 0    (B) 1
    (C) 2    (D) 3
    Answer: A
    The order of performing the operations is to be taken care of in this question
    First, we perform the pre-decrement and addition operation.
    --x+j = --(7.5) + (-1.0) = 6.5 - 1.0 = 5.5
    Note that after this operation, the value of x has become 6.5 from 7.5
    Now, the expression becomes
    (5.5) == 6.5 > 1.0 >= 2.0
    Now, all the operators have an equal preference so perform the operations in left to right order. We get zero as the final answer.
14. Which of the following is incorrect in C++ ?
    (A) When we write overloaded function we must code the function for each usage.
    (B) When we write function template we code the function only once.
    (C) It is difficult to debug macros
    (D) Templates are more efficient than macros
    Answer: None of these
    In this question all the given options are correct. So, marks were given to all.
15. When the inheritance is private, the private methods in base class are.................. in the derived class (in C++).
    (A) inaccessible        (B) accessible
    (C) protected             (D) public
    Answer: A
    A derived class can access the public and protected members but not the private members. Private members can only be accessed by the same class.
16. An Assertion is a predicate expressing a condition we wish database to always satisfy. The correct syntax for Assertion is :
    (A) CREATE ASSERTION ‘ASSERTION Name’ CHECK ‘Predicate’
    (B) CREATE ASSERTION ‘ASSERTION NAME’
    (C) CREATE ASSERTION, CHECK Predicate
    (D) SELECT ASSERTION
    Answer: A
    An Assertion is a condition we wish the database always satisfies. Domain constraints, functional dependencies, and referential integrity are special forms of assertion. The syntax of Assertion in SQL is:
    CREATE ASSERTION ‘ASSERTION Name’ CHECK ‘Predicate’
17. Which of the following concurrency protocol ensures both conflict serializability and freedom from deadlock ?
    (a) 2-phase Locking
    (b) Time stamp - ordering
    (A) Both (a) and (b)  (B) (a) only
    (C) (b) only                 (D) Neither (a) nor (b)
    Answer: C
    2-phase locking provides a schedule that is conflict serializable but not free from deadlock. Time stamp ordering provides both conflict serializability and freedom from deadlocks.
18. Drop Table cannot be used to drop a Table referenced by .................. constraint.
    (a) Primary key          (b) Sub key    (c) Super key         (d) Foreign key
    (A) (a)              (B) (a), (b) and ©
    (C) (d)             (D) (a) and (d)
    Answer: C
    Drop-Table cannot be used to drop a Table referenced by a Foreign Key constraint because deleting a table referenced by a foreign key will violate the referenced key constraint.
19. Database applications were built directly on top of file system to overcome the following drawbacks of using file-systems
    (a) Data redundancy and inconsistency
    (b) Difficulty in accessing Data
    (c) Data isolation
    (d) Integrity problems
    (A) (a)                       (B) (a) and (d)
    (C) (a), (b) and (c)     (D) (a), (b), (c) and (d)
    Answer: D
    The file system has some drawbacks like Data redundancy, data inconsistency, difficulty in accessing data, data isolation, and integrity problems. These problems were solved by using the database as it uses some specific constraints to overcome each of these problems. The constraints that help overcome these problems in databases are 
    Entity constraint: No NULL values in the primary key
    Key constraint: No two rows should be same in a table
    Domain constraint: A column should not be multi-valued or composite.
    Referential integrity: Foreign key should contain the subset values of the primary key.
20. For a weak entity set to be meaningful, it must be associated with another entity set in combination with some of their attribute values, is called as :
    (A) Neighbour Set    (B) Strong Entity Set
    (C) Owner entity set (D) Weak Set
    Answer: C
    A weak entity set does not have any primary key using which we can identify it uniquely. So to identify it uniquely, it must be associated with its owner entity set and must have total participation with its owner entity set.
21. Consider the given graph:
    
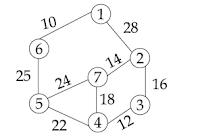
    Its Minimum Cost Spanning Tree is .................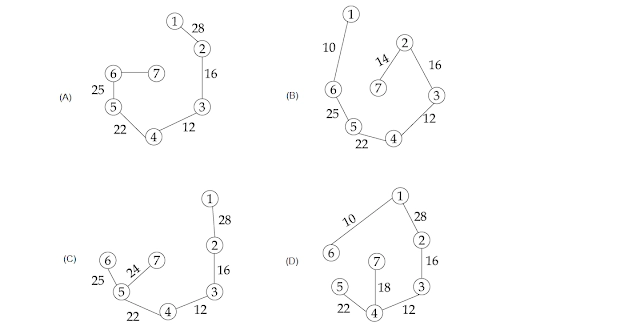
    
    Answer: B
    To find a minimum cost spanning tree, we can use Prim’s algorithm or Kruskal’s algorithm. In Prim’s algorithm, first, we connect the nodes having the minimum weighted edge to connect to the existing spanning tree. Then that node gets connected to the spanning tree, and all the nodes connected to that node are then considered to be attached to the current spanning tree. This process repeats till all the nodes are attached to the spanning tree.
22. The inorder and preorder Traversal of binary Tree are dbeafcg and abdecfg respectively. The post-order Traversal is ............
    (A) dbefacg                (B) debfagc
    (C) dbefcga                (D) debfgca
    Answer: D
    Pre-order traversal: Root -> Left -> Right
    Post-order traversal: Left -> Right -> Root
    In-order traversal: Left -> Root -> Right
    Using the given in-order and pre-order traversal we can construct the binary tree as given below.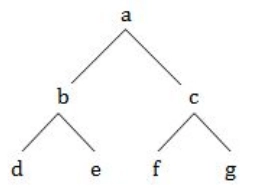
    
    So, the post-order traversal of the given binary tree is “ebfgca”.
23. Level order Traversal of a rooted Tree can be done by starting from root and performing:
    (A) Breadth First Search     (B) Depth first search
    (C) Root search                    (D) Deep search
    Answer: A
    Breadth-First Search is an algorithm for traversing. In this, we start at the root, explore all of its neighbor nodes at the present depth, and then move on to the nodes at the next depth level. So this traversing algorithm is the most suitable for level order traversal.
24. The average case occurs in the Linear Search Algorithm when:
    (A) The item to be searched is in some where middle of the Array
    (B) The item to be searched is not in the array
    (C) The item to be searched is in the last of the array
    (D) The item to be searched is either in the last or not in the array
    Answer: A
    In Linear Search algorithm all the elements are traversed from starting to end till the element is found. Worst case occurs when the target element lies in the end as it has to perform ‘n’ number of comparisons. Best case occurs when target element is in the starting position as it has perform only ‘1’ comparison. Average case occurs when the number of comparisons is around ‘n/2’, i.e., the target element lies somewhere in the middle of the array.
25. To determine the efficiency of an algorithm the time factor is measured by:
    (A) Counting micro seconds
    (B) Counting number of key operations
    (C) Counting number of statements
    (D) Counting kilobytes of algorithm
    Answer: B
    To determine the efficiency of an algorithm, the time factor is measured by counting the number of key operations performed.