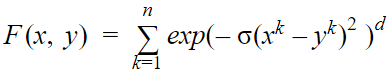Understanding the idea behind Kernels

Introduction

 

The kernel is essentially a function to perform calculations even in the higher dimensions. We use Kernels in SVM to reduce the complexity of calculations. A Kernel can do calculations for an even infinite number of dimensions.

 

As the dimensions increase in SVM, it becomes difficult to form a HyperPlane, so we have to resort to Kernels to form a hyperplane.

 

Check out this link to learn more about Support Vector Machine in detail. 

 

Kernel Trick

 

With the help of kernel functions, we can calculate the high dimensional relationships without actually transforming the data to the higher dimension; this trick to get the high dimensional intuition is known as the Kernel Trick.

 

With the help of the kernel trick, we can reduce the amount of computation power required for SVMs because we don’t have to do the math to transform the data into a high dimension.

 

Example:

 

The picture below shows us the data, which is currently in one dimension. There are two classes (green and red) in the dataset that we have to segregate.

Source: StatQuest youtube channel

 

It is linearly impossible to separate the two classes in one dimension; hence we use the kernel trick that gives us the intuition that we are working with 2-Dimensional data.

 

Now, it is easier to segregate the classes linearly.

 

Types of SVM Kernels

 

Linear Kernel

 

The most basic type of Kernel is a linear kernel. It is mainly preferred for classification problems where the variables can be linearly separated.

 

Formula:

 

Where x and y represent the data, we’re trying to classify.

 

Polynomial Kernel

 

The polynomial kernel is primarily used in Image Processing tasks. The polynomial kernel is less accurate and less efficient than other kernels functions in SVM.

 

Formula:

 

Gaussian kernel

 

We use the Gaussian Kernel function when we don’t know the data or the data is unexplored. The Gaussian kernel is a widely and most commonly used kernel function.

 

Formula:

 

 

Gaussian radial basis function (RBF)

 

The Gaussian radial basis kernel or RBF for short is also used where we don’t have any prior knowledge of the dataset. We generally use RBF for a non-linear dataset.

 

Formula:

 

Here the lies between [0, 1].

 

Laplace RBF kernel

 

Laplace RBF kernel is another modification of the RBF kernel. We use this general-purpose kernel when the provided dataset is un-explored.

 

Formula:

 

 

Hyperbolic tangent kernel

 

In the Neural Networks tasks, the Hyperbolic Tangent kernel is preferred.

 

Formula:

 

 

Sigmoid kernel

 

We primarily use the sigmoid kernel as a proxy for the Neural Networks. The sigmoid kernel function is similar to a two-layer perceptron model that works as an activation function for the neurons.

 

Formula:

 

 

ANOVA kernel

 

The ANOVA kernel is mainly used in regression-related problems. The performance of the ANOVA kernel is good for multi-dimensional regression tasks.

 

Formula: