Union and Intersection of Two Linked Lists

Introduction

This blog will discuss the various approaches to solving the Union and the Intersection of two Linked Lists. Before jumping into the problem of getting the Union and Intersection of two Linked Lists, let’s first understand a Linked list.

A Linked list is a kind of data structure in which the elements are connected using pointers, and each node has the address of the pointer of its next node.

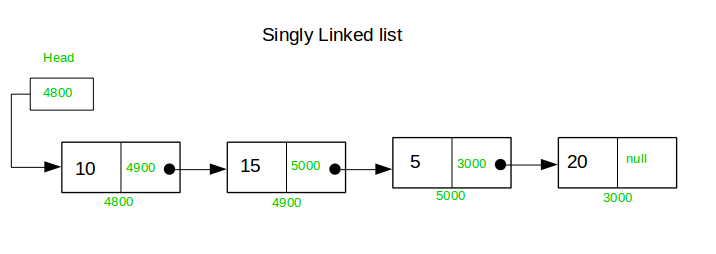
You can refer to this link for more information on the linked list.

In this Union and Intersection of two Linked Lists problem, we need to return the head of the linked list after taking the union and intersection of two linked lists regardless of the order of the nodes in the linked list.

Note: Duplicates are not present in the same linked list.

For Example:-

List1 :- 10 -> 15 -> 45 -> 17 -> 145 

List2 :- 145 -> 5 -> 11 -> 45 -> 43 -> 1 

Union List :-  45 -> 15 -> 10 -> 17 -> 145 -> 145 -> 45 -> 11 -> 5 -> 43 -> 1 -> 75 

Intersection List :- 145 -> 45

Brute Force Approach

Brute Force Solution considers traversing the ‘list2’ and checking each element with an element of ‘list 1’, if the same element is present, then we just have to add that element in the intersection list, whereas, for the union list, we just need to add all the elements of ‘list1’ in union list, and when traversing the ‘list2’, if that particular element is already present in ‘list1’, then skip that element and if that element is not present in the ‘list1’ then we just need to add that element in the union list.

Algorithm for Union 

Step 1. Create a function ‘getUnion()’ that will accept two parameters, i.e., one head pointer of the linked list 1, one head pointer of the linked list 2.

Step 2. Initialize a resultant union list ‘unionList’ with a NULL value, and two variables ‘temp1’ with the head of linked list1 and ‘temp2’ with the head of linked list2.

Step 3. Make an iteration using the ‘while’ loop to traverse linked list 1 with the help of ‘temp1’, which will terminate when ‘temp1’ is equal to the NULL value.

Step 4. Create a function ‘helper’ to push all the given elements in the given ‘head’ of the linked list, and with the help of this ‘helper’ function, we have to push all the nodes during the iteration.

Step 5. Assign the value of the pointer of the ‘next’ node of ‘temp1’ to ‘temp1’.

Step 6. Make an iteration using the ‘while’ loop to traverse linked list 2 with the help of the ‘temp2’, which will terminate when ‘temp2’ is equal to the NULL value.

Step 7. Create a boolean function ‘present’, which will take two parameters, one will be the head of the resultant ‘UnionList’, and the other will be the data of that respective ‘temp2’ which we need to check.

Step 8. Check if the node of the same data is already present in the resultant linked list or not using the ‘present’ function.

• If it is not present, then we need to push the same element in the resultant ‘unionList’ linked list using the ‘helper’ function.

Step 9. Assign the value of the pointer of the next node of the ‘temp2’ to ‘temp2’.

Step 10. Return the pointer of the head of the resultant ‘UnionList’ linked list.

Algorithm for Intersection

Step 1. Create a function ‘getIntersection()’ that will accept two parameters, i.e., one head pointer of the linked list 1, one head pointer of the linked list 2.

Step 2. Initialize a resultant intersection list ‘intersectionList’ with a NULL value, and two variable ‘temp’ with the head of linked list1.

Step 3. Make an iteration using the ‘while’ loop to traverse linked list 1 with the help of ‘temp1’, which will terminate when ‘temp1’ is equal to the NULL value.

Step 4. Check with the help of the ‘present’ function, if the element of the same value is present in the other linked list or not.

• If it is present, then push that element in the resultant ‘intersectionList’ using the ‘helper’ function.

Step 5. Assign the value of pointer of next node of ‘temp’ to ‘temp’

Step 6. Return the pointer of the head of ‘intersectionList’.

Implementation in C++

#include <bits/stdc++.h>

using namespace std;

// Linked list's node's structure
struct Node {
    int data;
    struct Node * next;
};

// Add node to the list
void push(struct Node ** head_ref, int new_data) {
    struct Node * new_node = (struct Node * ) malloc(sizeof(struct Node));

    // Insert Data
    new_node -> data = new_data;

    // Link it with the list
    new_node -> next = ( * head_ref);

    // Increment the head pointer
    ( * head_ref) = new_node;
}

// Check the presence of the data
bool present(struct Node * head, int data) {
    struct Node * temp = head;
    while (temp != NULL) {
        if (temp -> data == data)
            return 1;
        temp = temp -> next;
    }
    return 0;
}

/* Function to get union of two
linked lists head1 and head2 */
struct Node * getUnion(
    struct Node * head1,
    struct Node * head2) {
    struct Node * result = NULL;
    struct Node * t1 = head1, * t2 = head2;

    // Insert all elements of
    // list1 to the result list
    while (t1 != NULL) {
        push( & result, t1 -> data);
        t1 = t1 -> next;
    }

    // Insert those elements of list2
    // which are not present in result list
    while (t2 != NULL) {
        if (!present(result, t2 -> data))
            push( & result, t2 -> data);
        t2 = t2 -> next;
    }
    return result;
}

/* Function to get intersection of
two linked lists head1 and head2 */
struct Node * getIntersection(struct Node * head1, struct Node * head2) {
    struct Node * result = NULL;
    struct Node * temp1 = head1;

    // Traverse the first linked list
    while (temp1 != NULL) {
        if (present(head2, temp1 -> data))
            push( & result, temp1 -> data);
        temp1 = temp1 -> next;
    }
    return result;
}

// Print the linked list
void printList(struct Node * node) {
    while (node != NULL) {
        cout << " " << node -> data;
        node = node -> next;
    }
}

int main() {

    // Empty list
    struct Node * head1 = NULL;
    struct Node * head2 = NULL;
    struct Node * intersectionList = NULL;
    struct Node * unionList = NULL;

    // First Linked List
    push( & head1, 10);
    push( & head1, 15);
    push( & head1, 45);
    push( & head1, 17);
    push( & head1, 145);

    // Second Linked List
    push( & head2, 145);
    push( & head2, 5);
    push( & head2, 11);
    push( & head2, 45);
    push( & head2, 43);
    push( & head2, 1);

    intersectionList = getIntersection(head1, head2);
    unionList = getUnion(head1, head2);
    cout << "Given First linked list:-";
    printList(head1);
    cout << endl;
    cout << "Given Second linked list:-";
    printList(head2);
    cout << endl;
    cout << "Intersection Linked list:-";
    printList(intersectionList);
    cout << endl;
    cout << "Union linked list:-";
    printList(unionList);
    cout << endl;
}

You can also try this code with Online C++ Compiler

Run Code

Output :

Given Linked List1:- 10 -> 15 -> 45 -> 17 -> 145 
Given Linked List2:- 145 -> 5 -> 11 -> 45 -> 43 -> 1 
Union:-  45 -> 15 -> 10 -> 17 -> 145 -> 145 -> 45 -> 11 -> 5 -> 43 -> 1 -> 75 
Intersection:- 145 -> 45

Complexity Analysis

Time Complexity: O(M * N) 

As we are working on two linked lists of sizes ‘M’ and ‘N’ respectively, and for both union and intersection, we are comparing each element of a linked list with the complete other linked list, therefore, the overall time complexity will be O(M * N). 

Space Complexity: O(N)

As we are using constant space, therefore, the overall space complexity will be O(1).