Introduction
Viterbi algorithm is a very nice solution for one of the Hidden Markov model problems, in which we have to find the hidden state while the observable state is already given. On the other hand, the Markov Model or the Markov process is a memoryless change in eventless. We will understand how to use Markov models to decode Viterbi.
Viterbi Decoding with Hidden Markov Models
The Viterbi calculation is unique programming for acquiring the most excellent deduced likelihood gauge of the most probable grouping of stowed away states called the Viterbi way that outcomes in an arrangement of noticed occasions, particularly with regards to Markov data sources and secret Markov models (HMM).
Understanding Viterbi Algorithm
A Viterbi decoder involves the Viterbi calculation for translating a bitstream encoded utilizing a convolutional or lattice code.
There are different calculations for translating a convolutionally encoded stream (for instance, the Fano calculation). The Viterbi estimate is the most asset-consuming, yet it does the greatest probability interpreting. It is most frequently utilized for translating convolutional codes with limitation lengths k≤3, yet esteems up to k=15 are being used.
Viterbi translating was created by Andrew J. Viterbi and distributed in the paper Viterbi, A. (April 1967). "Mistake Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm." IEEE Transactions on Information Theory.
There is both equipment (in modems) and programming executions of a Viterbi decoder.
Formula to find the states that maximize the conditional probability of any given data:
X*0:T = argmax X0:TP[X0:T|Y0:T]Understanding HMM
A secret Markov model is a Markov chain for which the state is just to some degree recognizable or uproariously noticeable. Perceptions are connected with the condition of the framework, yet they are generally deficient to precisely decide the state. A few notable calculations for buried Markov models exist. For instance, given a succession of perceptions, the Viterbi analysis will process the most probable comparing arrangement of states, the forward calculation will register the likelihood of the grouping of perceptions, and the Baum-Welch measure will appraise the beginning probabilities, the progress work, and the perception capacity of a secret Markov model.
One regular use is for discourse acknowledgment, where the noticed information is the discourse sound waveform, and the secret state is the verbally expressed text. The Viterbi calculation observes the most probable grouping of spoken words given the discourse sound in this model.
Documentation and definitions
A secret Markov model is a probably generative robot that creates an arrangement while navigating through a limited engagement of states. An HMM is characterized by an assortment of boundaries: a beginning state I, a bunch of progress boundaries (an ij ), and a bunch of outflow boundaries (b I (c)). Let m be the number of states. A way π through the HMM is an arrangement of conditions π0 = I, π1, π2, ..., π n with the end goal that for all i 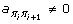 , For every way π of length n + 1 the likelihood that this way radiates grouping.
, For every way π of length n + 1 the likelihood that this way radiates grouping.
x = x1x2 ... x n is 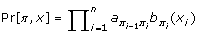 . The Viterbi calculation tracks down the most plausible way through the HMM for a given grouping. The normal execution of the Viterbi calculation utilizes dynamic programming to build a Θ(mn) measured grid, in which cells compare to state-position sets. There is a characteristic expansion to tracking down the k-best ways in the HMM: store the k most important scoring ways for each position-state pair. The k most elevated likelihood ways for x1... x I that end in-state π I should be from the k-best ways to every one of the states for the grouping from x1 to xi-1. This perception prompts a Viterbi-like calculation with runtime k times as enormous and requiring Θ(km) stockpiling. This approach has been utilized in discourse acknowledgment as soon as the 1990s. However, its space prerequisites make it infeasible for tracking down the k-best ways for huge upsides of k on significant HMMs for long groupings.
. The Viterbi calculation tracks down the most plausible way through the HMM for a given grouping. The normal execution of the Viterbi calculation utilizes dynamic programming to build a Θ(mn) measured grid, in which cells compare to state-position sets. There is a characteristic expansion to tracking down the k-best ways in the HMM: store the k most important scoring ways for each position-state pair. The k most elevated likelihood ways for x1... x I that end in-state π I should be from the k-best ways to every one of the states for the grouping from x1 to xi-1. This perception prompts a Viterbi-like calculation with runtime k times as enormous and requiring Θ(km) stockpiling. This approach has been utilized in discourse acknowledgment as soon as the 1990s. However, its space prerequisites make it infeasible for tracking down the k-best ways for huge upsides of k on significant HMMs for long groupings.
Then again, finding the k-best ways, however, an HMM should be visible as tracking down k most straightforward ways in a diagram with nm hubs (one for each position-state pair). The chart has O(m2n) edges, each edge relating to likely progress between HMM states. On this diagram, one can apply Eppstein's calculation to track down k most limited ways in O(m2n + k) time. This calculation keeps the entire Θ(m2n)- size chart in memory and a Ω(mn) size structure utilized in the computation; it additionally has high consistent variables in the runtime and certainly addresses the ways.
A space reserve funds approach for Viterbi was introduced by Sramek et, which utilizes a compacted tree way to deal with effectively free memory involved by superfluous back pointers in the state-position framework. We make an m by n + 1 network of hubs where every hub compares to a cell of the Viterbi framework (a position-state pair): every section relates to them potential decisions for the last state in a prefix of x. We make an edge between hub v I of segment I and hub v I +1 of section I + 1 if the Viterbi way to the position-state pair (I + 1, vi+1) goes through v I. Edges give the back pointers in the robust programming for the Viterbi computation. Assuming we eliminate all hubs and rims that are not on ways from section n of the diagram to state I in segment 0, a tree remains. In the methodology of Sramek et al., this tree is effectively pruned, and hubs with precisely one parent are converged into their folks as they are made.
Registering the probabilities
To register the k most elevated way probabilities to each state at the position I, we accept that we have an arranged rundown of the k-best way probabilities to each state at the place I - 1. Then, at that point, assuming we are thinking about an express a whose potential ancestors in the HMM are Pred(a), we can find the k-best probabilities for express an at position I by playing out an activity the same as the principal k advances we would attempt in blending |Pred(a)| records for mergesort. The Viterbi likelihood of the ℓ-the best way to state v is:
max cePred(v) (Pr acvbv(xi))We can register this amount in O(m) time per way; it is a fascinating algorithmic inquiry whether this can be accelerated heuristically, since all ways to state v that were in state c at the position I - 1 will have their probabilities increased by a similar steady, a cv b v (x I ).
Then, this computation takes k times the expense of a standard Viterbi estimation and Θ(mk) space. Conversely, the back calculations yielding non-zero likelihood ways of Fariselli et al. and Kall et al. run asymptotically as quickly as Viterbi. However, produce just a solitary path, which might be by and large an odd one from a naturally visible view.
Putting away and pruning the ways
The k best ways can be registered by utilizing a three-layered network, where passage (I, j, a) relates to the a th best way to state j for succession x1, ..., x I. Regarding this network as a diagram, we draw an edge from (I, j, a) to (I + 1, k, b) if the b th best way to state k at the position I + 1 purposes the a th best way to state j at position I. As in the Viterbi calculation, we wish to effectively keep up with just the passages in the chart that compare to ways to the current boondocks, position I of the succession.
We will portray two sorts of hubs in the chart: way hubs, which relate to a solitary worth of (I, j, a), and state hubs, which compare to all ways (I, j, a) where I and j are kept consistent. An edge between two state hubs exists on the off chance that any of their way hubs have an advantage.
Pruning and compressing details
Assume we are going to incorporate succession letter, x i. We ascertain the probability of all k most ideal ways to each state. If the ℓ-th best way to state c purposes way hub (i', b, a) at the previous advance (where i' want not to be i - 1 because of compression), then, at that point, we set that hub to be the parent of (i, c, ℓ), updating the child counters for (i', b, a). We also set the state hub (i', b) as a child to have (i, c).
After performing this arrangement of operations for all the new diagram hubs corresponding to succession position i (at all states), we prune all corners not reachable from the fresh leaves by seeing which leaves at level i - 1 are as of now not accessible. For every way hub in this "evacuation list", we eliminate the way hub from its state hub and update appropriate counters. If its parent's child counter arrives at nothing, it is also moved to the evacuation list. If a way hub eliminated was the last way hub for that state hub, then, at that point, the state hub is taken out. We likewise identify if a state hub enters the condition that it has just a single child and its child has just that one parent: if thus, the states are combined.
Since this algorithm is done online, the active footprint of memory utilized by the algorithm is dramatically not exactly Θ(kmn) in practice. However, it might be that enormous in outrageous cases.
Recovering the ways
We should separate the k ways with the highest probability whenever we have delivered the final construction. The k way possibilities at every one of them leaves are the probabilities of the best practices to those states. We select the k of highest chance from these km ways, as the first k strides of a m-way mergesort, in O(km) time, and we develop the k-best ways than in O(kn) time after the merging. The naive algorithm's total run time is O(nm2k), as the upward in doing the ways compression is more modest than the basic calculations. The is no assurance that the new strategy is more space-efficient: our heuristic may not generally bring about a reduction.
Memory and runtime
Our algorithms dramatically diminish the memory utilization of finding the k best ways in this HMM. Above is shown the maximum memory required in decoding the 45 proteins with a signal peptide for additional upsides of k: while these qualities in all actuality do develop with k, the memory use for the tree-based approach is approximately fifty times less than for the naive methodology; it accepts twice as much memory as a methodology that just registers the probabilities and doesn't store back pointers by any means. We note that we might have involved the naive algorithm in the memory footprint of a typical PC in this application. Be that as it may, we figured out the 10 000 best ways for the double geography proteins described underneath, which could never have been possible with the naive algorithm.
Final Understanding
We have fostered a memory-efficient algorithm for finding k-best ways in an HMM. Considering the k best ways of an HMM is not novel; discourse recognition specialists have considered the idea. Previous algorithms for this have either utilized a lot of memory or been heuristic in nature. Our technique has a significantly lower memory footprint in practice than the naive implementation. Using this algorithm, we investigated the utilization of k-best ways in geography prediction for transmembrane proteins. While better than the Viterbi algorithm, forming an agreement of the k-best ways doesn't proceed as well as the 1-best algorithm; to a great extent, the issue is finding the right by and large geography, which 1-best improves, possibly for training reasons. Where the k-best ways give the by and large right geography, we can quite often process a decent agreement prediction. We can separate other exciting information from the k-best ways. In particular, we can estimate our confidence in a forecast by looking at the substance and probability distribution of the k-best ways. Finally, we have shown that in the particular instance of double geography proteins, simple processing of the k-best ways can regularly predict both of the suitable topologies of a protein.




