Introduction
Today, let's learn about a famous and commonly asked Interview Problem, i.e., the ZigZag Traversal of a Binary Tree.
So, Binary Tree is a generic tree with only two children, i.e., left and right. And ZigZag Traversal of a Binary Tree here means that we need to print the nodes in the given tree in a zigzag manner, i.e., from left to right for the first level, then right to left for the next level and so on, following alternate directions for alternate levels.
Problem Statement: Given the root of the binary tree, we need to return the zigzag level order traversal of its nodes' values.
Example:
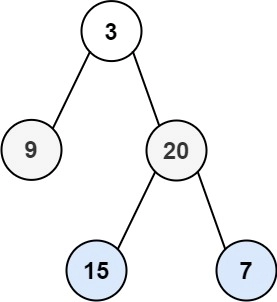
So, here we would first print the root (3) and then traverse right to left and print [20,9] and then finally traverse left to right printing [15,7], completing the ZigZag traversal of Binary Tree.
Let's get started and learn various approaches to solving this problem.
Recommended: Do try the Problem by yourself first before moving on to the solution.
Approach - Using Two Stacks
We could achieve ZigZag traversal of Binary Tree by having 2 stacks(Stack - A LIFO data structure) for alternate (left to right) and (right to the left) traversal and then print the nodes alongside.
So,
Step1: We create 2 stacks of type TreeNode. Initially, stack1 stores the root, and stack2 is empty.
We work till both the stacks are not empty.
We then enter inside the loop where we perform the following steps:
-
While (Stack1’s size() > 0)
- The popped node’s Right Child (Rc) is entered in stack2 and printed if it exists.
- The popped node’s Left Child (Lc) is entered in stack2 and printed if it exists.
-
While (Stack2’s size() > 0)
- The popped node’s Left Child (Lc) is entered in stack1 and printed if it exists.
- The popped node’s Right Child (Rc)is entered in stack1 and printed if they exist.
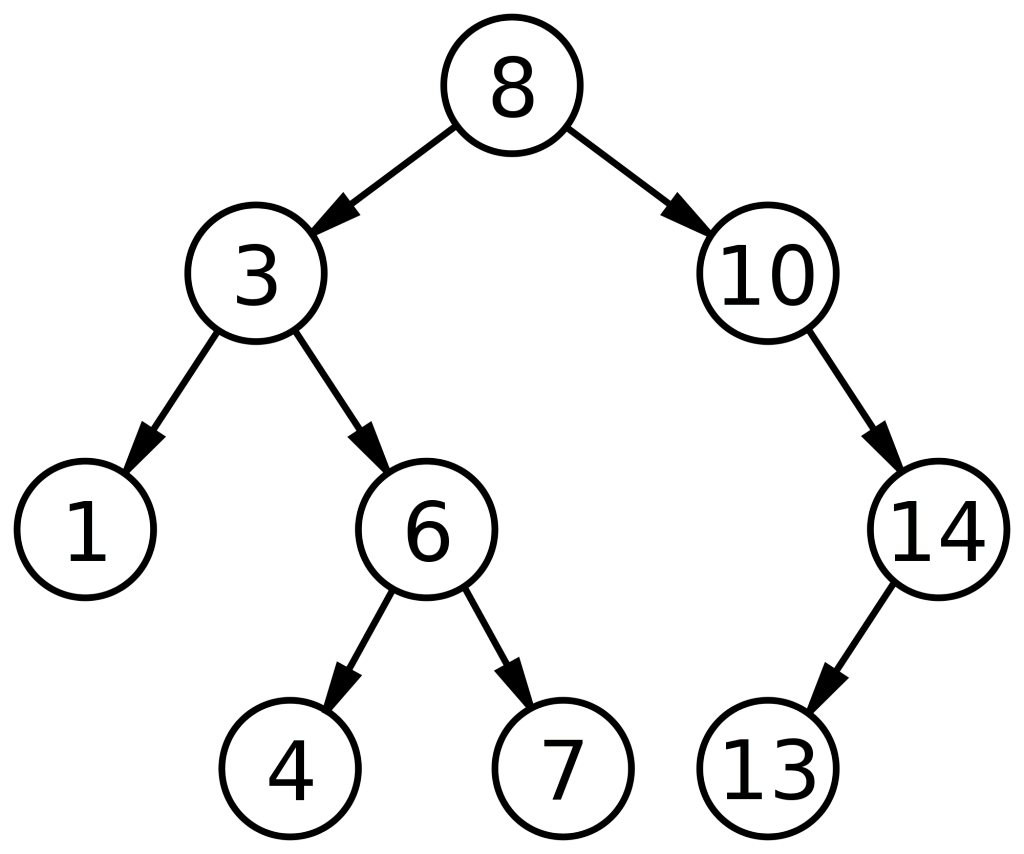
Let us do a dry run on this tree for a better understanding:
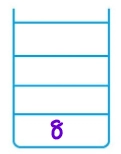
Stack1 - [8] Stack2 - [ ]. Also, Root ie 8 is printed.

We enter the while loop:
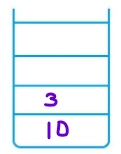
- So, 8 is popped from Stack1 and its Rc(10) and Lc(3) are added in Stack2.
Stack1 =[] Stack2 = [3, 10] and 10 3 are printed.

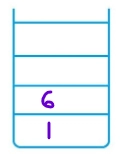
2. So, 3 is popped from Stack2, and its Lc(1) and Rc(6) are added in Stack1.
Stack1 =[6,1] Stack2 = [10] and 1 6 are printed.
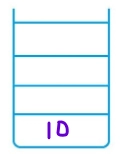
3. 10 is popped from Stack2 and its Rc(14) is added in Stack1. (Lc of 10 does not exist).
Stack1 =[14, 6,1] Stack2 = [ ] and 14 is printed.
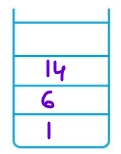

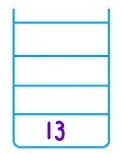
4. Similarly, 14 is popped from Stack1, and its Rc(13) is added in Stack2. (Lc of 14 does not exist).
Stack1 =[6,1] Stack2 = [13] and 13 is printed.
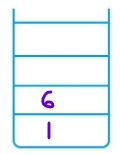
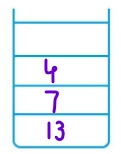
5. 6 is popped from Stack1 and its Rc(7) and Lc(4) are added in Stack2.
Stack1 =[1] Stack2 = [4,7,13] and 7, 4 are printed.
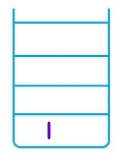
6. 1 is popped from Stack1. Lc and Rc of 1 do not exist.
Stack1 =[] Stack2 = [4,7,13]

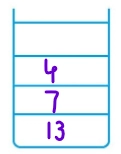
7. 4 is popped from Stack2. Lc and Rc of 4 do not exist.
Stack1 =[] Stack2 = [7,13]

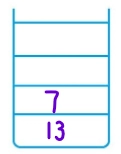
8. 7 is popped from Stack1. Lc and Rc of 7 do not exist.
Stack1 =[] Stack2 = [13]

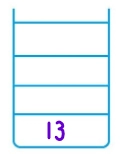
9. 13 is popped from Stack1. Lc and Rc of 13 do not exist.
Stack1 =[] Stack2 = []
Since both the stacks are empty, the loop ends.


Implementation-
Let’s have a look at its implementation in Java -
import java.util.*;
import java.lang.*;
import java.io.*;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class Solution {
public static void zigzagLevelOrder(TreeNode root) {
System.out.println("ZigZag traversal of Binary Tree: ");
// Creating 2 stacks to store alternate levels
Stack<TreeNode> stack1 = new Stack<>();
Stack<TreeNode> stack2 = new Stack<>();
// When a node is added, it is printed too.
stack1.push(root);
System.out.println(root.val);
while (stack1.size() > 0 || stack2.size() > 0){
//Stack1's elements are removed and its children are added into stack2
//in form - Rc Lc(Right child and Left child)
while (stack1.size() > 0){
TreeNode currNode = stack1.pop();
if (currNode.right != null){
System.out.print(currNode.right.val + " ");
stack2.push(currNode.right);
}
if (currNode.left != null){
System.out.print(currNode.left.val + " ");
stack2.push(currNode.left);
}
System.out.println();
}
//Stack2's elements are removed and its children are added into stack1
//in form Lc Rc(Left cild and Right child)
while (stack2.size() > 0){
TreeNode currNode = stack2.pop();
if (currNode.left != null){
System.out.print(currNode.left.val + " ");
stack1.push(currNode.left);
}
if (currNode.right != null){
System.out.print(currNode.right.val + " ");
stack1.push(currNode.right);
}
System.out.println();
}
}
}
public static void main (String[] args) {
Scanner s = new Scanner(System.in);
System.out.println("Form a tree: ");
TreeNode root = new TreeNode(s.nextInt());
root.left = new TreeNode(s.nextInt());
root.right = new TreeNode(s.nextInt());
root.right.left = new TreeNode(s.nextInt());
root.right.right = new TreeNode(s.nextInt());
zigzagLevelOrder(root);
}
}
Output:
Form a tree: 3 9 20 15 7
ZigZag traversal of Binary Tree:
3
20 9
15 7
Time and Space Complexity
Time Complexity: O(n) as we are traversing all the nodes of the Binary tree in ZigZag traversal of Binary Tree at least once.
Space Complexity: O(n) as extra space for storing the nodes of alternate levels in the stack has been used.
Where n is the number of nodes in a Binary Tree.





