Last Updated: 23 Jul, 2021
Bellman Ford
Moderate
Asked in companies



You have been given a directed weighted graph of ‘N’ vertices labeled from 1 to 'N' and ‘M’ edges. Each edge connecting two nodes 'u' and 'v' has a weight 'w' denoting the distance between them.
Your task is to calculate the shortest distance of all vertices from the source vertex 'src'.
Note:
If there is no path between 'src' and 'ith' vertex, the value at 'ith' index in the answer array will be 10^8.
Example :
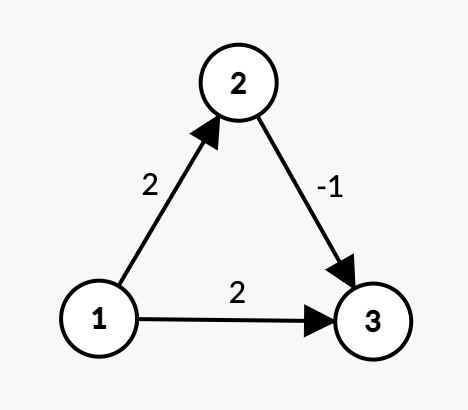
3 3 1
1 2 2
1 3 2
2 3 -1
In the above graph:
The length of the shortest path between vertex 1 and vertex 1 is 1->1 and the cost is 0.
The length of the shortest path between vertex 1 and vertex 2 is 1->2 and the cost is 2.
The length of the shortest path between vertex 1 and vertex 3 is 1->2->3 and the cost is 1.
Hence we return [0, 2, 1].
Note :
It's guaranteed that the graph doesn't contain self-loops and multiple edges. Also, the graph does not contain negative weight cycles.
Input Format :
The first line contains three single space-separated integers ‘N’, ‘M’, and ‘src’ denoting the number of vertices, the number of edges in the directed graph, the source vertex, respectively.
The following ‘M’ lines contain three single space-separated integers ‘u’, ‘v’, and ‘w’, denoting an edge from vertex ‘u’ to vertex ‘v’, having weight ‘w’.
Output Format :
Return an integer denoting the shortest path length from ‘src’ to ‘dest’. If no path is possible, return 10^9.
Note :
You do not need to print anything; it has already been taken care of. Just implement the given function.
Approaches
In this algorithm, we have a source vertex and we find the shortest path from source to all the vertices.
For this, we will create an array of distances D[1...N], where D[i] stores the distance of vertex ‘i’ from the source vertex. Initially all the array values contain an infinite value, except ‘D[source]’, ‘D[source]’ = 0.
The algorithm consists of several iterations and in each iteration, we try to produce relaxation in the edges. Relaxation means reducing the value of ‘D[i]’.
For this, we will iterate on the edges of the graph let’s consider an edge (‘u’, ’v’, ’w’) :
- If ‘D[v]’ is greater than ‘D[u]’ + ‘w’, then ‘D[v]’ = ‘D[u]’ + ‘w’.
The algorithm claims that ‘N-1’ iterations are enough to find the distances of the vertices from the source vertex.
We also know that the graph doesn’t contain negative weight cycles. Hence we do not need to check it explicitly.
Algorithm:
- Make an array ‘D’ and initialize the array with an infinite value, except ‘D[source]’, ‘D[source]’ = 0.
- Do ‘N’ - 1 iterations and in each iteration follow the below steps:
- Iterate on the edges on the graph and for each edge (‘u’,’v’,’w’) update the value to ‘D[v]’, i.e., ‘D[v]’ = min(‘D[v]’, ‘D[u]+w’).
- Return the value of ‘D[‘dest’]’.

