BST Iterator

You are given a class named as BSTIterator that represents an iterator over inorder traversal of a binary search tree. You need to implement the following things as follows:

1. BSTIterator(Node root) - It is a parameterized constructor in which you are given the root of the Binary search tree. It will be called whenever an object of BSTIterator is created.

2. next() - This member function will return the next smallest element in the in-order traversal of the binary search tree. You need to implement this function.

3. hasNext() - This function will return true if there exists the next smallest element in the traversal else it will return false. You need to implement this function

The binary search tree has ‘N’ nodes you need to print the inorder traversal of the tree using the iterator.

Input Format:

The first line of the input contains an integer ‘T’ denoting the number of test cases.

The first and the only line of each test case contains elements of the tree in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.

For example, the input for the tree depicted in the below image would be :

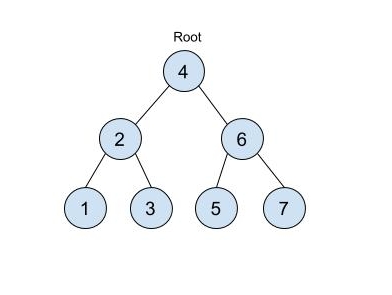
4
2 6
1 3 5 7
-1 -1 -1 -1 -1 -1

Explanation :

Level 1 :
The root node of the tree is 4

Level 2 :
Left child of 4 = 2
Right child of 4 = 6

Level 3 :
Left child of 2 = 1
Right child of 2 = 3
Left child of 6 = 5
Right child of 6 = 7

Level 4 :
Left child of 1 = null (-1)
Right child of 1 = null (-1)
Left child of 3 = null (-1)
Right child of 3 = null (-1)
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.

The input ends when all nodes at the last level are null(-1).

Note :

The above format was just to provide clarity on how the input is formed for a given tree.

The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

4 2 6 1 3 5 7 -1 -1 -1 -1 -1 -1

Output Format:

The single line of output for each test case should contain the inorder traversal of the binary search tree.

Note:

You do not need to print anything, it has already been taken care of. Just implement the given function.

Constraints:

1 <= T <= 10
1 <= N <= 10^4  
1 <= A[i] <= 10^9 

Where ‘T’ is the number of test cases, ‘N’ is the number of nodes, and A[i] is the value of a node.

Time Limit: 1 sec