Last Updated: 10 Nov, 2020

Fix BST

Hard

Asked in companies

Solve now

Problem statement

You have been given a Binary Search Tree of 'N' nodes, where exactly two nodes of the same tree were swapped by mistake.

Your task is to restore or fix the BST, without changing its structure and return the root of the corrected BST.

Note:

Given BST will not contain duplicates.

Example

A Binary Search Tree (BST) whose 2 nodes have been swapped is shown below.

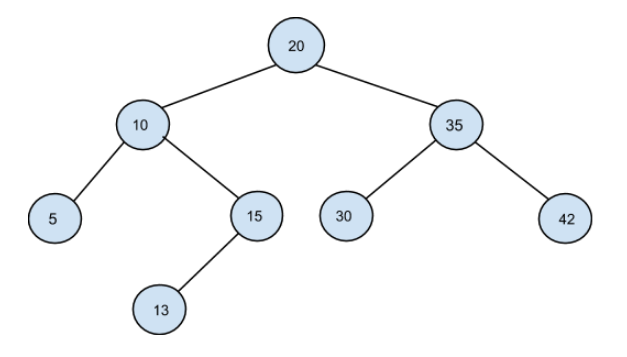
example

After swapping the incorrect nodes:

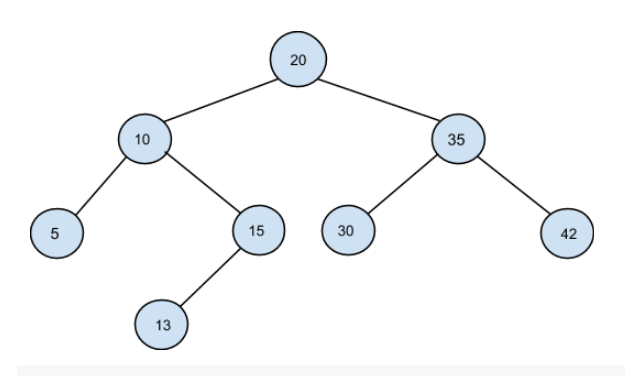
example

Follow Up

Can you do this without using any extra space?

Input Format

The first line contains elements in the level order form. The input consists of values of nodes separated by a single space in a single line. In case a node is null, we take -1 on its place.

Example :

The input for the tree is depicted in the below image:

BT - 2

1 3 8 5 2 7 -1 -1 -1 -1 -1 -1 -1

Explanation :

Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 3
Right child of 1 = 8

Level 3 :
Left child of 3 = 5
Right child of 3 = 2
Left child of 8 =7
Right child of 8 =  null (-1)


Level 4 :
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 2 = null (-1)
Right child of 2 = null (-1)
Left child of 7 = null (-1)
Right child of 7 = null (-1)

1
3 8
5 2 7 -1
-1 -1 -1 -1 -1 -1

Note :

1. The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.

2. The input ends when all nodes at the last level are null(-1).

3. The above format was just to provide clarity on how the input is formed for a given tree. The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 3 8 5 2 7 -1 -1 -1 -1 -1 -1 -1

Output Format:

The output contains the 'N' single space-separated level order traversal of the restored tree.

Note:

You don’t have to print anything, it has already been taken care of. Just implement the function.

Solve now

Approaches

01 Approach

The steps are as follows:

Maintain an array, say ‘INORDERTRAVERSAL’, and store the inorder traversal of the given BST in this array.
Now sort the ‘INORDERTRAVERSAL’ array.
After sorting, we have the valid BST’s inorder traversal.
Again, traverse the tree in inorder fashion and keep updating the value at each node according to the ‘inOrderTraversal’ array.

Algorithm for storing inorder traversal :

void inorder('ROOT', ‘INORDERTRAVERSAL’)

Until all the nodes are traversed
- Recursively traverse the left subtree.
- Add the current node’s value to the ‘INORDERTRAVERSAL’ array.
- Recursively traverse the right subtree.

Solve now

02 Approach

The steps are as follows:

Maintain an array, say ‘INORDERTRAVERSAL’, and store the inorder traversal of the given BST in this array.
Traverse the array from left to right and find these two out-of-order values and swap them.
After swapping, we have the valid BST’s inorder traversal.
Again, traverse the tree in an inorder fashion and keep updating the value at each node according to the ‘INORDERTRAVERSAL’ array.

For example:

Consider, ‘INORDERTRAVERSAL’ = { 10, 50, 30, 40, 20, 60 }.

For a valid BST, this ‘INORDERTRAVERSAL’ should be sorted in ascending order.

We can see that 50 is larger than 30 and it should come after 30. So, 50 is our first incorrect node.

When we found our first incorrect node, we will keep traversing the array and find the first node which is less than 30, because it should come at the place of 50.

We can see, 20 is our second incorrect node.

Now we will swap 50 and 20.

Solve now

03 Approach

The idea is to visit the tree in an in-order fashion and search for two swapped nodes. After finding the incorrect nodes, we will swap their data.

The steps are as follows:

1. We will maintain a ‘PREV’ node to keep track of the previous node of the current node ‘CURR’.

2. We will also maintain ‘FIRST’ and ‘SECOND’ nodes to store the swapped or incorrect nodes.

3. Initialise three nodes, ‘PREV’, ‘FIRST’, and ‘SECOND’ by NULL.

4. We will use a recursive function that takes the root of the BST, ‘PREV’, ‘FIRST’, and ‘SECOND’ as arguments.

5. We will find the incorrect pair by comparing the value of the ‘PREV’ node with the value of the ‘CURR’ node.

Note: For a valid BST, the value of the previous node should always be smaller than the value of the current node in the inorder traversal.

6. When the value of the ‘prev’ node is greater than the value of the ‘CURR’ node, it means that we have found an incorrect node. Here, we have two cases :

If it is the first time we found an incorrect pair, the ‘PREV’ node must be the ‘FIRST’ incorrect node.
If it is not the first time we found an incorrect pair, the ‘CURR’ node must be the ‘SECOND’ incorrect node.

7. We will store these nodes and swap the value of these incorrect nodes to recover the BST.

Solve now

04 Approach

The idea is to visit the tree in an inorder fashion and search for two swapped nodes. After finding the incorrect nodes, we will swap their data.

This approach is very similar to the previous approach but here we will not use recursion or any extra data structure to store the nodes. We will be using Morris Traversal.

In inorder traversal, first, we visit the left subtree, then the root node, and the right subtree. As we are not using recursion or stack, we will be creating a back-link between a node and its inorder successor.

Morris traversal is similar to recursive/iterative traversal, but we need to modify the tree structure during the traversal. Before visiting the left tree of a root, we will build a back-link between the rightmost node in the left tree and the root. So, we can go back to the root node when we are done with the left tree. Then we locate the rightmost node in the left subtree again, cut the back-link, recover the tree structure and start visiting the right subtree.

For example: In the picture below, back-links between (4-2) and (5-1) are created.

When we are done visiting 4, we can go to the next node of 4 in its inorder traversal (in order successor) using this back-link.
When we are done visiting 5, we can go to the next node of 5 in its inorder traversal (in order successor) using this back-link.

Note: For a valid BST, the value of the previous node should always be smaller than the value of the current node in the inorder traversal.

The steps are as follows:

1. Initialise a current node ‘CURR’ by the root node.

2. Maintain a ‘PREV’ node to keep track of the previous node of the current node ‘CURR’.

3. We will also maintain ‘FIRST’ and ‘SECOND’ nodes to store the incorrect nodes.

4. Initialise ‘PREV’, ‘FIRST’, and ‘SECOND’ by NULL.

5. While ‘CURR’ is not NULL:

We check if ‘CURR’ has a left child.
- If it does not have a left child, we check if the ‘PREV’ node and the ‘CURR’ node form an incorrect pair. When the value of the ‘PREV’ node is greater than the value of the ‘CURR’ node, they form an incorrect pair. Here, we have two cases :
If it is the first time we found an incorrect pair, the ‘PREV’ node must be the ‘FIRST’ incorrect node.
If it is not the first time we found an incorrect pair, the ‘CURR’ node must be the ‘SECOND’ incorrect node. If it has a left child, we first create the back-link from the rightmost node in the left subtree and ‘CURR’. Then, we check if ‘CURR’ and ‘PREV’ form an incorrect pair. When the value of the ‘PREV’ node is greater than the value of the ‘CURR’ node, they form an incorrect pair. Here, we have two cases :
- If it is the first time we found an incorrect pair, the ‘PREV’ node must be the ‘FIRST’ incorrect node.
- If it is not the first time we found an incorrect pair, the ‘CURR’ node must be the ‘SECOND’ incorrect node.
Keep updating the ‘prev’ and the ‘CURR’ node.

6. Now, we will swap the value of these ‘FIRST’ and the ‘SECOND’ nodes to recover the BST.

Solve now