Last Updated: 23 Jul, 2021

Floyd Warshall

Moderate

Asked in companies

Solve now

Problem statement

You have been given a directed weighted graph of ‘N’ vertices labeled from 1 to 'N' and ‘M’ edges. Each edge connecting two nodes 'u' and 'v' has a weight 'w' denoting the distance between them.

Your task is to find the length of the shortest path between the ‘src’ and ‘dest’ vertex given to you in the graph using Flloyd warshall’s algorithm. The graph may contain negatively weighted edges.

Example :

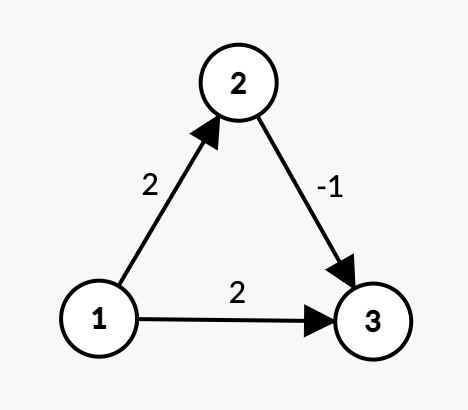
Alt text

3 3 1 3
1 2 2
1 3 2
2 3 -1
In the above graph, the length of the shortest path between vertex 1 and vertex 3 is 1->2->3 with a cost of 2 - 1 = 1.

Note :

It's guaranteed that the graph doesn't contain self-loops and multiple edges. Also the graph does not contain negative weight cycles.

Input Format :

The first line of input contains an integer ‘T’ denoting the number of test cases. Then each test case follows.

The first line of each test case contains four single space-separated integers ‘N’,  ‘M’ , ‘src’ and ‘dest’ denoting the number of vertices, the number of edges in the directed graph the source vertex and the destination vertex respectively.

The next ‘M’ lines each contain three single space-separated integers ‘u’, ‘v’, and ‘w’, denoting an edge from vertex ‘u’ to vertex ‘v’, having weight ‘w’.

Output Format:

For each test case, return an integer denoting the length of the shortest path from ‘src’ to ‘dest’. If no path is possible return 10^9.

Note:

You do not need to print anything, it has already been taken care of. Just implement the given function.

Constraints :

1 <= T <= 10
1 <= N <= 50
1 <= M <= 300
1 <= src, dest <= N
1 <= u,v <= N
-10^5 <= w <= 10^5

Time Limit: 1 sec

Solve now

Approaches

01 Approach

We will create a 2D array ‘D[][]’, where ‘D[i][j]’ stores the shortest distance from vertex ‘i’ to vertex ‘j’.
Initialize the 2D array with an infinite value.
Iterate on the vertices 1 to ‘N’, initialize ‘D[i][i]’ with 0.
Iterate on the edges of the graph, and each edge (‘u’,’v’,’w’) update ‘D[u][v]’, i.e., ‘D[u][v]’ = ‘w’.
Now we will use Dynamic Programming to find the minimum distance between every pair of vertices.
- For(k: 1 to ‘N’){
- For(i: 1 to ‘N’){
- For(j: 1 to ‘N’){
- ‘D[i][j]’ = min(‘D[i][j]’, ‘D[i][k]’ + ‘D[k][j]’)
- }
- }
- }

Solve now