Last Updated: 19 Feb, 2021
k-th node from the end of the linked list
Easy
Asked in companies



Given the head node of the singly linked list and an integer ‘k’, , find the value at the kth node from the end of the linked list.
For example:
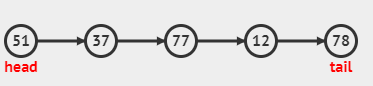
For the above-linked list, if k=2, then the value at the kth i.e second node from the end is ‘12’.
Note :
1.You don’t need to take any input. It has already been taken care of. Just implement the given function and return a pointer pointing to the k-th element from the last of the linked list.
2.It is guaranteed that k<=size of the linked list.
Input Format :
The first line of input contains an integer ‘T’ denoting the number of test cases.
The next ‘2*T’ lines represent the ‘T’ test cases.
The first line of each test case contains integers denoting the nodes of the linked list. Each line is guaranteed to have -1 at the end to signify the end of the linked list.The second line of each test case contains an integer ‘k’
Output Format :
For each test case, return a pointer pointing to the node
which is at the k-th position from the last of the linked list.
Constraints :
1 <= T <= 50
0 <= N <= 10^5
-10^9 <= data <= 10^9
1 <=k <=N
node->data ≠ -1.
Where ‘T’ is the total number of test cases, ‘N’ denotes the number of elements in each Linked List, and ‘data‘ is the value of any node of the linked list and ‘k’ is the position of the element from the end to be returned.
Time Limit : 1 sec
Approaches
- We can find the kth node from end very easily if we know the total number of nodes in the list.
- We take a pointer ‘cur’ (initially pointing to head) and a variable ‘cnt’ to count total number of nodes.
- We move the ‘cur’ pointer forward by one step until we reach NULL and increment the count variable by one in each move.
- We will use the following property to find the kth node from the end.
- Kth node from end = (cnt-k+1)th node from the beginning.
- Let us store the value of cnt-k+1 in a variable ‘n’.
- Now traverse the linked list again and return the pointer to the ‘nth’ node.
Algorithm
- In the naive approach, we have to traverse the linked list twice. We can solve the problem in a single traversal with the help of the algorithm stated below.
- We will take two pointers ‘back’ and ‘front’ (Initialize both to head).
- Move the ‘front’ pointer ‘k’ nodes ahead from the ‘back’ pointer.
- Move both the pointers one step forward in parallel until the ‘front’ pointer reaches the end of the list.
- Now, when the front pointer reaches the end, the back pointer will be pointing to the kth node from the end, hence we return the ‘back’ pointer.
Let us understand the above approach for the below-linked list for k=3.
Step 1: Initialize back and front to head.
*back=5 , *front=5.
Step 2: Move front three(k) steps ahead.
*front=6.
Step 3: Move both pointers one by one until ‘front’ reaches the end.
*back=23 ,*front=43
*back=7 , *front=76
*back=6 , *front=89
*back=43 , front=end
Step 4: ‘back’ points to the kth node from last. Therefore answer is 43.

