Last Updated: 31 Oct, 2020
Spiral Matrix
Easy
Asked in companies



You are given a 2-D array 'MATRIX' of dimensions N x M, of integers. You need to return the spiral path of the matrix.
Example Of Spiral Path:
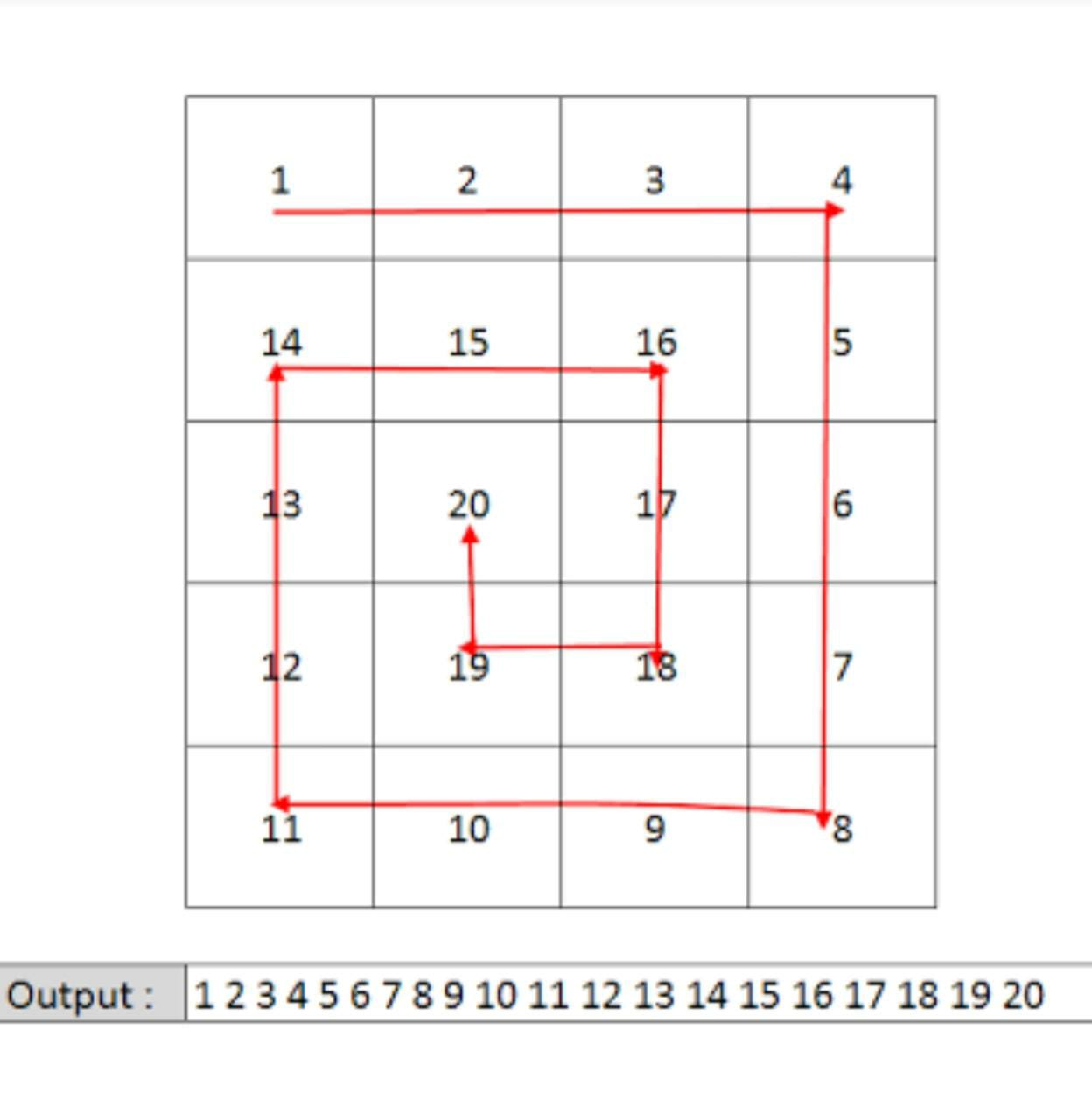
Input Format:
The first line contains an integer 'T' which denotes the number of test cases or queries to be run. Then the test cases follow.
The first line of each test case contains two single space-separated integers 'N' and 'M', denoting the number of rows and columns respectively.
The next 'N' lines, each contains 'M' single space-separated integers representing the elements in a row of the matrix.
Output format :
For each test case/query, print the spiral path of the given matrix.
The output for every test case will be printed in a separate line.
Note:
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 5
1 <= N <= 10 ^ 2
1 <= M <= 10 ^ 2
-10 ^ 9 <= MATRIX[ i ][ j ] <= 10 ^ 9
Time Limit: 1sec.
Approaches
For each boundary, we will use the 4 for loops. Now the problem is reduced to print the remaining submatrix which is handled with the help of recursion. Keep track of new dimensions(rows and columns) of the current submatrix which are passed with the help of parameters in each recursion call.
Algorithm:
spiralPrint(matrix[][], R, C, rows, cols):
- Check for base cases, i.e. if outside the boundary of the matrix then return.
- Print the first row from left to right of the matrix i.e from column ‘C’ to ‘cols’, print the elements of the Rth row.
- Print the last column from top to bottom of the matrix i.e from row ‘R’ to ‘rows’, print the elements of the (cols)th column.
- Print the last row from right to left of the matrix i.e from column ‘cols’ to ‘C’, print the elements of the (rows)th row.
- Print the first column from bottom to top of the matrix i.e from row ‘rows’ to ‘R’, print the elements of the Cth column.
- Call the function recursively with the updated values of boundaries, spiralPrint(matrix, R + 1, C + 1, rows - 1, cols - 1).
The idea is to traverse the matrix using for loops where each loop will be used for a specific direction to print all the elements in the clockwise order layer by layer. Every ‘for’ loop traverses the matrix in a single direction. The first loop traverses the matrix from left to right, the second loop traverses the matrix from top to bottom, the third traverses the matrix from the right to left, and the fourth traverses the matrix from bottom to up. After completing the traversal using 4 loops one time repeat it(4 for loops) again for the remaining submatrix. To traverse using these loops we will initialize 4 variables to keep the boundaries of the submatrix as explained below.
Algorithm:
spiralPrint(matrix[][], rows, cols):
- Initialize two variables ‘R’, ‘C’ with 0 to denote the lowest boundary for row and column of the submatrix remaining. Also, rows and cols denote the maximum boundary for the submatrix remaining.
- While(R < rows and C < cols) :
- Print the first row from left to right of the remaining submatrix i.e from column ‘C’ to ‘cols’, print the elements of the Rth row. Increment ‘R’ by 1.
- Print the last column from top to bottom of the remaining submatrix i.e from row ‘R’ to ‘rows’, print the elements of the (cols)th column. Decrement ‘cols’ by 1.
- Print the last row from right to left of the remaining submatrix i.e from column ‘cols’ to ‘C’, print the elements of the (rows)th row. Decrement ‘rows’ by 1.
- Print the first column from bottom to top of the remaining submatrix i.e from row ‘rows’ to ‘R’, print the elements of the Cth column. Increment ‘C’ by 1.

