Binary Tree Multiplication

Moderate
0/80
profile
Contributed by
2 upvotes
Asked in companies
Paytm (One97 Communications Limited)D.E.ShawGlobal Logic

Problem statement

Ninja has a binary tree. He wants to find the sum of multiplication of each node of the binary tree with its mirror node. Help Ninja to find the sum.

The mirror of a node is a node that is present at the mirror position in the opposite subtree at the root. The mirror of the root node is the node itself.

The answer can be very large, so print answer modulo 1000000007.

For Example :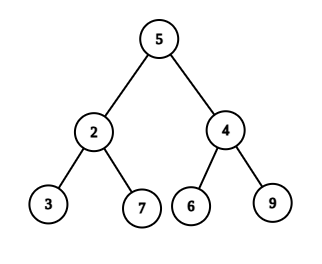 

In this example, The mirror of 2 will be 4, the mirror of 3 will be 9 and the mirror of 7 will be 6 so the final answer is (5 * 5) + (2 * 4) + (3 * 9) + (7 * 6) = 102.
Note : 
Every Node has a mirror node in the given tree.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line contains a single integer ‘T’ denoting the number of test cases. Then each test case follows.

The first line of each test case contains the elements of the binary tree in the level order form separated by a single space.

If any node does not have a left or right child, take -1 in its place. Refer to the example below.


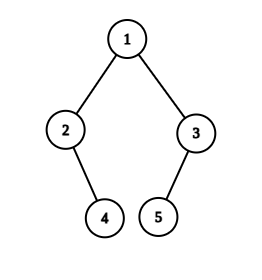
1
2 3
-1 4 5 -1
-1 -1 -1 -1
Explanation :
Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = null (-1)
Right child of 2 = 4
Left child of 3 = 5
Right child of 3 = null (-1)

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = null (-1)
Left child of 5 = null (-1)
Right child of 5 = null (-1)

The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.

The input ends when all nodes at the last level are null (-1).

Note: The above format was just to provide clarity on how the input is formed for a given tree. 

The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 2 3 -1 4 5 -1 -1 -1 -1 -1
Output Format : 
For each test case, print a single integer denoting the sum of multiplication of each node with its mirror node.

Output for each test case will be printed in a separate line.
Note : 
You are not required to print anything; it has already been taken care of. Just implement the function and return the answer.
Constraints : 
1 <= T <= 100
1 <= N <= 3000
1 <= nodeVal <= 10000

Where ‘nodeVal’ is the value of the node.

Time Limit: 1sec
Sample Input 1 :
2
3 2 1 -1 -1 -1 -1
1 2 3 -1 4 5 -1 -1 -1 -1 -1
Sample Output 1 :
11
27
Explanation For Sample Output 1 :

For the First Test Case, the mirror of 3 is 3 itself and the mirror of 2 is 1. So the final answer will be (3 * 3) + (2 * 1) = 11.


For the second Test Case, The mirror of 2 will be 3 and the mirror of 4 will be 5. So the final answer is (1 * 1) + (2 * 3) + (4 * 5) = 27.
Sample Input 2 :
2
5 5 5 -1 -1 -1 -1
1 2 3 4 5 6 7 -1 -1 -1 -1 -1 -1 -1 -1
Sample Output 2 :
50
65
Hint

Traverse through the tree using left and right nodes and multiply the mirror nodes

Approaches (1)
Tree Traversal

Let’s look at what a mirror node of any node will be. So let’s say we are at some node in the left subtree and want to find the mirror of the current node, so it will be present in the right subtree but will have opposite parents than the current node, i.e. for example if the current node is at: root -> left -> left -> right then its mirror will be at root -> right -> right -> left. Hence what we can do is call a function and pass the right node as a mirror node if we have selected a left node and vice versa.


The steps are as follows:

  1. Take an integer ‘answer’ in which we will store the final answer.
  2. Update the value of ‘answer’ as ‘answer’ + (‘root -> data’ * ‘root -> data’) as the mirror of the root node will be the node itself.
  3. Now call the function ‘mirrorMultiplicationHelper’ and pass left subtree, right subtree and ‘answer’.
  4. Return ‘answer’.

 

‘mirrorMultiplicationHelper’(left, right, answer):

  1. Check if the left and right nodes are not empty.
  2. Update the value of ‘answer’ as (‘answer’ + ‘left -> data’ * ‘right -> data’) % 1000000007.
  3. Call the function ‘mirrorMultiplicationHelper’ for the left side of the left subtree and right side of the right subtree.
  4. Call the function ‘mirrorMultiplicationHelper’ for the right side of the left subtree and the left side of the right subtree.
Time Complexity

O(N), where N is the number of nodes.


We will visit all the nodes of the tree.

Hence the time complexity will be O(N).

Space Complexity

O(1).


As we are not using any space.

Hence the space complexity will be O(1).

Code Solution
(100% EXP penalty)
Binary Tree Multiplication
Full screen
Console