Best Time to Buy and Sell Stock III

Hard
0/120
Average time to solve is 10m
profile
Contributed by
14 upvotes
Asked in companies
FacebookAppleOla

Problem statement

Given an array "prices". In "prices" the ith element is the price of the stock on the ith day. Your task is to find maximum profit at the end of the ith day. You may complete at max 2 transactions.

You can perform a transition with these conditions -

1. Not allowed to engage in more than 1 transaction at a time, which means if you have bought stock then you can buy another stock before selling the first stock.

2. If you bought a stock at ‘X’ price and sold it at ‘Y’ price then the profits ‘Y - X’.
Note: 
It is not compulsory to perform an exact '2' transaction.
Detailed explanation ( Input/output format, Notes, Images )
Input format: 
The first line of input contains an integer 'T' denoting the number of test cases.

The first line of each test case contains a single integer 'N', 'N' denotes the length of array ‘prices’.

The second line of each test case contains an 'N' space-separated integers, in which every integer denotes an element of the array "prices".
Output Format 
For each test case, you need to print the maximum profit made by selling the stocks.
Note : 
You do not need to print anything; it has already been taken care of.
Constraints: 
1 <= T <= 50
1 <= N <= 10^4
0 <= A[i] <= 10^9

Time limit: 1 second
Sample Input 1:
2
7
3 3 5 0 0 1 4
6
1 2 3 3 6 9
Sample Output 1:
6
8
Explanation For Sample Input 1:
Test Case 1:

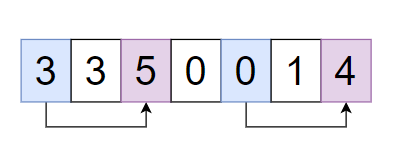
subsequence

Buy the first stock at ‘0-th’ day and sell at ‘2-nd’ day - ‘profit = 5 - 3 = 2’
Buy the second stock at ‘4’th day and sell at ‘6’th day - ‘profit = 4 - 0 = 4’
Total profit ‘2 + 4 = 6’.

Test Case 2:

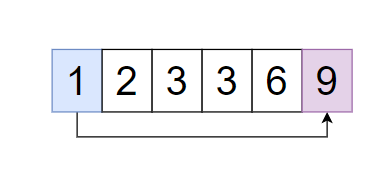
subsequence

Buy the stock at ‘0’ day and sell at ‘5’ day - ‘profit = 9 - 1 = 8’.

Suppose we bought the first stock at ‘0-th ‘ day and sold at ‘2-nd’ then the profit will be ‘3 - 1 = 2’ and second stock at ‘3-rd’ day and sold at ‘5-th’ day then the profit will be ‘9 - 3 = 6’  so total profit ‘2 + 6 = 8’.
But there is no other possibility to get more profit than ‘8’.
Sample Input 2:
2
5   
1 2 4 3 2
4
9 8 7 6
Sample Output 2:
3
0
Hint

Try to find all the possible combinations.

Approaches (2)
Brute Force

The basic idea is that, try all possible transactions, means move to every index and try to perform one transaction before the current index and one after the current index. For all the possibilities choose maximum.

 

  • ‘ans = 0’, to store answers as maximum profit.
  • Iterate a loop ‘i’ from ‘0’ to ‘n - 2’.
  • For every ‘i’, find the best transaction on the left side of right, which means iterate a loop ‘j’ from ‘0’ to ‘i’.
  • ‘best transaction on left side = current value - minimum so far’.
  • For every ‘i’, find the best transaction on the right side of the right, which means iterate a loop ‘j’ from ‘i + 1’ to ‘n - 1’.
  • ‘best transaction on right side = current value - minimum so far’.
  • If ‘(best transaction on left side ) + (best transaction on right side) > ans’,
  • Update ‘ans= (best transaction on left side ) + (best transaction on right side)’.
  • In the end, return ‘ans’.
Time Complexity

O(N ^ 2), Where ‘N’ is the size of the given ‘prices’.

 

We are iterating two nested loops of size ‘N’, hence the complexity is O(N ^ 2).

Space Complexity

O(1)

 

Since we are using constant space.

Code Solution
(100% EXP penalty)
Best Time to Buy and Sell Stock III
Full screen
Console