Problem
Submissions
Hints & solutions
Discuss
Chocolate Problem
Moderate
0/80
Average time to solve is 15m
Problem statement
Given an array/list of integer numbers 'CHOCOLATES' of size 'N', where each value of the array/list represents the number of chocolates in the packet. There are ‘M’ number of students and the task is to distribute the chocolate to their students. Distribute chocolate in such a way that:
1. Each student gets at least one packet of chocolate.
2. The difference between the maximum number of chocolate in a packet and the minimum number of chocolate in a packet given to the students is minimum.
Example :
Given 'N' : 5 (number of packets) and 'M' : 3 (number of students)
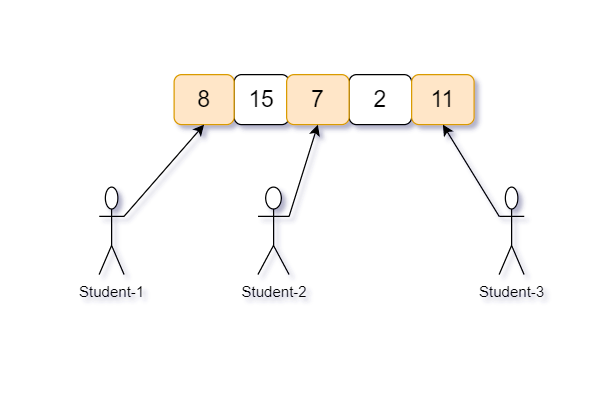
And chocolates in each packet is : {8, 11, 7, 15, 2}
All possible way to distribute 5 packets of chocolates among 3 students are -
( 8,15, 7 ) difference of maximum-minimum is ‘15 - 7’ = ‘8’
( 8, 15, 2 ) difference of maximum-minimum is ‘15 - 2’ = ‘13’
( 8, 15, 11 ) difference of maximum-minimum is ‘15 - 8’ = ‘7’
( 8, 7, 2 ) difference of maximum-minimum is ‘8 - 2’ = ‘6’
( 8, 7, 11 ) difference of maximum-minimum is ‘11 - 7’ = ‘4’
( 8, 2, 11 ) difference of maximum-minimum is ‘11 - 2’ = ‘9’
( 15, 7, 2 ) difference of maximum-minimum is ‘15 - 2’ = 13’
( 15, 7, 11 ) difference of maximum-minimum is ‘15 - 7’ = ‘8’
( 15, 2, 11 ) difference of maximum-minimum is ‘15 - 2’ = ‘13’
( 7, 2, 11 ) difference of maximum-minimum is ‘11 - 2’ = ‘9’
Hence there are 10 possible ways to distribute ‘5’ packets of chocolate among the ‘3’ students and difference of combination (8, 7, 11) is ‘maximum - minimum’ = ‘11 - 7’ = ‘4’ is minimum in all of the above.
Detailed explanation ( Input/output format, Notes, Images )
Input format :
The first line of input contains an integer ‘T’ denoting the number of test cases.
The next ‘2*T’ lines represent the ‘T’ test cases.
The first line of each test case contains two space-separated integers ‘N’ denoting the number of packets of chocolate and ‘M’ denotes the number of students.
The second line of each test case contains ‘N’ space-separated integers denoting the number of chocolate in each of ‘N’ packets.
For each test case, print the minimum difference of the chocolates contained in the packets distributed to the students.
You don't need to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 50
2 <= M <= N <= 10^4
1 <= CHOCOLATES[i] <= 10^9
Time Limit : 1 sec
Sample Input 1 :
2
3 2
7 2 4
4 3
3 5 1 6
Sample Output 1 :
2
3
Explanation For Sample Input 1 :
Test Case 1 :
All possible way to distribute 3 packets of chocolate among 2 students are -
( 7, 2 ) difference is ‘7 - 2’ = ‘5’
( 7, 4 ) difference is ‘7 - 4’ = ‘3’
( 2, 4 ) difference is ‘4 - 2’ = ‘2’
There are three ways to distribute 3 packets of chocolate among 2 students but pair ( 4, 2 ) has minimum difference in ‘maximum - minimum’ = ‘4 - 2’ = ‘2’
Hence answer is ‘2’
Test Case 2 :
All possible way to distribute 4 packets of chocolate among 3 students are -
( 3, 5, 1 ) difference is ‘5 - 1’ = ‘4’
( 5, 1, 6 ) difference is ‘6 - 1’ = ‘5’
( 1, 6, 3 ) difference is ‘6 - 1’ = ‘5’
( 6, 5, 3 ) difference is ‘6 - 3’ = ‘3’
There are four options to choose 3 packets of chocolate. Only ( 6, 5, 3 ) pair has the minimum difference ‘6 - 3’ = ‘3’ comparing other pair of difference ( 4, 5, 5 )
Hence answer is ‘3’
Sample Input 2 :
2
7 3
7 3 2 4 9 12 56
8 5
3 4 1 9 56 7 9 12
Sample Output 2 :
2
6
Hint
Hint 1
Hint 2
Try to generate all possible subsets.
Approaches (2)
Approach 1
Approach 2
Recursion
The idea is that generate all the possible subsets of size ‘M’ and checks the minimum difference that can be possible from all subsets.
- This problem can be solved using recursion and the idea behind this is to generate all the possible minimum differences from the given array.
- To store minimum difference we use a variable (say, ‘minVal’) and the initial value is ‘INFINITE’
- For each element we will have two choices: either to include it in the first subset or not. So, at each stage, we will make two recursive calls, one which will consider including the current element and others which won’t. We will explore the depth taking into consideration each of the two possible cases.
- When we have no elements to explore we will then check our condition on a particular set that can make a minimum difference.
- Suppose we are at set ‘S’ and the size of ‘S’ is ‘M’ then find a ‘minimum’ and ‘maximum’ value of set ‘S’ and compare is 'maximum' - ‘minimum’ is less than ‘minVal’
- If yes then update ‘minVal’ with ‘maximum’ - ‘minimum’
- Finally, return ‘minVal’
Time Complexity
O(2 ^ N), where ‘N’ is the number of integers in the array.
Each number has two choices, whether to include it in a set or not. There are total ‘N’ numbers present with us, so the total possible combinations will be 2 * 2 * 2… (‘N’ times). Hence, the overall time complexity will be O(2 ^ N).
Space Complexity
O(N), where ‘N’ is the number of elements in the array.
This space is used to store the recursion stack. Our algorithm works in a depth - first way, so we cannot have more than ‘N’ recursive calls on the stack as the total numbers present can be at max ‘N’. Hence, the overall space complexity will be O(N).
Code Solution
(100% EXP penalty)
Chocolate Problem
Javascript (node v10.20.0)
Console



