Problem

Submissions

Hints & solutions

Discuss

Count Strongly Connected Components (Kosaraju’s Algorithm)

Hard

0/120

Average time to solve is 40m

Contributed by

71 upvotes

Asked in companies

Problem statement

You are given an unweighted directed graph having 'V' vertices and 'E' edges. Your task is to count the number of strongly connected components (SCCs) present in the graph.

A directed graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of a graph are the subgraphs which are themselves strongly connected.

Note :

Use zero-based indexing for the vertices.

The given graph doesn’t contain any self-loops.

Detailed explanation ( Input/output format, Notes, Images )

Input Format :

The very first line of input contains an integer ‘T’ denoting the number of test cases.

The first line of every test case contains two space-separated integers ‘V’ and ‘E’ denoting the number of vertices and the number of edges present in the graph. 

The next ‘E’ lines contain two space-separated integers ‘a’ and ‘b’ denoting a directed edge from vertex ‘a’ to ‘b’.

Output Format :

For each test case, return an integer denoting the number of strongly connected components (SCCs) present in the graph.

Note :

You do not need to print anything, it has already been taken care of. Just implement the given function.

Constraints :

1 <= T <= 10
1 <= V <= 10^4
0 <= E <= 10^4
0 <= a, b < V

Time Limit: 1 sec

Sample Input 1 :

Sample Output 1 :

Explanation of sample input 1 :

For the first test case, the graph is shown below. There are two SCCs in the graph, which are enclosed in the boxes as shown in the image below.

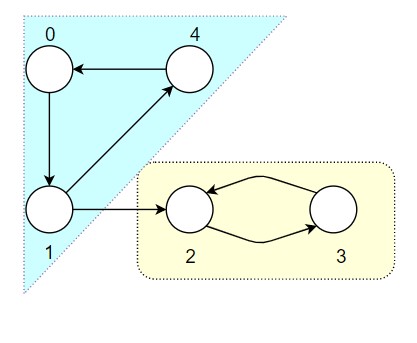
Sample Input 2 :

Sample Output 2 :

1
2

Hint 1

Can you solve the problem using Kosaraju’s Algorithm?

Approaches (1)

Approach 1

Using Kosaraju's Algorithm

Kosaraju’s algorithm can find the strongly connected components (SCCs) of a graph in linear time.

The idea behind this algorithm is to use the finish time of the vertices to generate the SCCs.
The finish time of a vertex is the time at which the exploration of the vertex completes.
Let’s assume that the finish time for an SCC is the maximum of the finish time of all the vertices present in that SCC. Then the finish time of an SCC which is connected to any other SCC will always be greater than the finish time of the other SCC. (You can refer here for the proof).
In order to determine the finish times of the vertices, we traverse the graph once. During the traversal, if the exploration of a vertex completes, we push the vertex in a stack.
This gives us the nodes in descending order of their finish times, as the node with a larger finish time will be present closer to the top of the stack.
For example, consider the graph below. After traversing the graph once, we have the nodes stored in the stack in descending order of their finish time. The starting and the finish time for the vertices are shown above each vertex as <start time, finish time>.

The topmost vertex of the stack will belong to the SCC which has the largest finish time and this SCC will be the ‘root’ node of the condensation graph (A condensation graph of a directed graph G is a directed graph G', whose vertices are strongly connected components of G, and the edge in G' is present only if there exists at least one edge between the vertices of corresponding connected components).

Now we want to visit all the SCCs one by one. If we travers the graph starting from the top node of the stack, we will visit all the vertices of the graph and won’t be able to distinguish different SCCs. So, we compute the transpose of the graph by reversing the direction of every edge.
This way the SCCs of the graph remain the same but their order gets reversed i.e. the condensation graph gets reversed.

Now, if we start the traversal from the topmost vertex in the stack, then we only visit the vertices belonging to the same SCC, i.e. SCC 1 here.
We pop the topmost vertex from the stack and repeat the previous step for the remaining unvisited vertices.
In this way, SCC 2 and 3 also are visited and we generate all the SCCs of the graph.

Algorithm:

Create an empty stack to store the vertices in descending order of their finished time.
Create a visited array of size ‘V’ and initialize all the entries to false.
Loop: For ‘i’ in the range 0 to V-1:
- Apply DFS considering ‘i’ as source vertex. While performing DFS we keep track of which vertices have been visited by updating the visited array. As the exploration of vertices present in the DFS tree of ‘i’ is completed, we push them into the stack
Get the transpose of the given graph by reversing the direction of every edge.
Mark all the vertices as unvisited.
Create a variable count to store the count of the SCCs.
Repeat the following steps until the stack becomes empty:
- Pop the top vertex from the stack and store it in a variable say, ‘V’.
- If the vertex ‘V’ is not visited before:
  - Apply DFS, taking ‘V’ as the source vertex. While performing DFS keep track of which vertices have been visited by updating the visited array.
  - Increment ‘COUNT’ by one.
Return ‘COUNT’.

Note:

In the above approach, we have used DFS. You can also use BFS, but the idea will remain the same.

Time Complexity

O(V + E), where ‘V’ and ‘E’ denote the number of vertices and edges in the graph, respectively.

We are traversing the complete graph twice where each traversal takes O(V + E) time. Finding the transpose of the graph takes O(V + E) time. Also, initialising the visited array takes O(V) time. Hence, the overall complexity is 2*O(V + E) + O(V + E) + O(V) = O(V + E).

Space Complexity

O(V + E), where ‘V’ and ‘E’ denote the number of vertices and edges in the graph, respectively.

Extra space is required for the recursion stack. The maximum depth of the stack can be O(V). O(V) extra space is required for maintaining the stack and a visited array. Also, O(V+E) extra space is required for storing the adjacency list of the transpose graph. Hence, the overall space complexity is O(V) + O(V) + O(V) + O(V + E) = O(V + E).

(100% EXP penalty)

Count Strongly Connected Components (Kosaraju’s Algorithm)

Raj Ghosh

Interview problems

JAVA SOLUTION || (Kosaraju’s Algorithm) ||

import java.util.*;

public class Solution {

static Stack<Integer> stack;

static boolean[] visited;

public static int stronglyConnectedComponents(int v, ArrayList<ArrayList<Integer>> edges) {

ArrayList<ArrayList<Integer>> adjList = new ArrayList<>();

for (int i = 0; i < v; i++) {

adjList.add(new ArrayList<>());

}

for (ArrayList<Integer> edge : edges) {

int from = edge.get(0);

int to = edge.get(1);

adjList.get(from).add(to);

}

stack = new Stack<>();

visited = new boolean[v];

for (int i = 0; i < v; i++) {

if (!visited[i]) {

topologicalDFS(i, adjList);

}

ArrayList<ArrayList<Integer>> reversedGraph = reverseArrayGraph(adjList);

visited = new boolean[v];

int count = 0;

while (!stack.isEmpty()) {

int node = stack.pop();

if (!visited[node]) {

count++;

dfs(node, reversedGraph);

}

return count;

}

public static void topologicalDFS(int idx, ArrayList<ArrayList<Integer>> edges) {

if (visited[idx])

return;

visited[idx] = true;

for (int nbr : edges.get(idx)) {

topologicalDFS(nbr, edges);

}

stack.add(idx);

}

public static ArrayList<ArrayList<Integer>> reverseArrayGraph(ArrayList<ArrayList<Integer>> edges) {

int n = edges.size();

ArrayList<ArrayList<Integer>> reversedEdges = new ArrayList<>(n);

for (int i = 0; i < n; i++) {

reversedEdges.add(new ArrayList<>());

}

for (int u = 0; u < n; u++) {

for (int v : edges.get(u)) {

reversedEdges.get(v).add(u);

}

return reversedEdges;

}

public static void dfs(int idx, ArrayList<ArrayList<Integer>> edges) {

if (visited[idx])

return;

visited[idx] = true;

for (int nbr : edges.get(idx)) {

dfs(nbr, edges);

}

15 views

0 replies

0 upvotes

Abdul Ikram

Interview problems

Easy C++ Solution (Kosaraju's Algorithm) || All Test Case Passed

#include<unordered_map>

#include<list>

#include<stack>

void dfs(int node, vector<int> &visited, unordered_map<int, list<int>> &adj, stack<int> &stk){

visited[node] = true;

for(auto neighbour:adj[node]){

if(!visited[neighbour]){

dfs(neighbour, visited, adj, stk);

}

stk.push(node);

}

void reverseDFS(int node, vector<int> &visited, unordered_map<int, list<int>> &adj){

visited[node] = true;

for(auto neighbour:adj[node]){

if(!visited[neighbour]){

reverseDFS(neighbour, visited, adj);

}

int stronglyConnectedComponents(int v, vector<vector<int>> &edges)

{

unordered_map<int, list<int>> adj;

for(int i=0;i<edges.size();i++){

adj[edges[i][0]].push_back(edges[i][1]);

}

vector<int> visited(v, false);

stack<int> stk;

// Step 01 -> Topological Sort:

for(int i=0;i<v;i++){

if(!visited[i]){

dfs(i, visited, adj, stk);

}

// Step 02 -> Transpose:

unordered_map<int, list<int>> transpose;

for(int i=0;i<v;i++){

visited[i] = false;

for(auto neighbour:adj[i]){

transpose[neighbour].push_back(i);

}

// Step 03 -> Do DFS call using above ordering:

int count = 0;

while(!stk.empty()){

int top = stk.top();

stk.pop();

if(!visited[top]){

count++;

reverseDFS(top, visited, transpose);

}

return count;

}

154 views

0 replies

0 upvotes

Abhishek Sachdeva

Interview problems

easy c++ code || upvote || count strongly connected components

#include <bits/stdc++.h>

void topologicalsort(vector<vector<int>>&adj,vector<bool>&vistied,stack<int>&s,int node)

{

vistied[node]=true;

for(auto child:adj[node])

{

if(!vistied[child])

{

topologicalsort(adj,vistied,s,child);

}

s.push(node);

}

void dfs(vector<vector<int>>&adj,vector<bool>&vistied,int node)

{

vistied[node]=true;

for(auto child:adj[node])

{

if(!vistied[child])

{

dfs(adj,vistied,child);

}

int stronglyConnectedComponents(int v, vector<vector<int>> &edges)

{

// Write your code here.

vector<vector<int>>adj(v);

for(int i=0; i<edges.size(); ++i)

{

int x = edges[i][0];

int y = edges[i][1];

adj[x].push_back(y);

}

//toplogical sort

stack<int>s;

vector<bool>vistied(v,false);

for(int i=0; i<v; ++i)

{

if(!vistied[i])

{

topologicalsort(adj,vistied,s,i);

}

//inverse the paths

vector<vector<int>>inversedadj(v);

for(int i=0; i<v; ++i)

{

vistied[i]=false;

for(auto child:adj[i])

{

inversedadj[child].push_back(i);

}

//perform dfs on this toplogical sort with inversed adj

int count = 0;

while(!s.empty())

{

int top = s.top();

s.pop();

if(!vistied[top])

{

count++;

dfs(inversedadj,vistied,top);

}

return count;

}

47 views

0 replies

1 upvote

VISHAL SINGH

Interview problems

Python Code

def dfs_helper(n, adj_list, visited, topo_stack):
    visited[n] = True
    for nbr in adj_list[n]:
        if not visited[nbr]:
            dfs_helper(nbr, adj_list, visited, topo_stack)
    topo_stack.append(n)

def get_topo_order(V, edges):
    adj_list = [[] for _ in range(V)]
    for u, v in edges:
        adj_list[u].append(v)

    visited = [False] * V
    topo_stack = []

    for n in range(V):
        if not visited[n]:
            dfs_helper(n, adj_list, visited, topo_stack)

    return topo_stack[::-1]

def dfs_helper_scc(n, adj_list, visited):
    visited[n] = True
    for nbr in adj_list[n]:
        if not visited[nbr]:
            dfs_helper_scc(nbr, adj_list, visited)

def stronglyConnectedComponents(V, edges):
    adj_list = [[] for _ in range(V)]
    for u, v in edges:
        adj_list[u].append(v)

    rev_topo_order = get_topo_order(V, edges)
    adj_list_rev = [[] for _ in range(V)]
    for u, v in edges:
        adj_list_rev[v].append(u)

    visited = [False] * V
    scc = 0
    for n in rev_topo_order:
        if not visited[n]:
            scc += 1
            dfs_helper_scc(n, adj_list_rev, visited)

    return scc

python

21 views

0 replies

0 upvotes

Vaibhav Ransing

Interview problems

Java | Kosaraju

import java.util.*;

public class Solution {
	static Stack<Integer> stack;
    static boolean[] visited;

    public static int stronglyConnectedComponents(int v, ArrayList<ArrayList<Integer>> edges) {
        // Step 1: Build the adjacency list from the list of edges
        ArrayList<ArrayList<Integer>> adjList = new ArrayList<>();
        for (int i = 0; i < v; i++) {
            adjList.add(new ArrayList<>());
        }
        for (ArrayList<Integer> edge : edges) {
            int from = edge.get(0);
            int to = edge.get(1);
            adjList.get(from).add(to);
        }

        // Step 2: Perform topological sort and fill the stack
        stack = new Stack<>();
        visited = new boolean[v];
        for (int i = 0; i < v; i++) {
            if (!visited[i]) {
                topologicalDFS(i, adjList);
            }
        }

        // Step 3: Reverse the graph
        ArrayList<ArrayList<Integer>> reversedGraph = reverseArrayGraph(adjList);

        // Step 4: Process all vertices in the order defined by the stack
        visited = new boolean[v];
        int count = 0;
        while (!stack.isEmpty()) {
            int node = stack.pop();
            if (!visited[node]) {
                count++;
                dfs(node, reversedGraph);
            }
        }

        return count;
    }

    // step 1 fill the stack and get topological sort
    public static void topologicalDFS(int idx, ArrayList<ArrayList<Integer>> edges) {
        if (visited[idx])
            return;
        visited[idx] = true;

        for (int nbr : edges.get(idx)) {
            topologicalDFS(nbr, edges);
        }
        stack.add(idx);
    }

    // step 2 reverse the graph
    public static ArrayList<ArrayList<Integer>> reverseArrayGraph(ArrayList<ArrayList<Integer>> edges) {
        int n = edges.size();
        ArrayList<ArrayList<Integer>> reversedEdges = new ArrayList<>(n);

        // Initialize the reversed adjacency list
        for (int i = 0; i < n; i++) {
            reversedEdges.add(new ArrayList<>());
        }

        // Iterate over each vertex and its adjacency list
        for (int u = 0; u < n; u++) {
            for (int v : edges.get(u)) {
                // Add an edge from v to u in the reversed graph
                reversedEdges.get(v).add(u);
            }
        }

        return reversedEdges;
    }

    // step 3
    public static void dfs(int idx, ArrayList<ArrayList<Integer>> edges) {
        if (visited[idx])
            return;
        visited[idx] = true;

        for (int nbr : edges.get(idx)) {
            dfs(nbr, edges);
        }
    }
}

java

33 views

0 replies

0 upvotes

Vikesh Kumar

Interview problems

C++ || Kosaraju's Algo || Using SCC || Easy Soution

Step 1: Adj list

Step 2: Topological Sort

Step 3: Transpose graph

Step 4: DFS call

#include <unordered_map>
#include <list>
#include <stack>

void dfs(int node,unordered_map<int,bool>&vis,stack<int>&s,unordered_map<int, list<int> >&adj){
	vis[node]= true;
	for(auto neighbour : adj[node]){
		if(!vis[neighbour]){
			dfs(neighbour,vis,s,adj);

		}
	}
	s.push(node);
}
void redfs(int node,unordered_map<int,bool>&vis, unordered_map<int, list<int> >&transpose){
	vis[node]= true;
	for(auto neighbour : transpose[node]){
		if(!vis[neighbour]){
			redfs(neighbour,vis,transpose);

		}
	}
}
int stronglyConnectedComponents(int v, vector<vector<int>> &edges)
{
	// Write your code here.

	// STEP 1: adj list
	unordered_map<int, list<int> >adj;
	for(int i=0; i<edges.size(); i++){
		int u =edges[i][0];
		int v= edges[i][1];

		adj[u].push_back(v);
	}

	// STEP 2:topoligical sort
	stack<int>s;
	unordered_map<int,bool>vis;
	for(int i=0; i<v; i++){
		if(!vis[i]){
			dfs(i,vis,s,adj);
		}
	}

	//STEP 3: transpose graph
    unordered_map<int, list<int> >transpose;
	// method 1
	/*for(int i=0; i<v; i++){
		vis[i]= false;
		for(auto nbr:adj[i]){
			transpose[nbr].push_back(i);
		}
	}*/

	// method 2
	for(int i=0; i<edges.size(); i++){
		int u =edges[i][0];
		int v= edges[i][1];

		transpose[v].push_back(u);
	}
	for(int i=0; i<v; i++){
		vis[i] =false;
	}
    
	//STEP 4:dfs call using above ordering
	int cnt =0;
	while(!s.empty()){
		int top =s.top();
		s.pop();
		if(!vis[top]){
			cnt++;
			redfs(top,vis,transpose);
		}
	}
	return cnt;

}

137 views

0 replies

2 upvotes

Samaxyyyy

Interview problems

code error

#include<unordered_map>

#include<stack>

#include<list>

void dfs(int node ,unordered_map<int,bool>&visited,unordered_map<int,list<int> >adj,stack<int>&st ){

visited[node]=true;

for(auto nbr: adj[node]){

if(!visited[nbr]){

dfs(nbr,visited,adj,st);

}

// topological sort condition

st.push(node);

}

void revdfs(int node ,unordered_map<int,bool>&visited,unordered_map<int,list<int> >&transpose ){

visited[node]=true;

for(auto nbr : transpose[node]){

if(!visited[nbr]){

revdfs(nbr,visited,transpose);

}

int stronglyConnectedComponents(int v, vector<vector<int>> &edges)

{

// create adj list

unordered_map<int,list<int> >adj;

for(int i=0; i<edges.size(); i++){

int u = edges[i][0];

int v= edges[i][1];

adj[u].push_back(v);

}

// topo sort

unordered_map<int,bool>visited;

stack<int>st;

for(int i=0; i<v; i++){

if(!visited[i]){

dfs(i,visited,adj,st);

}

// create a transpose graph

unordered_map<int,list<int>>transpose;

for (int i = 0; i < v; i++) {

visited[i]=0;

for (auto nbr : adj[i]){

transpose[nbr].push_back(i);

}

// last step

int count = 0;

while(!st.empty()){

int top = st.top();

st.pop();

if(!visited[top]){

count++;

revdfs(top,visited,transpose);

}

return count;

}

what is the problem that it runs only for 10/11 cases

44 views

0 replies

0 upvotes

Interview problems

Count Strongly Connected Components (Kosaraju’s Algorithm) .C++ Solution . Easy Solution . TC=O(V+E)

#include<bits/stdc++.h>

void DFSFill(int u,unordered_map<int,vector<int>>&adj,vector<bool>&visited,stack<int>&st){

visited[u]=true;

for(int &v:adj[u]){

if(!visited[v]){

DFSFill(v,adj,visited,st);

}

st.push(u);

}

void DFSTraversal(int u,vector<vector<int>>&adjReversed,vector<bool>&visited){

visited[u]=true;

for(int &v:adjReversed[u]){

if(!visited[v]){

DFSTraversal(v,adjReversed,visited);

}

int stronglyConnectedComponents(int V, vector<vector<int>> &edges)

{

// Write your code here.

unordered_map<int,vector<int>>adj;

for(vector<int>vec:edges){

int u=vec[0];

int v=vec[1];

adj[u].push_back(v);

}

stack<int>st;

vector<bool>visited(V,false);

for(int i=0;i<V;i++){

if(!visited[i]){

DFSFill(i,adj,visited,st);

}

vector<vector<int>>adjReversed(V);

for(int u=0;u<V;u++){

for(int &v:adj[u]){

adjReversed[v].push_back(u);

}

int countScc=0;

visited=vector<bool>(V,false);

while(!st.empty()){

int node=st.top();

st.pop();

if(!visited[node]){

DFSTraversal(node,adjReversed,visited);

countScc++;

}

return countScc;

}

178 views

0 replies

0 upvotes

Harsh Jaiswal

Interview problems

easy c++ solution of kosaraju's algorithm

#include<unordered_map>

#include<list>

#include<stack>

#include<limits>

void dfs(int node, stack<int>&st, unordered_map<int, bool>&vis, unordered_map<int, list<int>>&adj)

{

vis[node]=true;

for(auto nbr:adj[node])

{

if(!vis[nbr])

{

dfs(nbr, st, vis, adj);

}

//toppo logic

st.push(node);

}

void revDfs(int node,unordered_map<int, bool>&vis,unordered_map<int, list<int>>&transpose)

{

vis[node]=true;

for(auto nbr: transpose[node])

{

if(!vis[nbr])

{

revDfs(nbr, vis,transpose);

}

int stronglyConnectedComponents(int v, vector<vector<int>> &edges)

{

// Write your code here.

//adj list

unordered_map<int, list<int>>adj;

for(int i=0;i<edges.size();i++)

{

int u = edges[i][0];

int v = edges[i][1];

adj[u].push_back(v);

}

//toppo sort

stack<int>st;

unordered_map<int, bool>vis;

for(int i=0;i<v;i++)

{

if(!vis[i])

{

dfs(i, st, vis, adj);

}

//create transpose graph

unordered_map<int, list<int>>transpose;

for(int i=0;i<v;i++)

{

vis[i]=0;

for(auto nbr:adj[i])

{

transpose[nbr].push_back(i);

}

//dfs call using above ordering

int count=0;

while(!st.empty())

{

int top=st.top();

st.pop();

if(!vis[top])

{

count++;

revDfs(top, vis, transpose);

}

//returning answer

return count;

}

115 views

0 replies

2 upvotes

RAJESH KUMAR YADAV

Interview problems

C++ || Easy To Understand

#include<unordered_map>

#include<stack>

#include<limits>

#include<list>

void dfs(int node, stack<int>&st, unordered_map<int, bool>&vis, unordered_map<int, list<int>>&adj)

{

vis[node]=true;

for(auto nbr:adj[node])

{

if(!vis[nbr])

{

dfs(nbr, st, vis, adj);

}

//toppo logic

st.push(node);

}

void revDfs(int node,unordered_map<int, bool>&vis,unordered_map<int, list<int>>&transpose)

{

vis[node]=true;

for(auto nbr: transpose[node])

{

if(!vis[nbr])

{

revDfs(nbr, vis,transpose);

}

int stronglyConnectedComponents(int v, vector<vector<int>> &edges)

{

// Write your code here.

//adj list

unordered_map<int, list<int>>adj;

for(int i=0;i<edges.size();i++)

{

int u = edges[i][0];

int v = edges[i][1];

adj[u].push_back(v);

}

//toppo sort

stack<int>st;

unordered_map<int, bool>vis;

for(int i=0;i<v;i++)

{

if(!vis[i])

{

dfs(i, st, vis, adj);

}

//create transpose graph

unordered_map<int, list<int>>transpose;

for(int i=0;i<v;i++)

{

vis[i]=0;

for(auto nbr:adj[i])

{

transpose[nbr].push_back(i);

}

//dfs call using above ordering

int count=0;

while(!st.empty())

{

int top=st.top();

st.pop();

if(!vis[top])

{

count++;

revDfs(top, vis, transpose);

}

//returning answer

return count;

}

113 views

0 replies

1 upvote

Console