Deletion In Circular Linked List

Easy

0/40

Average time to solve is 30m

Contributed by

26 upvotes

Asked in companies

Problem statement

You are given a Circular Linked List of integers, and an integer, 'key'.

You have to write a function that finds the given key in the list and deletes it. If no such key is present, then the list remains unchanged.

For Example :

This is a visualization of the Circular Linked List, represented by:
1 2 3 4 5 -1

Note :

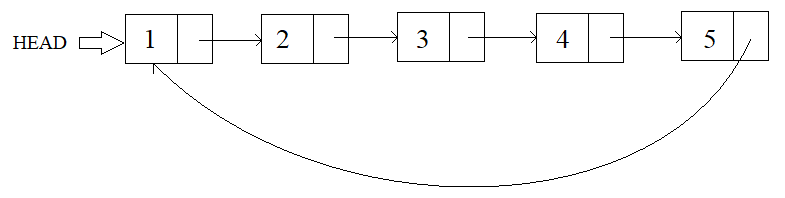
The Circular Linked List before/after deletion may happen to be empty. In that case, only print -1.

All integers in the list are unique.

Detailed explanation ( Input/output format, Notes, Images )

Input format :

The first input line contains the integers present in the circular linked list in order. 

The second input line contains a single integer 'key', the key to be deleted.

Remember/Consider :

-1 marks the end of the linked list however, the tail of the linked list would be pointing to the head making it circular in nature.

Output format :

The only output line contains the updated circular linked list post deletion.

Constraints :

0 <= N <= 10 ^ 5
1 <= key <= 10 ^ 5

Where 'N' is the length of the Circular Linked List.

Time limit: 1 sec

Sample Input 1 :

1 2 3 4 5 -1
3

Sample Output 1 :

1 2 4 5 -1

Explanation for Sample 1 :

The given linked list, before deletion:

After deletion :

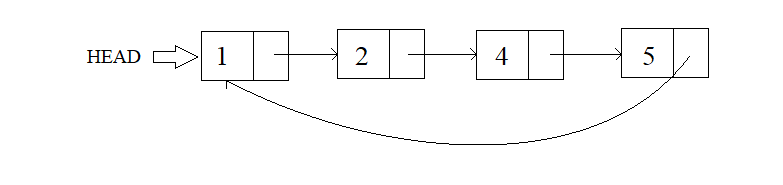
Sample Input 2 :

1 2 3 4 5 -1
1

Sample Output 2 :

2 3 4 5 -1

Console