Duplicate subtree

Moderate
0/80
Average time to solve is 25m
profile
Contributed by
4 upvotes
Asked in companies
AmazonGoogle

Problem statement

You are given a binary tree. You have to find all the duplicate sub-trees of the binary tree. For every duplicate subtree, you just have to return the root of the sub-tree. Two sub-trees are duplicates or the same if the nodes have the same value and the same structure.

Example:- 
For the given binary tree: [1, 2, 1, -1, -1, 2, 1, -1, -1, -1, -1]
Start Node: 3

    1
   / \
 2   1
      / \
     2  1

The answer should be [[2]] because the subtree [2] is present 2 times.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line contains a single integer ‘T’ representing the number of test cases. Then each test case follows.

The first line of each test case contains elements of the tree in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.

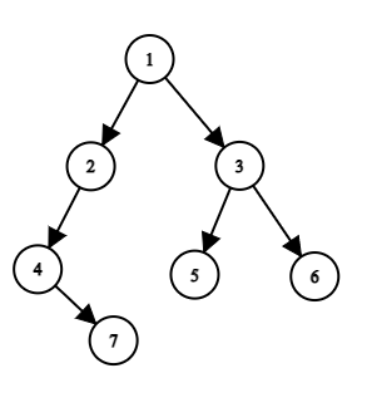
For example, the input for the tree depicted in the above image would be :

1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1
Explanation : 
Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)
Note: 
The above format was just to provide clarity on how the input is formed for a given tree. 
The sequence will be put together in a single line separated by a single space. 
Hence, for the above-depicted tree, the input will be given as:
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Output Format : 
For each test case, print the subtrees that are present more than once in the tree.

The output of each test case should be printed in a separate line.
Note : 
You are not required to print anything, it has already been taken care of. Just implement the function.
Constraints : 
1 <= T <= 5
1 <= N (Number of Nodes) <= 10^5
1 <= VALUE of the nodes <= 10^9

Time Limit = 1 sec
Sample Input 1 :
2
1 2 3 4 -1 -1 5 -1 -1 -1 -1
1 1 1 -1 -1 -1 -1
Sample Output 1 :
1
Explanation for Sample Output 1 :
In the first test case, the tree looks like this:- 


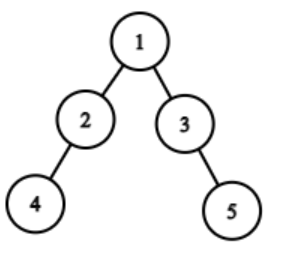
So, there is no duplicate subtree in the tree given above.

In the second test case, the tree looks like this:- 


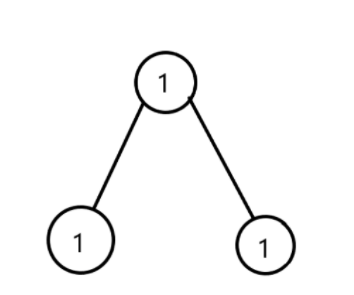
So, the duplicate subtree given is [1].
Sample Input 2 :
1
2 2 2 3 -1 3 -1 -1 -1 -1 -1
Sample Output 2 :
3
2 3
Hint

Use recursion to find whether the subtree is duplicate or not.

Approaches (1)
Recursion

Run backtracking and find the subtrees that are duplicates. Store the current node value and its left and right nodes in a specific order and check whether they are duplicates or not.

 

Algorithm:-

  • Initialize an empty set RESULT to store the nodes that are duplicated.
  • Initialize an empty map named COUNT to store the count of times a specific subtree occurs in the tree.
  • Define a function named FIND with the current node named NODE as a parameter.
    • Recursively call the method FIND with its left and right child.
    • Make a tuple named TUP with the current node’s value and the data returned by its left and right child.
    • If such a tuple already exists, increment COUNT[TUP] by 1.
    • If COUNT[TUP] is greater than equal to 2, add NODE to the RESULT.
    • Return TUP.
  • Return RESULT after converting it into a list.
Time Complexity

O(N ^ 2), where N is the number of nodes.

We are iterating through ‘N’ nodes once and for every node we are checking the data of the node and its left and right subtrees, so the time complexity is O(N ^ 2).

Space Complexity

O(N ^ 2), where N is the number of nodes,

We are iterating through ‘N’ nodes once and for every node we are storing the data of the node and its left and right subtrees, so the space complexity is O(N ^ 2).

Code Solution
(100% EXP penalty)
Duplicate subtree
Full screen
Console