Problem
Submissions
Hints & solutions
Discuss
Euler Path
Hard
0/120
Average time to solve is 15m
Problem statement
You are given an undirected graph 'EDGE_LIST' of ‘N’ nodes and ‘M’ edges. Your task is to return any Euler path of the graph. If no Euler path exists then you need to return -1.
Note :An Euler path is a path in a graph such that every edge must be visited exactly once. You can visit the same vertex multiple times.
Detailed explanation ( Input/output format, Notes, Images )
Input Format
The first line of input contains an integer 'T' representing the number of test cases.
The first line of each test case contains two space-separated integers ‘N’ and ‘M’ where ‘N’ denotes the total number of nodes and ‘M’ denotes the total number of edges in the graph.
The next ‘M’ lines contain two space-separated integers ‘U’ and ‘V’ where ‘U’ and ‘V’ represent the nodes that share an edge from ‘U’ to ‘V’.
For each test case, the output will be 1 if you have returned the correct Euler path, else it will be 0.
The output of each test case will be printed in a separate line.
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 5
1 <= N <= 100
1 <= M <= min(100, N*(N-1)/2)
0 <= U, V <= N - 1
Time Limit: 1 sec
Sample Input 1:
2
3 2
0 1
0 2
4 5
0 1
0 2
0 3
1 2
2 3
Sample Output 1:
1
1
Explanation of Sample Input 1:
Test Case 1 :
The given graph is shown below.
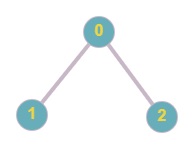
Euler path = 1 -> 0 -> 2
Also, 2 -> 0 -> 1 is also a valid Euler path.
If we return any one of the above two paths then we will get output as 1.
Test Case 2 :
The given graph is shown below.
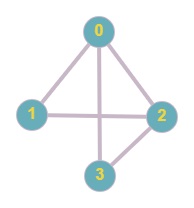
Euler path = 2 -> 0 -> 1 -> 2 -> 3 -> 0
If we return the above path then we will get output as 1.
Note : Here we have visited node 0 and 2 multiple times but we have visited each edge exactly once.
Sample Input 2:
2
5 4
0 4
0 1
1 3
1 2
5 4
0 1
1 2
2 3
3 4
Sample Output 2:
1
1
Explanation of Sample Input 2:
Test Case 1 :
The given graph is shown below.
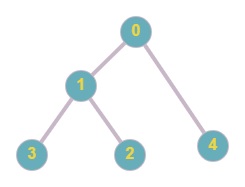
There is no Euler path possible for the above graph. So, we need to return -1.
Test Case 2 :
The given graph is shown below.
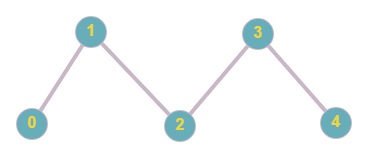
Euler path = 0 -> 1 -> 2 -> 3 -> 4
Hint
Hint 1
Try to find the Euler path starting at 'X' for each vertex 'X'.
Approaches (1)
Approach 1
Fleury's algorithm
The idea here is to use Fleury's algorithm. If the graph contains zero or two nodes having an odd degree then the graph has an Euler Path else not. The idea of Fluery’s algorithm is to first start with an odd degree vertex then at each step visit the edge which is a non – bridge egde.
An edge is said to be a non – bridge if after removal of the edge the graph will still remain connected. We are choosing non – bridge edges here because if we choose the edge which is bridges then we can’t come back to our current node.
Below is the detailed algorithm:
- Declare the following things:
- An array to store the Euler path, say ‘ANSWER’.
- A 2 - D array to store the adjacency list of the graph say, ‘adj’.
- Build an adjacency list using the edges array given in the problem.
- Count the number of nodes with an odd degree, say ‘ODD’.
- If ‘ODD’ is not equal to zero or two then add -1 to ‘ANSWER’ and return ‘ANSWER, as Euler path is not possible in this case.
- If ‘ODD’ == 0, then call the function ‘eulerPath’ with starting node as 0, else find a vertex with odd degree say, 'V' and call function ‘eulerPath’ with starting node as 0 to get ‘ANSWER’.
- Finally, return the ‘ANSWER’.
Description of Euler path function.
This function is used to store the Euler path in ‘ANSWER’.
This function will take 3 arguments
- A variable ‘NODE’ to keep track of the current node.
- A 2 – D ‘ADJ’ which denotes the adjacency list of the graph.
- An array ‘ANSWER’ to store the Euler path.
void eulerPath(‘NODE’, ‘ADJ’, ‘ANSWER’) :
- Visit all neighbours of ‘NODE’
- Say the current neighbour of ‘NODE’ is ‘CURRENT’. Check if the edge from ‘NODE’ to ‘CURRENT’ is a non-bridge edge by calling the function ‘isNonBridge’ function.
- If the edge from ‘NODE’ to ‘CURRENT’ is a non bridge edge then add ‘CURRENT’ to the ‘ANSWER’ and remove edge ‘NODE’ to ‘CURRENT’. Removing edge can be done via removing ‘NODE’ from the adjacency list of ‘CURRENT’ and vice – versa.
- Recur the function for node ‘CURRENT’ i.e. call eulerPath(‘CURRENT’, ‘ADJ’, ‘ANSWER’).
Description of isNonBridge function.
This function is used to check whether the given edge is a non - bridge or not.
This function will take 3 arguments:
- A 2 – D ‘ADJ’ denotes the adjacency list of the graph.
- Two variables 'U' and 'V' denoting an edge between them.
bool isNonBridge (‘U’, ‘V’, ‘ADJ’) :
- If 'V' is the only adjacent node of 'U' then return true.
- Call a dfs function to get the count of all reachable nodes from 'U' before removing the edge from 'U' to 'V' say, ‘WITHOUT_REMOVE’.
- Remove the edge from 'U' to 'V'.
- Call a dfs function to get the count of all reachable nodes from 'U' after removing the edge from 'U' to 'V' say, ‘WITH_REMOVE’.
- Add an edge from 'U' to 'V'.
- If ‘WITH_REMOVE’ >= ‘WITHOUT_REMOVE’ then return true.
- Else, return false.
Description of dfs function:
This function is used to count all reachable nodes from a given node.
This function will take 4 arguments
- A 2 – D ‘ADJ’ denotes the adjacency list of the graph.
- A variable 'U' denoting the current node.
- A variable ‘COUNT’ to count all reachable nodes.
- An array ‘VIS’ to keep track of visited elements.
void dfs(‘U’, ‘COUNT’, ‘ADJ’ , ‘VIS’) :
- Mark 'U' visited as true.
- Increment ‘COUNT’ by 1.
- Visit all neighbours of 'U'
- Say the current neighbour of 'U' is ‘CURRENT’. If we have not visited ‘CURRENT’ then recursively call dfs function to visit ‘CURRENT’ and mark ‘CURRENT’ visited as true.
Time Complexity
O(N * M), where ‘N’ is the total number of nodes and ‘M’ is the total number of edges in the graph.
Where building a graph takes O(M) time as we need to add ‘M’ edges to the graph. Also, the fluery’s algorithm takes O(N * M) as our Euler path function takes O(M) time as we need to check O(M) edges in the worst case. Also, to check the validity of each edge, we are using a function isNonBridge that is taking O(N) time by calling the dfs function as we need to visit O(N) nodes in the worst case.
Hence, the overall time complexity will be O(M) + O(N * M) = O(N * M).
Space Complexity
O(N + M), where ‘N’ is the total number of nodes and ‘M’ is the total number of edges in the graph.
We are using an adjacency list that takes O(M) space as we need to insert ‘M’ edges to the list. Our Euler path function takes O(M) stack space in recursive calls as we can have O(M) edges in the recursive stack. Our dfs functions take O(N) stack space in recursive calls as we can have O(N) nodes in the recursive stack. We are using a visited array that takes O(N) space.
Hence, the overall space complexity will be O(M) + O(M) + O(N) + O(N) = O(N + M).
Code Solution
(100% EXP penalty)
Euler Path
C++ (g++ 5.4)
Console



