Find Center of Star Graph

Easy
0/40
profile
Contributed by
6 upvotes
Asked in companies
MicrosoftCIS - Cyber Infrastructure

Problem statement

You have been given an undirected star graph in the form of Adjacency List 'EDGES', consisting of ‘N’ nodes labelled from 1 to ‘N’. A star graph is a graph where there is one centre node and exactly ‘N’ - 1 edges that connect the centre node to every other node.

You are given a matrix ‘EDGES’ storing the information about the edges, where each row, ‘EDGES[i]’ contains two integers ‘U’ and ‘V’, which implies that there is an undirected edge between ‘U’ and ‘V’.

For Example : 
For the given graph:


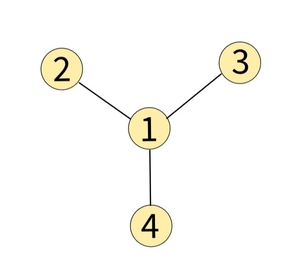
Node 1 is connected to all other nodes. Hence node 1 is the centre of this star graph.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line contains an integer 'T' which denotes the number of test cases.

The first line of each test case contains ‘M’, no of edges.

The following ‘M’ lines contain two integers ‘U’ and ‘V’ denoting there is an undirected edge between node ‘U’ and node ‘V’.
Output Format : 
For each test case, return the centre of the given star graph.

The first and only line of output of each test case prints the centre of a given star graph.
Note : 
You don't need to print anything, it has already been taken care of. Just implement the given function.
Constraints : 
1 ≤ T ≤ 10
3 ≤ M ≤ 10^4
M is always equal to N - 1
EDGES.length = M
1 ≤ U, V ≤ N

Time limit: 1 sec
Sample Input 1 :
2
3
2 1
3 1
1 4
3
1 2
2 3
4 2
Sample Output 1 :
1
2
Explanation of Sample Output 1 :
In test case 1, the graph is shown below.


Node 1 is connected to all other nodes. Hence node 1 is the centre of this star graph.

In test case 2, the graph is shown below.


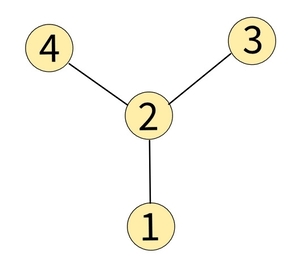
Node 2 is connected to all other nodes. Hence node 2 is the centre of this star graph.
Sample Input 2 :
2
3
2 3
3 1
3 4
4
1 2
2 3
4 2
2 5
Sample Output 2 :
3
2
Explanation of Sample Output 2 :
In test case 1, the graph is shown below.


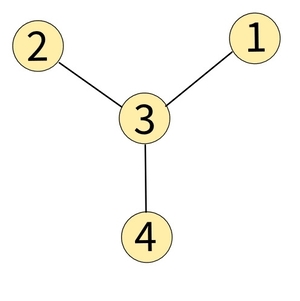
Node 3 is connected to all other nodes. Hence node 3 is the centre of this star graph.

In test case 2, the graph is shown below.


Node 2 is connected to all other nodes. Hence node 2 is the centre of this star graph.
Hint

The centre is the only node that has more than one edge. The centre is also connected to all other nodes.

Approaches (2)
Brute Force

Looking at the problem, we can directly see that the node having ‘M’ number of edges connecting it, where ‘M’ is the number of edges, will be the centre node.

 

The steps are as follows :

  1. Declare a HashMap, ‘mp’ to store the count of edges connecting to a node.
  2. For every edge, we increment the count of its node in ‘mp’.
  3. for ‘e’ in ‘EDGES’:
    • mp[e[0]]++, mp[e[1]]++
  4. Go through ‘mp’ and find the centre of the graph.
  5. for ‘pair’ in ‘mp’:
    • if pair.second == m:
      • return pair.first
Time Complexity

O( N ), where ‘N’ is the total number of nodes in the given graph.

 

We traverse all edges in ~O ( M ) time. At last, we also need to traverse the HashMap, we check for every node in the worst case. But ‘N’ is greater than ‘M’.

Hence the time complexity is O( N ).

Space Complexity

O( N ), where ‘N’ is the total number of nodes in the given graph.

 

We are using a HashMap to store nodes and their connecting edges.

Hence the space complexity is O( N ).

Code Solution
(100% EXP penalty)
Find Center of Star Graph
Full screen
Console