Linear Probing

Easy
0/40
Average time to solve is 15m
37 upvotes
Asked in companies
VisaSpringworksPaxcom

Problem statement

‘Hashing’ is a technique in which a large non-negative integer is mapped with a smaller non-negative integer using a function called ‘hash function’. Hash Table is the table in which we store large numbers corresponding to mapped indices.

While hashing a list of elements, we define ‘Collision’ as a situation when the hash function for a large integer in list returns an index which is already mapped with some other large integer in a list.

‘Linear Probing’ is a collision handling technique in which we find the next vacant place in the hash table for mapping. What we do is that we take the original hash value and successively add 1 in each iteration until an unmapped index is found in the hash table.

Given an array KEYS consisting of N non-negative integers. For each element in a given array, you need to determine the index by which this element is mapped in the hash table if the ‘Linear Probing’ technique is used to handle collision.

The hash function you need to consider is H(X) = X mod N i.e. index = X mod N.

Return an array ‘HASH_TABLE’ of size N in which:

HASH_TABLE[ i ] = KEYS[ j ] where, i = KEYS[ j ] mod N.

In short, an element at index ‘i’ is the element from the given array KEYS which is mapped to that index.

You can refer to the example given below:

alt

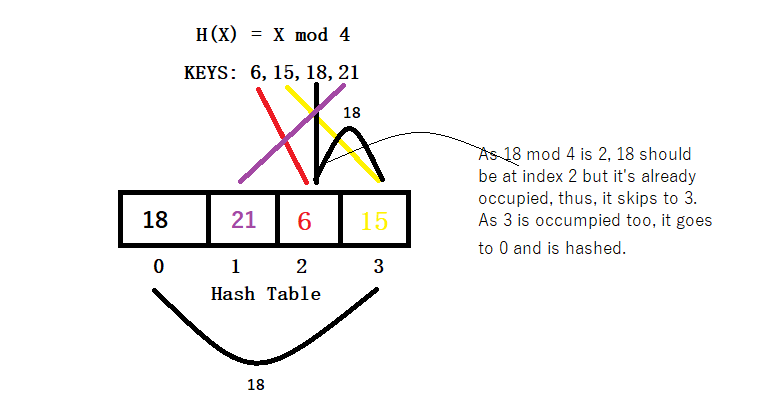
The answer for the above example will be [18, 21, 6, 15].

Note:

1. Consider ‘0’ based indexing.
Detailed explanation ( Input/output format, Notes, Images )
Input format: 
The first line of input contains an integer ‘T’ denoting the number of test cases.

The first line of each test case contains a positive integer ‘N’ representing the size of array KEYS.

The second line of each test case contains ‘N’ space-separated non-negative integers representing elements of the array KEYS.
Output format : 
For each test case, return an array 'HASH_TABLE’ of size ‘N’ where HASH_TABLE[ i ] is the element from the given array KEYS which is mapped to the index i.
Note: 
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints: 
1 <= T <= 10
1 <= N <= 500
0 <= KEYS[ i ] <= 10^9

Time limit: 1 sec
Sample Input 1:
2
5
5 3 2 6 4
4
1 5 3 7
Sample Output 1:
5 6 2 3 4
7 1 5 3
Explanation
For test case 1:
H(X) = X mod 5
All the numbers have unique hash values so there is no collision. Just map each index to its hash index.

For test case 2:
H(1) = 1L index 1 is unoccupied so we will map index 1 with 1.
H(5) = 1: but, index 1 is occupied, so, we will use index 2 which is unoccupied, and will map index 2 with 5.
H(3) = 3: index 3 is unoccupied so we will map index 3 with 3.
H(7) = 3, but index 3 is occupied so we will use index 0 which is unoccupied and will map index 0 with 7.
Sample Input 2:
2
6
4 7 8 1 2 5
3
6 7 10
Sample Output 2:
5 7 8 1 4 2
6 7 10
Hint

The approach is simple, just find the mapping index and if occupied, find the next available index.

Approaches (1)
Linear Probing

The approach is pretty simple. We just need to find the mapping index and if it is occupied, we need to search for the next available index.

 

The algorithm for the same is as follows:

  • Create an array HASH_TABLE of size N.
  • Initialise every value of HASH_TABLE as -1.
  • Loop for each KEY:
    • Initialize HASH = KEY % N
    • If HASH_TABLE[ HASH ] is already occupied, we perform:
      • while(HASH_TABLE[ HASH ] != -1):
        • HASH = ( HASH + 1 ) % N, iterating for valid hash index.
    • Update HASH_TABLE[ HASH ] with KEY.
  • Return HASH_TABLE
     

Let’s take an example of keys = { 91, 28, 46 }.

  • Initialise HASH_TABLE = { -1, -1, -1 }
  • For 91, H(91) = 91 mod 3 i.e. 1.
    • As index 1 is free, HASH_TABLE becomes { -1, 91, -1 }.
       
  • For 28, H(28) = 28 mod 3 i.e. 1.
    • As index 1 is already occupied, we will move to while loop:
      • We use index 2, which is free, HASH_TABLE becomes { -1, 91, 28 }
         
  • For 46, H(46) = 46 mod 3 i.e. 1.
    • As index 1 is occupied, we move to while loop:
    • HASH = (1 + 1) mod 3 i.e. 2. As index 2 is occupied, loop continues.
      • HASH = (2 + 1) mod 3 i.e. 0. Index 0 is free, thus, we will use index 0.

The final HASH_TABLE becomes { 46, 91, 28 }

Time Complexity

O(N * N) per test case where N is the size of the hashtable.

 

In the worst case, we will be traversing almost full hashtable for each key.

Space Complexity

O(1) per test case.

 

In the worst case, we are using constant extra space.

Code Solution
(100% EXP penalty)
Linear Probing
Full screen
Console