Problem

Submissions

Hints & solutions

Discuss

Longest Common Subsequence

Moderate

0/80

Average time to solve is 39m

Contributed by

242 upvotes

Asked in companies

Problem statement

Given two strings, 'S' and 'T' with lengths 'M' and 'N', find the length of the 'Longest Common Subsequence'.

For a string 'str'(per se) of length K, the subsequences are the strings containing characters in the same relative order as they are present in 'str,' but not necessarily contiguous. Subsequences contain all the strings of length varying from 0 to K.

Example :

Subsequences of string "abc" are:  ""(empty string), a, b, c, ab, bc, ac, abc.

Detailed explanation ( Input/output format, Notes, Images )

Input format :

The first line of input contains the string 'S' of length 'M'.

The second line of the input contains the string 'T' of length 'N'.

Output format :

Return the length of the Longest Common Subsequence.

Constraints :

0 <= M <= 10 ^ 3
0 <= N <= 10 ^ 3

Time Limit: 1 sec

Sample Input 1 :

adebc
dcadb

Sample Output 1 :

Explanation of the Sample Output 1 :

Both the strings contain a common subsequence 'adb', which is the longest common subsequence with length 3.

Sample Input 2 :

ab
defg

Sample Output 2 :

Explanation of the Sample Output 2 :

The only subsequence that is common to both the given strings is an empty string("") of length 0.

Hint 1

Hint 2

Hint 3

This problem has a lot of overlapping subproblems. Is there a way to compute the results of these subproblems at most once?

Approaches (3)

Approach 1

Approach 2

Approach 3

Memoization

Let the two strings be x and y.

Let x(i) be the substring of x from index 0 to index i.

Let c[i, j] be the length of the longest common subsequence of strings x(i) and y(j).

Then the recurrence relation to find c[i, j] is as follows:

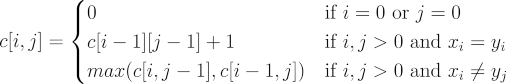
We can use this relation to write a simple recursive program but instead of recomputing the results of subproblems, compute them just once and store their results in a lookup table (Hashmap). Then whenever we would need to find the result of a subproblem, first we'll look for it in our table, if it's present then simply return it, otherwise use recursion to find the answer and then store it in the table.

Time Complexity

O(m * n), where m and n are the lengths of each string

We are maintaining a lookup table of size (m*n) and we will fill each cell of this table exactly once. Hence, total operations will be (m*n)

Space Complexity

O(m * n), where m and n are the lengths of each string

We are creating a lookup table of size (m*n)

(75% EXP penalty)

(100% EXP penalty)

Longest Common Subsequence

Console