Problem

Submissions

Hints & solutions

Discuss

Matrix Is Symmetric

Easy

0/40

Average time to solve is 10m

Contributed by

43 upvotes

Asked in companies

Problem statement

You are given a square matrix, return true if the matrix is symmetric otherwise return false.

A symmetric matrix is that matrix whose transpose is equal to the matrix itself.

Example of symmetric matrix :

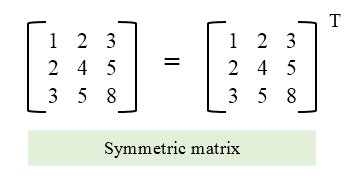
Detailed explanation ( Input/output format, Notes, Images )

Input Format:

The first line contains an Integer 'T' which denotes the number of test cases or queries to be run. Then the test cases follow.

The first line of each test case contains the size of the square matrix 'N'.

The second line of each test case contains the 'N' * 'N' Integers separated by a single space (the matrix is entered row-wise)

Output format :

For each test case/query, print whether the given matrix is symmetric or not.

Output for every test case will be printed in a separate line.

Note:

You do not need to print anything, it has already been taken care of. Just implement the given function.

Constraints:

1 <= T <= 10
1 <= N  <= 10^2
-10^9 <= data <= 10^9

Where 'data' denotes the element in the given 'matrix'.

Time Limit: 1 sec

Sample Input 1 :

1
3
1 2 3 2 4 5 3 5 8

Sample Output 1 :

Yes

Explanation For The Sample Output 1 :

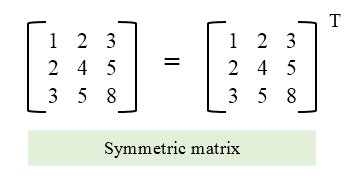
Sample Input 2 :

1
3
1 2 3 1 4 5 3 5 8

Sample Output 2 :

No

Explanation For The Sample Output 2 :

Hint 1

Hint 2

Try to create the transpose of the matrix.

Approaches (2)

Approach 1

Approach 2

Brute Force

Create another matrix ‘TRANSPOSE’ of the same size initially having all zeros.
Now replace ‘TRANSPOSE’ (i,j) with ‘MATRIX’ (j,i).
And now traverse both matrixes element by element if anywhere there is inequality return false, else continue.
In the end, return true as you traverse.

Time Complexity

O(N^2) , Where ‘N’ is the size of the square matrix.

Since every element is visited once and there are ‘N’ ^2 elements in total. Hence the overall time complexity is O(N^2).

Space Complexity

O(N ^ 2), Where ‘N’ is the size of the square matrix.

Since an extra matrix of size ‘N’ * ‘N’ is created while making transpose of the matrix. Hence overall space complexity is O(N * N).

(100% EXP penalty)

Matrix Is Symmetric

Console