Shortest Job First(Non - preemptive)

Moderate
0/80
Average time to solve is 25m
profile
Contributed by
11 upvotes
Asked in company
OYO

Problem statement

You are given ‘N’ processes with their respective process id, arrival time, and burst time. Your task is to schedule the given ‘N’ processes using the shortest job first scheduling algorithm and find their respective waiting time and turnaround time.

Shortest Job First is a scheduling algorithm in which the process having the shortest execution time is chosen for the subsequent execution. Here, you will implement a non - preemptive version (Non-preemptive Scheduling is a CPU scheduling technique in which the process takes the resource (CPU time) and holds it till the process gets terminated or is pushed to the waiting state. No process is interrupted until it is completed, and after that processor switches to another process). It significantly reduces the average waiting time for other processes awaiting execution.

For example:

1

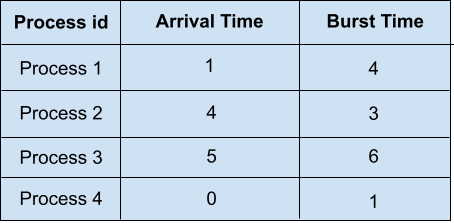
We have four processes in our ready queue. As we discussed, SJF will select the waiting process with the shortest execution time to execute next. So for the above example, the SJF scheduling of the processes along with their completion time, waiting time, and turnaround time will be,

1

Note:

1) Completion Time: Time at which process completes its execution.
2) Turn Around Time: Time difference between completion time and arrival time. Turn Around Time = Completion Time – Arrival Time.
3) Waiting Time(W.T.): Time difference between turn around time and the burst time. Waiting Time = Turn Around Time – Burst Time.
Detailed explanation ( Input/output format, Notes, Images )

Input Format:

The first line of input contains an integer 'T' representing the number of test cases.

The first line of each test case contains a single integer, ‘N’, where ‘N’ represents the number of processes.

The next ‘N’ lines of each test case containing three space-separated integers, ‘processId’, ‘arrivalTime’ and ‘burstTime’, where ‘processId’, ‘arrivalTime’ and ‘burstTime’ represents the process id, arrival time, and burst time for the processes, respectively.

Note: It is guaranteed that each process has a unique process id.

Output Format:

For each test case, print ‘N’ lines, each having five space-separated integers, process id, arrival time, burst time, waiting time, and turnaround time.

Print the processes according to SJF scheduling. If multiple processes have the same execution time, schedule the process with a lower process id first.

The output of each test case will be printed in a separate line.

Note:

You do not need to print anything, it has already been taken care of. Just implement the given function.

Constraints:

1 <= T <= 5
1 <= N <= 100
1 <= processId <= N
0 <= arrivalTime <= 10 ^ 7
1 <= burstTime <= 10 ^ 7

Where ‘T’ is the total number of test cases, ‘N’ denotes the number of processes,  ‘processId’, ‘arrivalTime’, and ‘burstTime’ represents the process id, arrival time, and burst time of any process, respectively.

Time Limit: 1 sec

Sample Input 1:

2
3
1 3 2
3 1 5
2 4 1
4
1 2 7
3 2 3
2 0 4
4 0 1

Sample Output 1:

3 1 5 0 5
2 4 1 2 3
1 3 2 4 6
4 0 1 0 1
2 0 4 1 5
3 2 3 3 6
1 2 7 6 13

Explanation Of Sample Input 1:

Test Case 1 :  
The process given is,

1

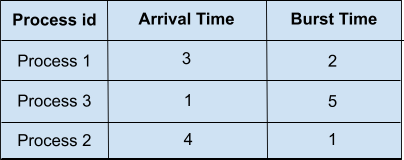
We have three processes in our ready queue. SJF will select the waiting process with the shortest execution time to execute next. The SJF scheduling of the processes along with their completion time, waiting time, and turnaround time will be,

1

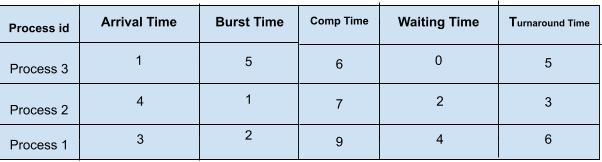
Test Case 2 : 
The process given is,

1 

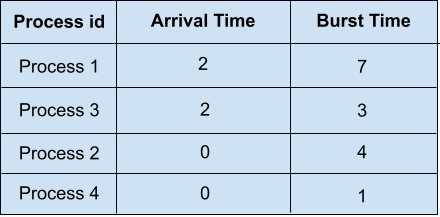
We have four processes in our ready queue. SJF will select the waiting process with the shortest execution time to execute next. The SJF scheduling of the processes along with their completion time, waiting time, and turnaround time will be,

1

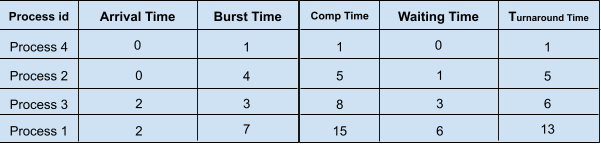
Sample Input 2:

1
4
1 4 1
4 3 2
2 2 3
3 1 4

Sample Output 2:

3 1 4 0 4
1 4 1 1 2
4 3 2 3 5
2 2 3 6 9

Explanation of Sample Input 2:

Test Case 1 :  
The process given is,

1 

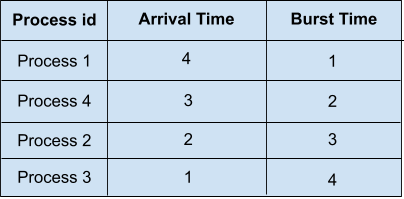
We have four processes in our ready queue. SJF will select the waiting process with the shortest execution time to execute next. The SJF scheduling of the processes along with their completion time, waiting time, and turnaround time will be,

1

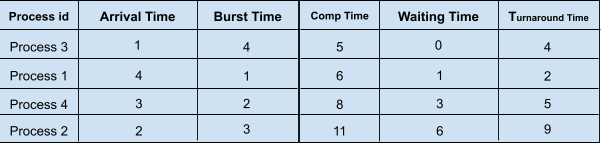
Hint

Try to build a constructive algorithm.

Approaches (1)
Shortest Job First Algorithm

Approach: The idea here is to sort the given ‘N’ processes in increasing order of their arrival times. For the processes with the same arrival time, we will sort them in increasing order of burst time. We will iterate through all the processes from left to right, and for any process ‘i’, where ‘i’ is from 0 to ‘N’ - 1, we will find all the processes whose arrival time is less than or equal to the completion time of the i-th process. Among all those processes, we will take the process with minimum burst time, and we will swap it with the i-th process, as this process has a lower execution time than the i-th process. Simultaneously we will compute the completion time, waiting time, and turnaround time for each process.

 

Algorithm:
 

  1. Declare a 2 - Dimensional array, say ‘PROCESSDETAILS’ of size ‘N’ * 6, to store the process id, arrival time, burst time, completion time, waiting time, and turnaround time, respectively, for each process.
  2. Run a loop for ‘i’ from 0 to ‘N’ - 1.
  3. Insert ‘PROCESSID’, ‘ARRIVALTIME’, and ‘BURSTTIME’ of the i-th process into ‘PROCESSDETAILS’.
  4. Sort ‘PROCESSDETAILS’ in increasing order of arrival time. If arrival time is the same, sort it in increasing order of burst time. If both arrival time and burst time are the same, sort it in increasing process id.
  5. Assign completion time, turnaround time, and waiting time for the first process in ‘PROCESSDETAILS’ as
    • ‘PROCESSDETAILS[0][3]’ = ‘PROCESSDETAILS[0][1]’ + ‘PROCESSDETAILS[0][2]’
    • ‘PROCESSDETAILS[0][5]’ = ‘PROCESSDETAILS[0][3]’ - ‘PROCESSDETAILS[0][1]’
    • ‘PROCESSDETAILS[0][4]’ = ‘PROCESSDETAILS[0][5]’ - ‘PROCESSDETAILS[0][2]’
  6. Run a loop for ‘i’ from 1 to ‘N’ - 1.
    • Declare an integer, say ‘PREVCOMPTIME’, to store the completion time of the previous process and initialize it with ‘PROCESSDETAILS[i - 1][3]’
    • Declare an integer, say ‘CURRBURSTTIME’, to store the minimum burst time of any process whose arrival time is less than or equal to ‘PREVCOMPTIME’ and initialize it with ‘PROCESSDETAILS[i][2]’.
    • Declare an integer, say ‘CURRID’, to store the process id of any process whose arrival time is less than or equal to ‘PREVCOMPTIME’ and has minimum burst time and process id, initialize it with ‘PROCESSDETAILS[i][0]’.
    • Declare an integer, say ‘index’ to store the index of the process with minimum burst time, and initialize it with ‘i’.
    • Run a loop for ‘j’ from ‘i’ to ‘N’ - 1
      • If ‘PROCESSDETAILS[j][1]’ is less than or equal to ‘PREVCOMPTIME’
        • If ‘PROCESSDETAILS[j][2]’ is less than ‘CURRBURSTTIME’
          • Update ‘CURRBURSTTIME’ as ‘CURRBURSTTIME’ = ‘PROCESSDETAILS[j][2]’.
          • Update ‘CURRID’ as ‘CURRID’ = ‘processDetails[j][0].
          • Assign ‘j’ to ‘INDEX’ i.e., do ‘INDEX’ = j.
        • Else if ‘PROCESSDETAILS[j][2]’ is equal to ‘CURRBURSTTIME’ and ‘processDetails[j][0]’ is less than ‘CURRID’
          • Update ‘CURRID’ as ‘CURRID’ = ‘PROCESSDETAILS[j][0].
          • Assign ‘j’ to ‘INDEX’ i.e., do ‘INDEX’ = j.
    • Assign completion time, turnaround time, and waiting time for the process in ‘PROCESSDETAILS’ at ‘INDEX’ as
      • ‘PROCESSDETAILS[INDEX][3]’ = ‘PREVCOMPTIME’ + ‘PROCESSDETAILS[INDEX][2]’
      • ‘PROCESSDETAILS[INDEX][5]’ = ‘PROCESSDETAILS[INDEX][3]’ - ‘processDetails[INDEX][1]’
      • ‘PROCESSDETAILS[INDEX][4]’ = ‘PROCESSDETAILS[INDEX][5]’ - ‘PROCESSDETAILS[INDEX][2]’.
    • Swap ‘PROCESSDETAILS[INDEX]’ and ‘PROCESSDETAILS[i]’.
  7. Declare a 2 - Dimensional array, say ‘ANSWER’ of size ‘N’ * 5, to store the process id, arrival time, burst time, waiting time, and turnaround time, respectively, for each process.
  8. Run a loop for ‘i’ from 0 to ‘N’ - 1
    • Insert ‘PROCESSDETAILS[i][0]’, ‘PROCESSDETAILS[i][1]’, ‘PROCESSDETAILS[i][2]’, ‘PROCESSDETAILS[i][4]’, and ‘PROCESSDETAILS[i][5]’ into ‘answer’, as we don’t need to return completion time of any process.
  9. Return ‘ANSWER’.
Time Complexity

O(N ^ 2), where ‘N’ denotes the number of processes.

 

We sort ‘processDetails’ which takes O(N * log(N)) time. Also, we iterate through all the ‘N’ processes, and for each process, we iterate over all the remaining processes to find a process with a minimum execution time that takes O(N) * O(N) = O(N ^ 2) time. Therefore, the total time complexity will be O(N * log(N)) + O(N ^ 2), which is the same as O(N ^ 2).

Space Complexity

O(N), where ‘N’ denotes the number of processes.

 

We create a 2 - Dimensional array of integers, ‘processDetails’, which takes O(N) space. 

Sorting the array ‘processDetails’ takes O(log(N)) space. Also, we create a 2 - dimensional array of integers, ‘answer’, which takes O(N) space. Therefore, the total space complexity will be O(log(N)) + O(N) + O(N), which is O(N).

Code Solution
(100% EXP penalty)
Shortest Job First(Non - preemptive)
Full screen
Console