Problem
Submissions
Hints & solutions
Discuss
Tiling Problem
Hard
0/120
Average time to solve is 45m
Problem statement
You have been given a board where there are '2' rows and 'N' columns. You have an infinite supply of 2x1 tiles, and you can place a tile in the following ways:
1. Horizontally as 1x2 tile
2. Vertically as 2x1 tile
Count the number of ways to tile the given board using the available tiles.
Note :The number of ways might be large so output your answer modulo 10^9 + 7.
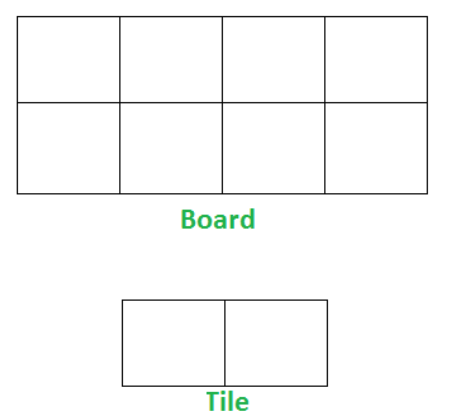
Here an example of tile and board for 'N' = 4 :
Detailed explanation ( Input/output format, Notes, Images )
Input format :
The first and only line of each test case contains an Integer 'N' which denotes the size of the board, i.e. '2' rows and 'N' columns.
For each test case, print the number of ways to tile the board modulo 10^9 + 7.
You are not required to print the output explicitly, it has already been taken care of. Just implement the function.
Constraints :
1 <= N <= 10^18
Where 'N' is the number of columns in the board.
Time limit: 1 sec
Sample Input 1 :
3
Sample Output 1 :
3
Explanation to Sample Input 1 :
For a 2*3 board, there are three ways:
1. Place all 3 tiles vertically.
2. Place first tile vertically and remaining 2 tiles horizontally.
3. Place first 2 tiles horizontally and remaining tiles vertically.
Sample Input 2 :
4
Sample Output 2 :
5
Explanation to Sample Input 2 :
For a 2*4 board, there are five ways:
1. All 4 vertical
2. All 4 horizontal
3. First 2 vertical, remaining 2 horizontal
4. First 2 horizontal, remaining 2 vertical
5. Corner 2 vertical, middle 2 horizontal
Hint
Hint 1
Hint 2
Hint 3
Try to explore the possibilities of placing tiles to get the number of ways from smaller sub-problems.
Approaches (3)
Approach 1
Approach 2
Approach 3
Recursion And Memoization (Runtime error)
Try to place the tile to fill the unit column and calculate the number of ways from smaller sub-problems. Then use memoization to convert O(2^N) solution to an O(N) solution.
- At any point we are at ‘idx’ column then we can place our tile in two ways to fill this column.
- Option 1 - 1 Horizontal Tile
We can place in this way where we have ‘idx-1’ column filled.
2. Option 2 - 2 Vertical Tiles
We can place in this way where we have ‘idx-2’ column filled.
2. So, numberOfWays(n) = numberOfWays(n-1) + numberOfWays(n-2)
3. Base cases are:
- When n = 1 there is only 1 way - Placing 1 Vertical Tile
- When n = 2 there are two ways - Placing 2 Vertical Tile and Placing 2 Horizontal Tiles.
- Also, take care of overflow using modulo 10^9 + 7.
- Lastly, use a DP Array of size N for memoization to save time over repetitive calls.
Time Complexity
O(N), where N is the number of columns in the board.
As we are using the Dynamic Programming Approach and at max, we can have N different calls so, Overall Time Complexity is O(N).
Space Complexity
O(N), where N is the number of columns in the board.
We are using DP Matrix of Space Complexity O(N) to store solutions. Hence, the overall Space Complexity is O(N).
Code Solution
(100% EXP penalty)
Tiling Problem
Javascript (node v10.20.0)
Console




