Trapping Rain Water ll

Hard
0/120
Average time to solve is 45m
profile
Contributed by
9 upvotes
Asked in companies
GoogleShareChatAmazon

Problem statement

Given an M * N matrix, where the value at any cell denotes the height of that cell in a 2-D elevation map. You need to find the volume of water that can be trapped within it.

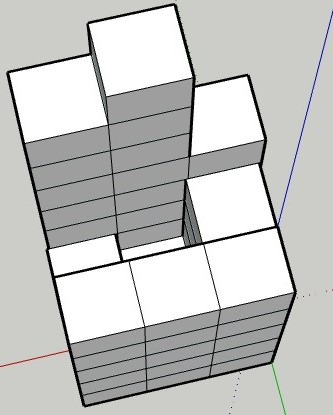
For a matrix = 
[ 5, 5, 5 ]
[ 5, 2, 3 ]
[ 6, 9, 8 ]  

2-D elevation map will look like this

2-D map

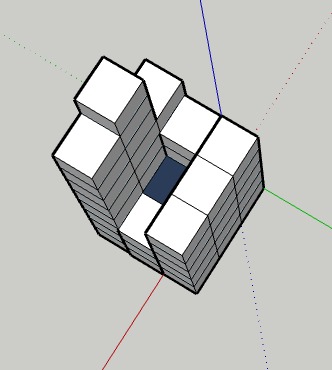
After the rain, a total of 1 unit volume of water gets trapped, and this 2-D elevation map will look like this

After rain

Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line contains a single integer ‘T’ denoting the number of test cases.

The first line of each test case contains two space-separated integers ‘M’ and ‘N’ denoting the number of rows and columns in the matrix.

The next ‘M’ lines contain ‘N’ space-separated integers denoting the height of each cell.
Output Format: 
For each test case, print a single integer denoting the volume of water that can be trapped.

Print the output of each test case in a separated line.
Note: 
You don't need to print anything, it has already been taken care of. Just implement the given function.
Constraints: 
1 <= T <= 10
1 <= M,N <= 100
1 <= matrix[i][j] <= 10^3

Where ‘T’ is the number of test cases, ‘M’ and ‘N’ are the dimensions of the given matrix.
Matrix[i][j] is the height of the cell at the ‘i-th’ row and ‘j-th’ column.

Time Limit: 1 sec.
Sample Input 1:
2
3 3
5 5 5
5 2 3
6 9 8
5 4
10 11 1 10
11 2 11 10
11 6 8 10
10 11 10 10
11 11 11 11
Sample Output 1:
1
14
Explanation For Sample Input 1:
Test Case 1: Only 1 unit volume of water can be trapped between cells with height ‘3’ and ‘2’. 

Test Case 2: ‘2’ unit of volume will be stored between matrix [ 2 ][ 2 ] and matrix[ 2 ][ 3 ].
‘4’ unit of volume will be stored between matrix [ 2 ][ 1 ] and matrix[ 2 ][ 3 ].
‘8’ units of volume will be stored between matrix [ 1 ][ 1 ] and matrix[ 2 ][ 3 ].
Therefore a total of ‘14’ unit volume will be trapped.
Sample Input 2:
2
2 4
3 8 9 2
2 5 7 1
4 4
4 12 8 6
2 1 5 13
2 1 12 7
2 2 10 5
Sample Output 2:
0
2
Explanation For Sample Input 2:
Test Case 1: They only have two sides. Thus, to accommodate any water it needs 4 edges. So, no units of water can be trapped between sides.

Test Case 2: ‘1’ unit of volume will be stored between matrix [ 2 ][ 1 ] and matrix[ 2 ][ 2 ].
‘2’ unit of volume will be stored between matrix [ 3 ][ 1 ] and matrix[ 3 ][ 3 ].
Therefore a total of ‘2’ unit volume will be trapped.
Hint

Can you think of solving it with using breath first search like algorithm?

Approaches (1)
Priority Queue Implementation.

Approach: The border cells can never hold water as water will always flow out from there. So we will assume all the border cells as our boundary.

 

Now the water that can behold at least inside the cells will be equal to the minimum height of the boundary.

 

For eg if matrix = [ 8, 8, 8, 8 ]

                            [ 6, x, x, 8 ]

                            [ 6, x, x, 5 ]

                            [ 6, 8, 8, 8 ]

 

Now if any cell holds water > mat[ 2 ][ 3 ] then it can flow out. So if any of the cells have a height less than ‘5’ then it can trap utmost ‘5’ volume water in it.

 

We have to maintain this minimum border height also so that it can be determined what volume of water we can store. 


So the basic idea is we will find the boundary cell having minimum height. If any of its neighbor cells have a height less than the minimum border height then it can store water = difference between the height of cells and minimum border height Otherwise all the neighboring cells will be considered as boundary cells.


We will take a priority queue that will store the cell positions based on the height of each cell.

Initially, we will visit all the boundary cells and put them in the queue.

Now the front element of the queue will give the cell a minimum height. 

Now visit the neighbors of the boundary cell having minimum height. Push all the neighbors to queue. If any cell has a height smaller than this boundary cell then it can trap water = difference between heights of this cell and minimum border height.


Whenever a front element of the queue is popped out, if the cell has a height of more than the minimum border height, then we will update the minimum border height.

 

Algorithm:

 

  1. Initialize a ‘VISITED’ array that will keep track of all the visited cells.
  2. Create a priority queue ‘Q’ that will store pair of ( int and pair<int, int> )
  3. Take a variable ‘RES’ to store the result.
  4. Push all the border cells in the ‘Q’ and mark them as visited.
  5. Take a variable ‘MINBH’ that will store minimum border height.
  6. Run a loop while ‘Q’ is not empty.
    • Store the height of the top cell of ‘Q’ in ‘CURRENTH’
    • Store the coordinates of the top cell in ‘Q’ in ‘CURRENTX’ and ‘CURRENTY’.
    • Update ‘MINBH’ as max of ‘MINBH’ and ‘CURRENTH’.
    • Pop this top cell from ‘Q’
    • Initialize a 2-D matrix ‘directions’ with values [ [ 0 1 ] , [ 0 -1 ] [ 1 0 ] [ -1 0 ] ] to visit all the neighbouring cells.
    • Run a loop 'i' from 0 to 3 for all the directions.
      • NEWX = CURRENTX + DIRECTIONS[ i ][ 0 ]
      • NEWY = CURRENTY + DIRECTIONS[ i ][ 1 ]
      • If the cell at coordinates ‘NEWX’ and ‘NEWY’ is a valid cell and it is not visited yet, then push this cell to ‘Q’ and mark it as visited.
      • If the height of this cell at ‘NEWX’ and ‘NEWY’ is less than ‘MINBH’ then add (MINBH - MAT[ NEWX][ NEWY]) to ‘RES’
  7. Return ‘RES’.
Time Complexity

O( M*N *log(M*N) ), where ‘M’ and ‘N’ are the dimensions of the given matrix.

 

We are maintaining a priority queue and inserting every cell of the matrix in it. Inserting M*N values in the priority queue will result in O( M*N *log(M*N) ) time complexity. 

Space Complexity

O( M*N ), where ‘M’ and ‘N’ are the dimensions of the given matrix.

 

We are using a priority queue that will store the cells of the matrix. So the space complexity is O(M*N).

Code Solution
(100% EXP penalty)
Trapping Rain Water ll
Full screen
Console