Binary Search Tree (BST)
Introduction
- These are specific types of binary trees.
- These are inspired by the binary search algorithm that elements on the left side of a particular element are smaller and that on the right side are greater.
- Time complexity on insertion, deletion, and searching reduces significantly as it works on the principle of binary search rather than linear search, as in the case of normal binary trees (will discuss it further).
How are BSTs stored?
In BSTs, we always insert the node with smaller data towards the left side of the compared node and the larger data node as its right child. To be more concise, consider the root node of BST to be N, then:
- Everything lesser than N will be placed in the left subtree.
- Everything greater than N will be placed in the right subtree.
For Example: Insert {45, 68, 35, 42, 15, 64, 78} in a BST in the order they are given.
Solution: Follow the steps below:
Since the tree is empty, so the first node will automatically be the root node.

Now, we have to insert 68, which is greater than 45, so it will go on the right side of the root node.
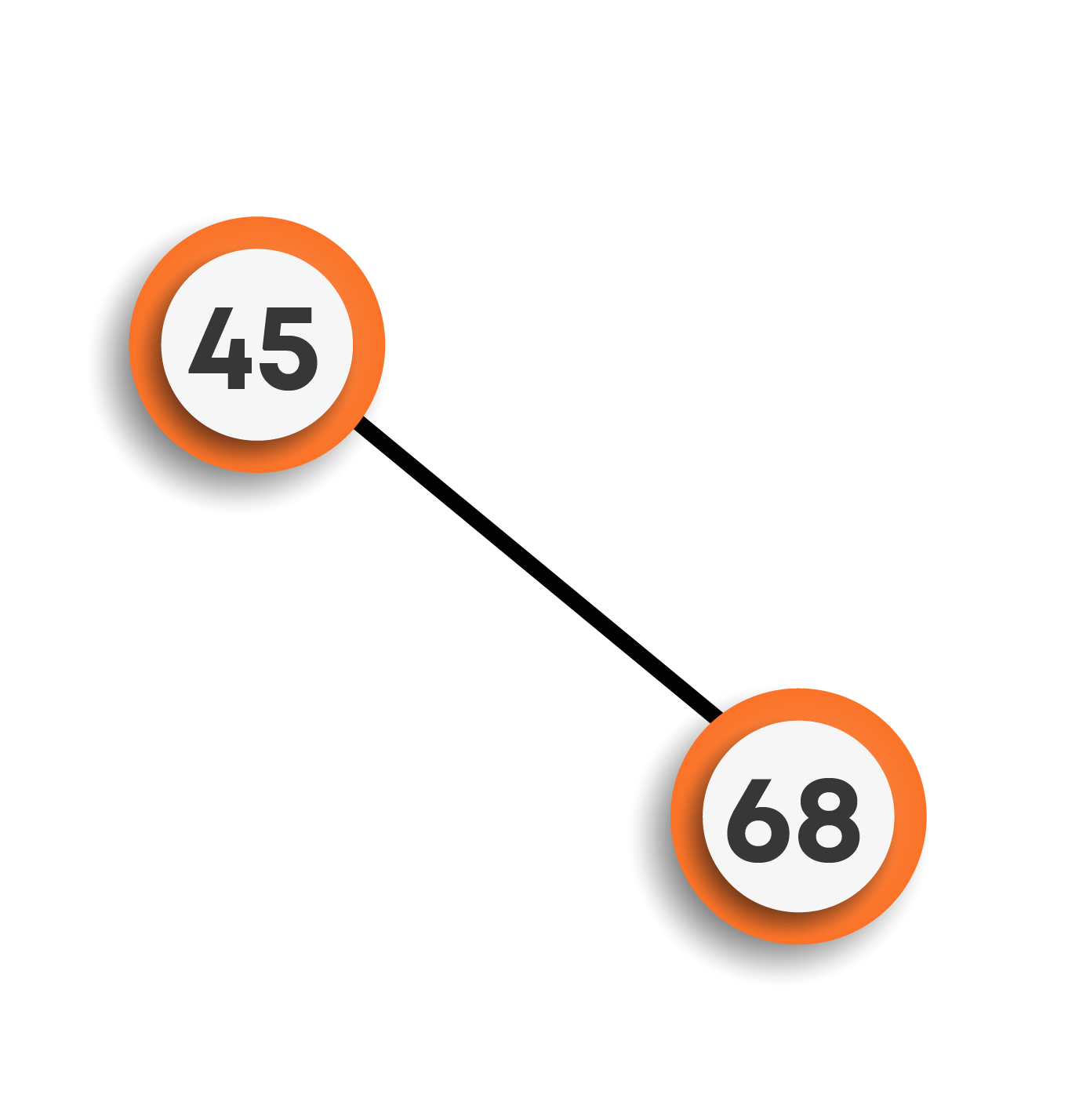
To insert 35, we will start from the root node. Since 35 is smaller than 45, it will be inserted on the left side.
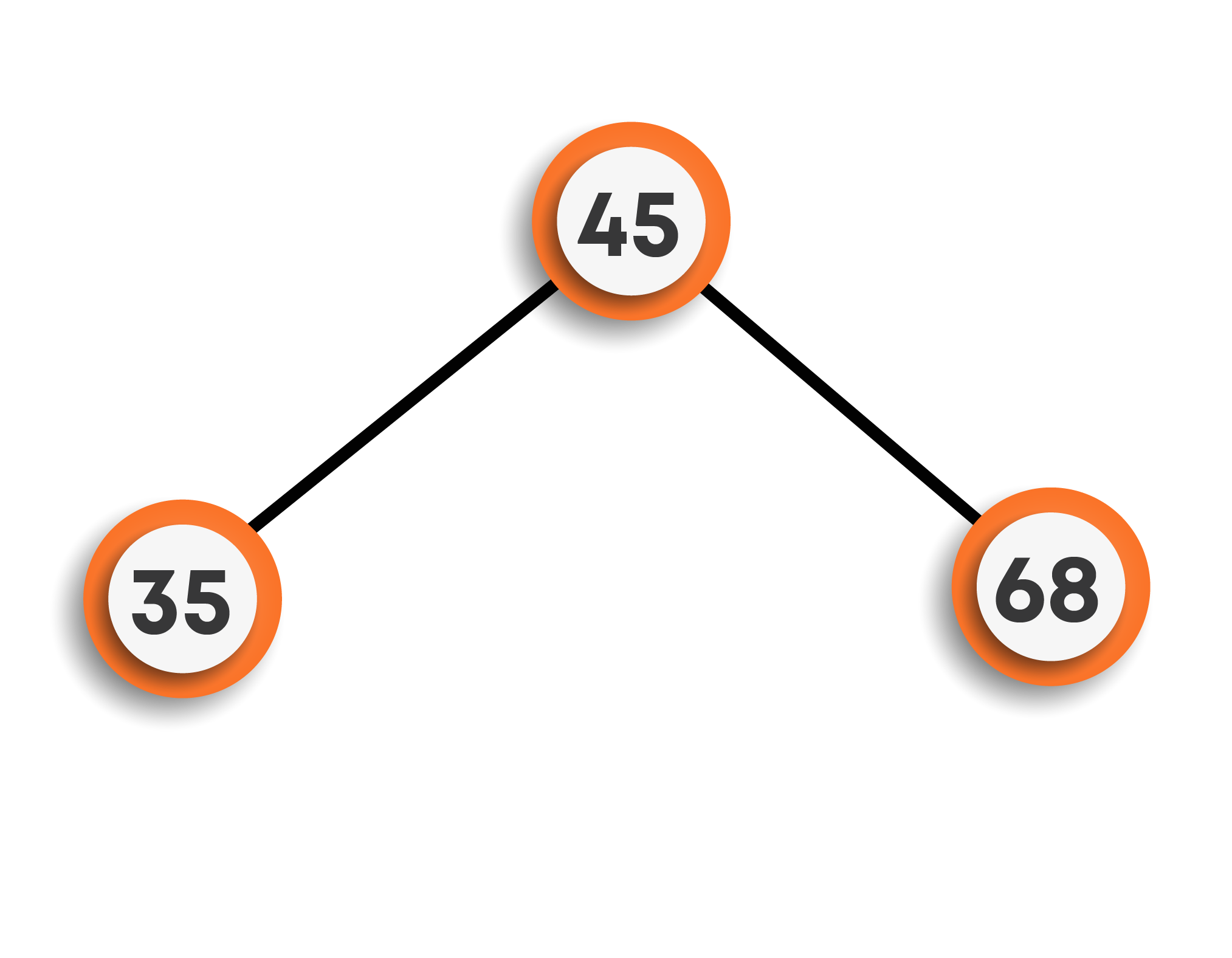
Moving on to inserting 42, we can see that 42 is less than 45 so it will be placed on the left side of the root node. Now, we will check the same on the left subtree. We can see that 42 > 35, this means 42 will be the right child of 35, which is still a part of the left subtree of the root node.
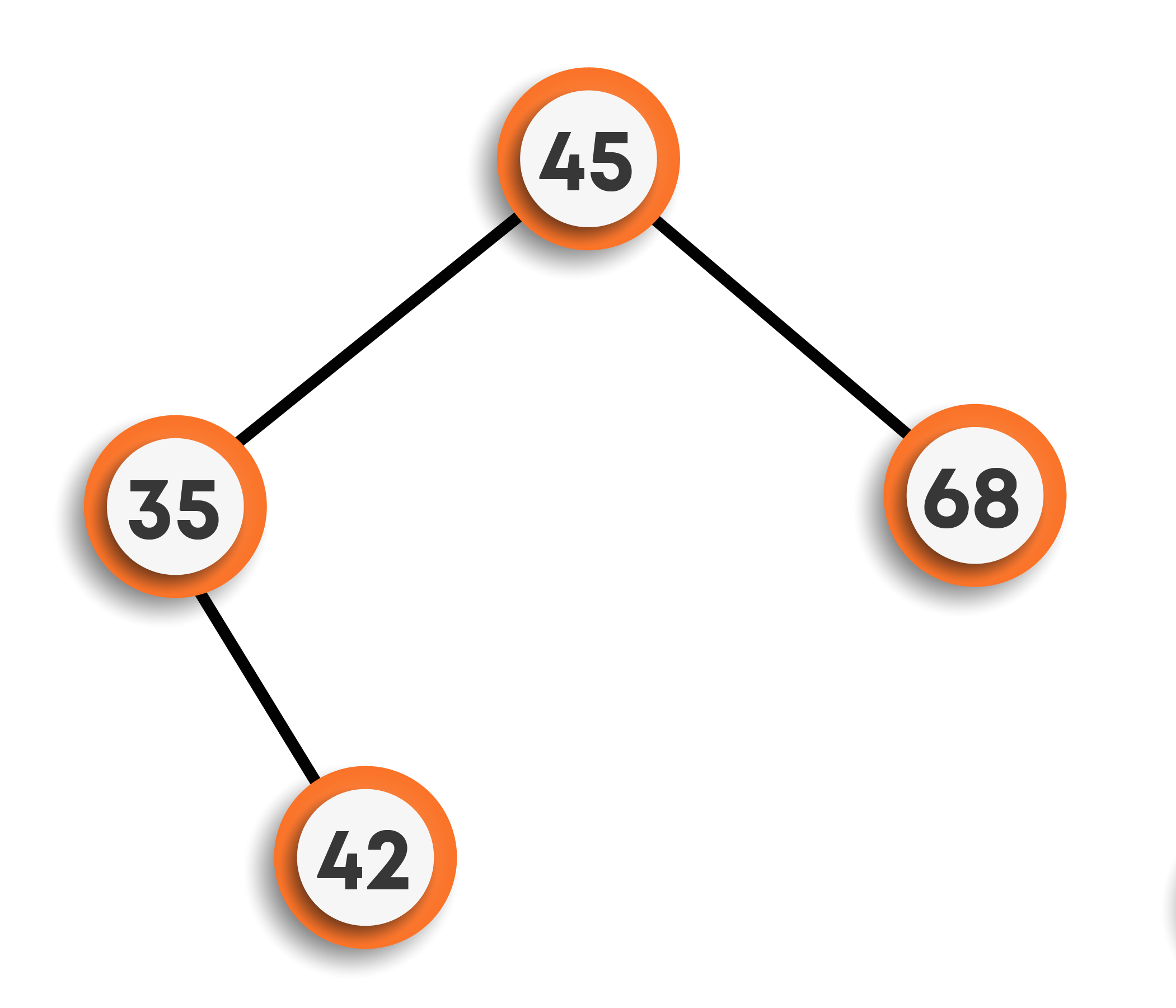
Now, on inserting 15, we will follow the same approach starting from the root node. Here, 15 < 45, means left subtree. Again, 15 < 35, means continue to move towards the left. As the left subtree of 35 is empty, so 15 will be the left child of 35.
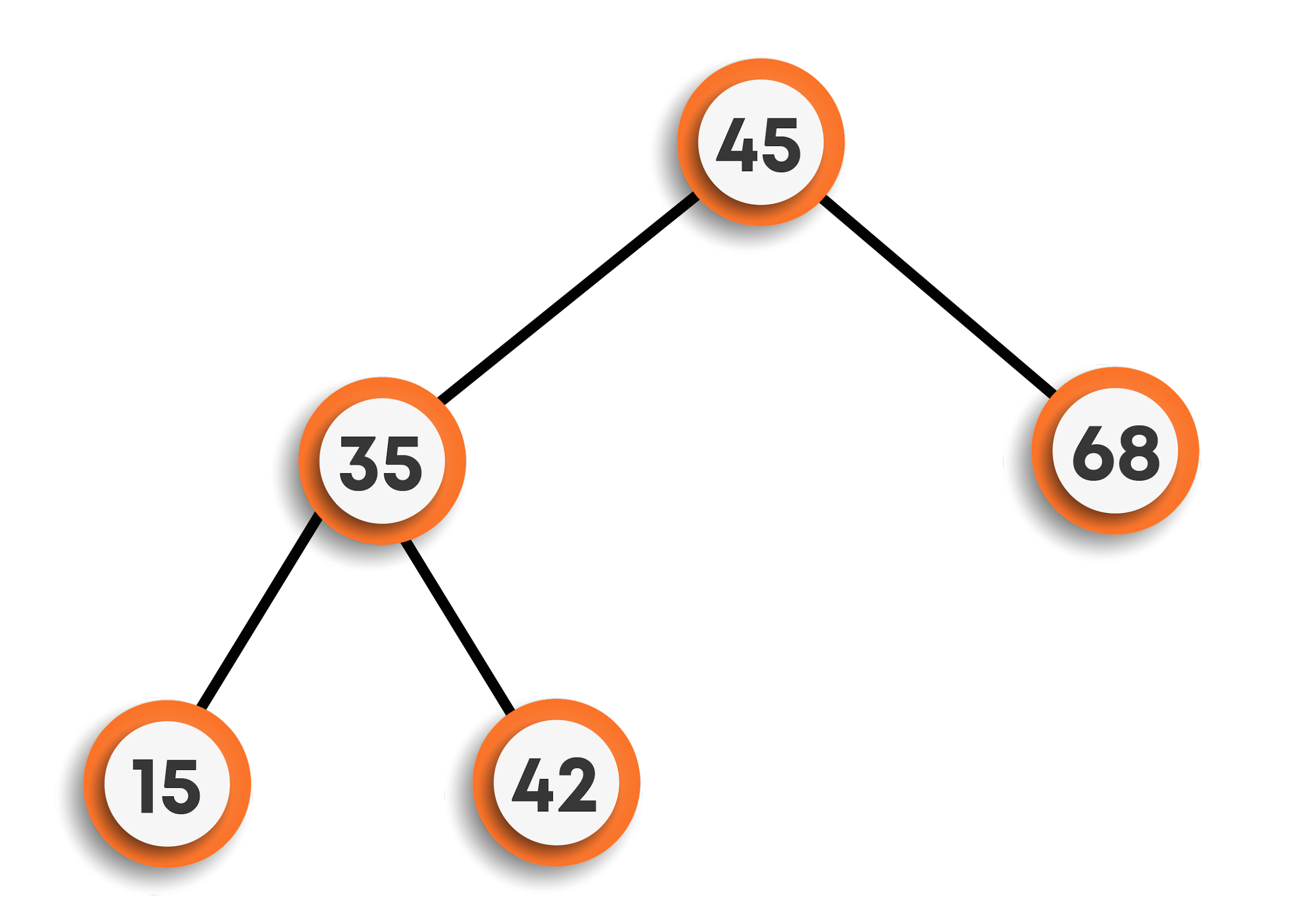
Continuing further, to insert 64, now we found 64 > root node’s data but less than 68, hence will be the left child of 68.
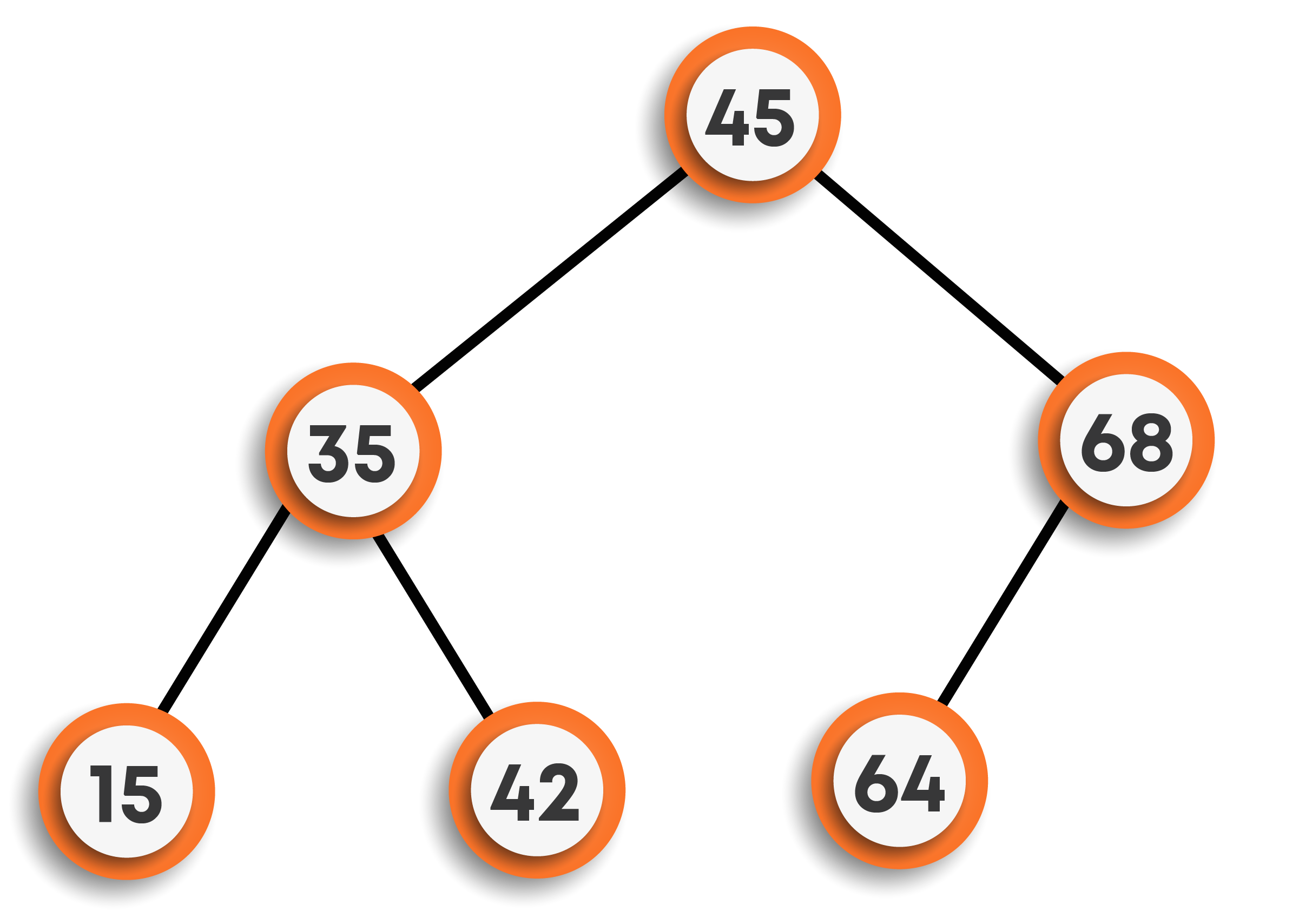
Finally, inserting 78, we can see that 78 > 45 and 78 > 68, so will be the right child of 68.
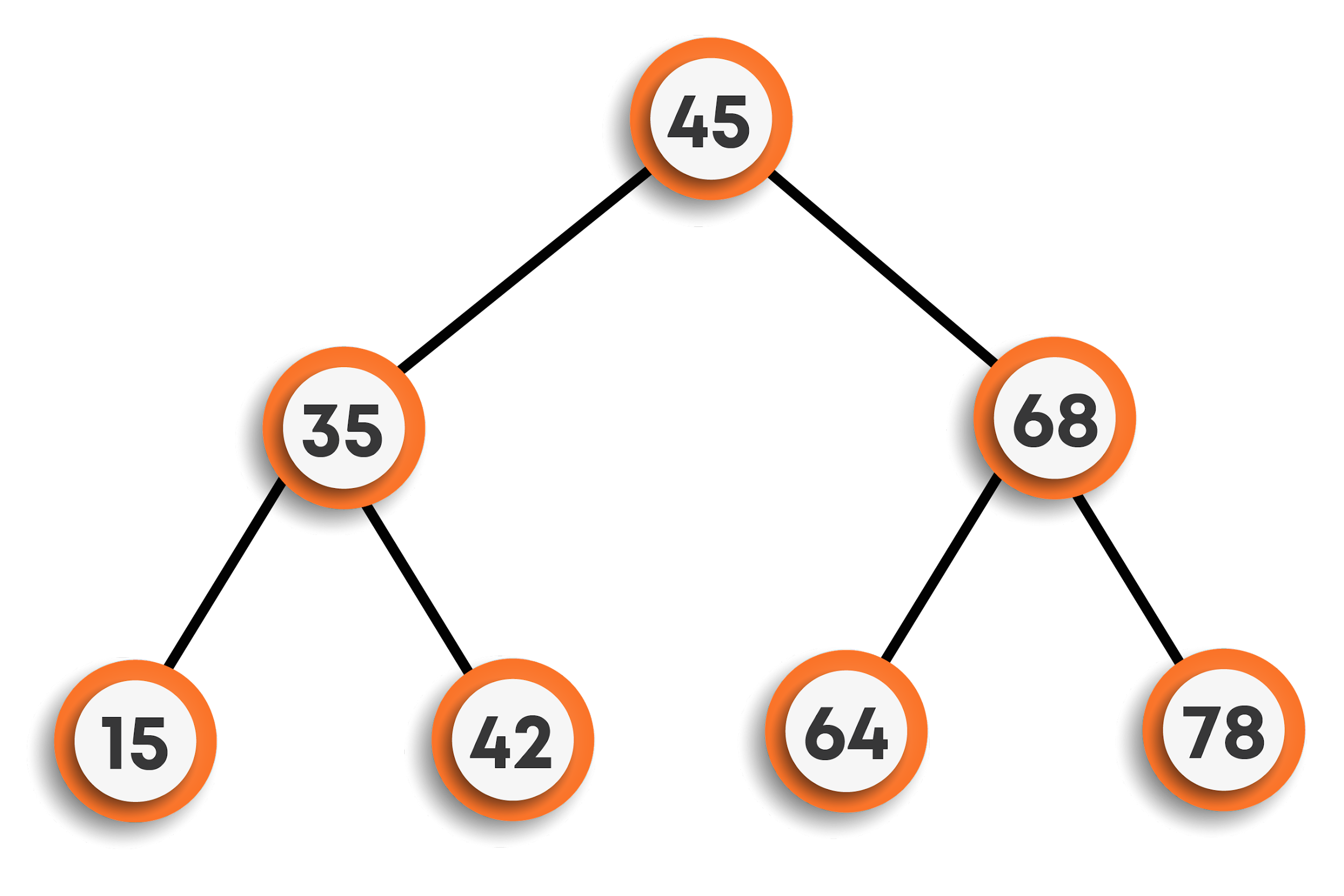
In this way, the data is stored in a BST.
If we follow the inorder traversal of the final BST, we will get all the elements in sorted order, hence to search we can now directly apply the binary search algorithm technique over it to search for any particular data.
As seen above, to insert an element, depending on the value of the element, we will either traverse the left subtree or right subtree of a node ignoring the other half straight away each time, till we reach a leaf node. Hence, the time complexity of insertion for each node is O(h) (where h is the height of the BST).
For inserting n nodes, the time complexity will be O(nh).
Note: The value of h is equal to logn on average, but can go to O(n) in the worst case (in the case of skew trees).
Applications
- They are used to implement hashmaps and tree sets.
- They are used to implement dictionaries in various programming languages.
- They are also used to implement multi-level indexing in Databases.
Operations in BST
Search in BST:
Given a value, we want to find out whether it is present in the BST or not.
Steps for search in the BST
- Visit the root.
- If it is null return false.
- If it is equal to value return true.
- If the value is less than the root’s data search in the left subtree else search in the right subtree.
function search(root, val)
if root is null
return false
/*
If the current node’s data is equal to val, then return true
Else call the function for left and right subtree depending on
the value of val
*/
if root.data equals val
return true
if val < root.data
return search(root.left, val)
return search(root.right, val)
Insertion in BST:
Given a value, we want to insert it into the BST. We will assume that the value is already not present in the tree.
Steps for insert in the BST
- Visit the root.
- If it is null, create a new node with this value and return it.
- If the value is less than the root’s data insert in the left subtree else insert in the right subtree.
function insert(root, val)
if root is null
/*
We have reached the correct place so we create a new
node with data val
*/
temp = newNode(val)
return temp
/*
else we recursively insert to the left and the right subtree
depending on the val
*/
if val < root.data
root.left = insert(root.left, val)
else
root.right = insert(root.right, val)
Deletion in BST:
Given a value, we want to delete it from the BST if present.
Steps for delete in the BST
- Visit the root.
- If root is null, return null
- If the value is greater than the root’s data, delete in the right subtree.
- If the value is lesser than the root’s data, delete in the left subtree.
- If the value is equal to the root’s data, then
- if it is a leaf, then delete it and return null.
- if it has only one child, then return that single child.
- else replace the root’s data with the minimum in the right subtree and then delete that minimum valued node.
function deleteData(data, root)
// Base case
if root == is null
return null
// Finding that root by traversing the tree
if (data > root.data)
root.right = deleteData(data, root.right)
return root
else if (data < root.data)
root.left = deleteData(data, root.left)
return root
// found the node with val as data
else
if (root.left == null and root.right == null)
// Leaf
delete root
return null
else if (root.left == null)
// root having only right child
return root.right
else if (root.right == null)
// root having only left child
return root.left
else
// root having both the childs
minNode = root.right;
// finding the minimum node in the right subtree
while (minNode.left != null)
minNode= minNode.left
rightMin = minNode.data
root.data = rightMin
// now deleting that replaced node using recursion
root.right = deleteData(rightMin, root.right)
return root
The time complexity of various operations:
If n is the total number of nodes in a BST, and h is the height of the tree (which is equal to O(logn) on average and can be O(n) in worst case i.e. skew trees ), then the time complexities of various operations for a single node in the worst case are as follows :
