Introduction to Recursion
Any function which calls itself is called recursion. A recursive method solves a problem by calling a copy of itself to work on a smaller problem. Each time a function calls itself with a slightly simpler version of the original problem. This sequence of smaller problems must eventually converge on a base case.
Working of recursion
We can define the steps of the recursive approach by summarizing the above three steps:
- Base case: A recursive function must have a terminating condition at which the process will stop calling itself. Such a case is known as the base case. In the absence of a base case, it will keep calling itself and get stuck in an infinite loop. Soon, the recursion depth* will be exceeded and it will throw an error.
- Recursive call (Smaller problem): The recursive function will invoke itself on a smaller version of the main problem. We need to be careful while writing this step as it is crucial to correctly figure out what your smaller problem is.
- Self-work : Generally, we perform a calculation step in each recursive call. We can achieve this calculation step before or after the recursive call depending upon the nature of the problem.
Note*: Recursion uses an in-built stack that stores recursive calls. Hence, the number of recursive calls must be as small as possible to avoid memory-overflow. If the number of recursion calls exceeded the maximum permissible amount, the recursion depth* will be exceeded. This condition is called stack overflow.
Now, let us see how to solve a few common problems using Recursion.
Problem Statement - Find Factorial of a number n.
Factorial of any number n is defined as n! = n * (n-1) * (n-2) * … *1. Ex: 5! = 5 * 4 * 3 * 2 * 1 = 120;
Let n = 5 ;
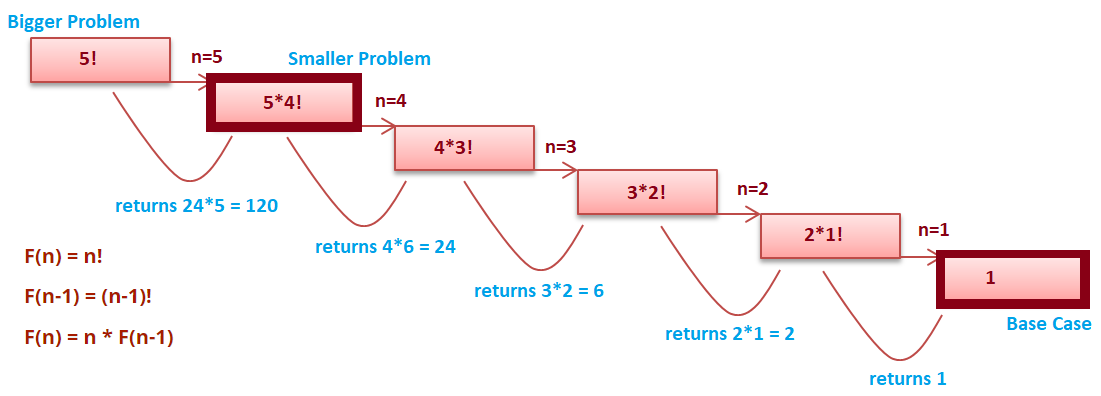
In recursion, the idea is that we represent a problem in terms of smaller problems. We know that 5! = 5 * 4!. Let’s assume that recursion will give us an answer of 4!. Now to get the solution to our problem will become 5 * (the answer of the recursive call).
Similarly, when we give a recursive call for 4!; recursion will give us an answer of 3!. Since the same work is done in all these steps we write only one function and give it a call recursively. Now, what if there is no base case? Let's say 1! Will give a call to 0!; 0! will give a call to -1! (doesn’t exist) and so on. Soon the function call stack will be full of method calls and give an error Stack Overflow. To avoid this we need a base case. So in the base case, we put our own solution to one of the smaller problems.
function factorial(n)
// base case
if n equals 0
return 1
// getting answer of the smaller problem
recursionResult = factorial(n-1)
// self work
ans = n * recursionResult
return ans
Problem Statement - Find nth fibonacci.
We know that Fibonacci numbers are defined as follows
fibo(n) = n for n <= 1
fibo(n) = fibo (n - 1) + fibo (n - 2) otherwise
Let n = 4
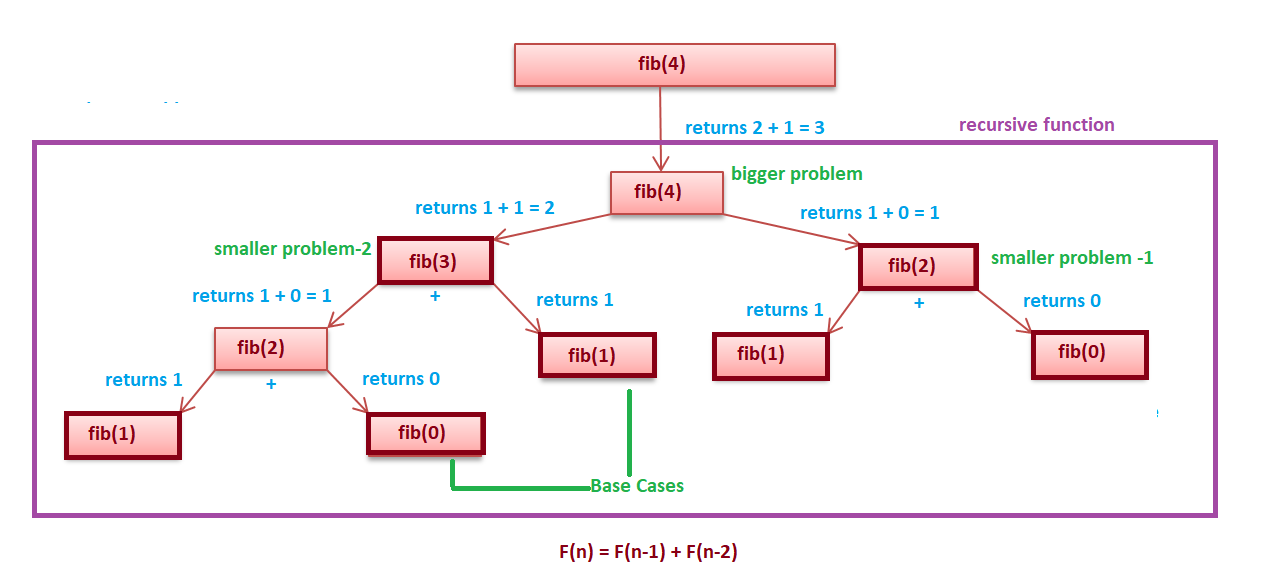
As you can see from the above fig and recursive equation that the bigger problem is dependent on 2 smaller problems.
Depending upon the question, the bigger problem can depend on N number of smaller problems.
function fibonacci(n)
// base case
if n equals 1 OR 0
return n
// getting answer of the smaller problem
recursionResult1 = fibonacci(n - 1)
recursionResult2 = fibonacci(n - 2)
// self work
ans = recursionResult1 + recursionResult2
return ans
Problem Statement - Check if an array is sorted
For example:
- If the array is {2, 4, 8, 9, 9, 15}, then the output should be true.
- If the array is {5, 8, 2, 9, 3}, then the output should be false.
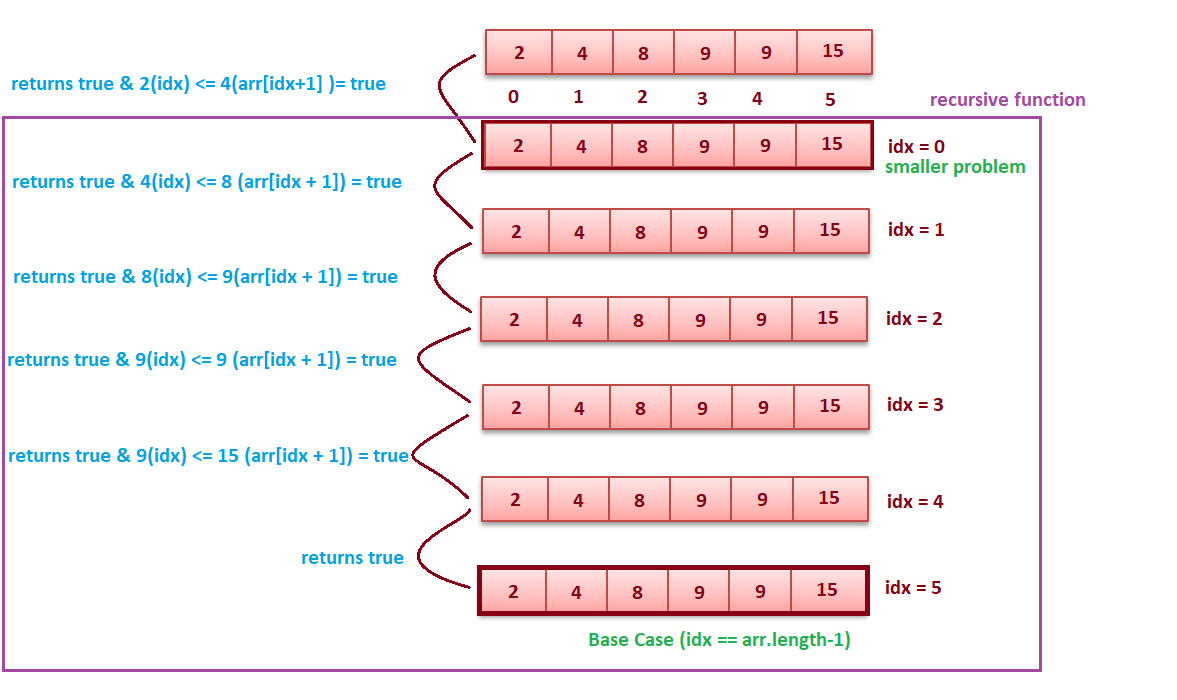
function isArraySorted(arr, idx) // 0 is passed in idx
// base case
if idx equals arr.length - 1
return true
// getting answer of the smaller problem
recursionResult = isArraySorted(arr, idx+1)
// self work
ans = recursionResult & arr[idx] <= arr[idx+1]
return ans