Paths in a Maze

Easy

0/40

18 upvotes

Asked in companies

Problem statement

You are given a 2-D matrix consisting of 0’s and 1’s with ‘N’ rows and ‘N’ columns, you are supposed to find all paths from the cell (0,0) (top-left cell) to the cell (N-1, N-1)(bottom-right cell). All cells with value 0 are blocked and cannot be travelled through while all cells with value 1 are open.

If you are currently at cell (x,y) then you can move to (x+1,y)(denoted by ‘D’), (x-1,y)(denoted by ‘U’), (x,y+1)(denoted by ‘R’), (x,y-1)(denoted by ‘L’) in one move. You cannot move out of the grid.

Example :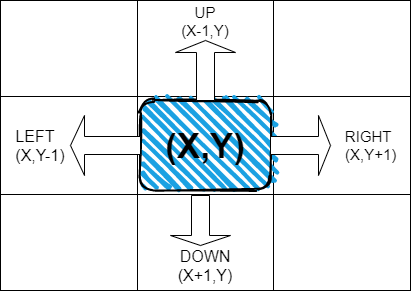

Detailed explanation ( Input/output format, Notes, Images )

Input Format :

The first line contains a single integer ‘T’ denoting the number of test cases. The test cases follow.

The first line of each test case contains a single integer ‘N’ denoting the number of rows and columns in the given matrix.

Next ‘N’ lines contain ‘N’ single space-separated integers each denoting the elements in the matrix.

Output Format :

For each test case, print all paths from (0,0) to (N-1, N-1) separated by a single space.

The output of every test case will be printed in a separate line.

Note :

You don’t need to print anything; It has already been taken care of.

Constraints :

1 <= T <= 5
1 <= N <= 5
0 <= ARR[i][j] <= 1

Where ‘T’ denotes the number of test cases, ‘N’ denotes the number of rows and columns of the given matrix, and ARR[i] denotes the value of the cell (i,j) in the given matrix.

Time Limit: 1 sec

Sample Input 1 :

Sample Output 1 :

DR RD
DR

Explanation of Sample Input 1 :

In the first test case, there are two paths from (0,0) to (1,1). The first path is (0,0)->(1,0)->(1,1) and the second path is (0,0)->(0,1)->(1,1)

In the second test case, there is only one path since the cell at (0,1) is blocked. The path is (0,0)->(1,0)->(1,1).

Sample Input 2 :

Sample Output 2 :

DDRR
DDRR RRDD

Explanation of Sample Input 2 :

In the first test case, there is only one path from (0,0) to (2,2). The path is (0,0)->(1,0)->(2,0)->(2,1)->(2,2).

In the second test case, there are two paths from (0,0) to (2,2). The first path is (0,0)->(1,0)->(2,0)->(2,1)->(2,2). and the second path is (0,0)->(0,1)->(0,2)->(1,2)->(2,2).

Console