Tries are a type of search tree, a tree data structure that is used to look for specific keys in a set of keys. In order to insert or access a key, we traverse in the depth-first order in the tree.
Introduction to tries
Suppose we want to implement a word-dictionary using a C++ program and perform the following functions:
Addition of the word(s)
Searching a word
Removal of the word(s)
To do the same, hashmaps can be thought of as an efficient data structure as the average case time complexity of insertion, deletion, and retrieval is O(1) .
Let us discuss the time complexity of the same in the case of strings.
Suppose we want to insert string abc in our hashmap. To do so, first, we would need to calculate the hashcode for it, which would require the traversal of the whole string abc. Hence, the time taken will be the length of the entire string irrespective of the time taken to perform any of the above operations. Thus, we can conclude that the insertion of a string will be O(string_length).
To search a word in the hashmap, we again have to calculate the hashcode of the string to be searched, and for that also, it would require O(string_length) time.
Similarly, for removing a word from the hashmap, we would have to calculate the hashcode for that string. It would again require O(string_length) time.
For the same purpose, we can use another data structure known as tries.
Below is the visual representation of the trie:
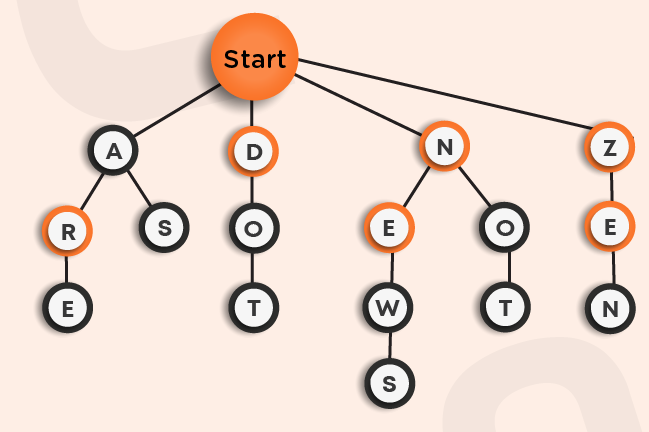
Here, the node at the top named as the start is the root node of our n-ary tree.
Suppose we want to insert the word ARE in the trie. We will begin from the root, search for the first letter A and then insert R as its child and similarly insert the letter E. You can see it as the left-most path in the above trie.
Now, we want to insert the word AS in the trie. We will follow the same procedure as above. First-of-all, we find the letter A as the child of the root node, and then we will search for S. If S was already present as the child of A, then we will do nothing as the given word is already present, otherwise, we will insert S. You can see this in the above trie. Similarly, we added other words in the trie.
This approach also takes O(word_length) time for insertion as everytime we explore through one of the branches of the Trie to check for the prefix of the word already present.
Moving on to searching a word in the trie, for that also, we would have to traverse the complete length of the string, which would take O(word_length) time.
Let us take an example. Suppose we want to search for the word DOT in the above trie, we will first-of-all search for the letter D as the direct child of the start node and then search for O and T and, then we will return true as the word is present in the trie.
Consider another example AR, which we want to search for in the given trie. Following the above approach, we would return true as the given word is present in it. However, ideally, we should return false as the actual word was ARE and not AR. To overcome this, it can be observed that in the above trie, some of the letters are marked with a bolder circle, and others are not. This boldness represents the termination of a word starting from the root node. Hence, while searching for a word, we will always be careful about the last letter that it should be bolded to represent the termination.
Note: While insertion in a trie, the last letter of the word should be bolded as a mark of termination of a word.
In the above trie, the following are all possibilities that can occur:
A, ARE, AS
DO, DOT
NEW, NEWS, NO, NOT
ZEN
Here, to remove the word, we will simply unbold the terminating letter as it will make that word invalid. For example: If you want to remove the string DO from the above trie by preserving the occurrence of string DOT, then we will reach O and then unbold it. This way the word DO is removed but at the same time, another word DOT which was on the same path as that of word DO was still preserved in the trie structure.
Similarly, if we want to remove DOT while keeping DO in the trie we traverse the trie and when we reach T we delete it. Now the child of O is deleted but O is still bolded because it is the end of the word of another key, so we don’t remove it from the trie and simply return from the function call.
For the removal of a word from trie, the time complexity is still O(word_length) as we are traversing the complete length of the word to reach the last letter to unbold it.
Given a word, we want to insert it into the Trie. We will assume that the word is already not present in the trie.
Steps for insert in the Trie
Start from the root.
For each character of the string, from first to the last, check if it has a child corresponding to itself in the root and if not exists create a new one.
Descend from the root to the child corresponding to the current character.
set the last character’s terminal property to be true.
function insert(root, word)
for each character c in word
/*
check if it already present and
if not then create a new node
*/
index = c - 'a'
if root.child[index] equals null
root.child[index] = new node
root = root.child[index]
// mark the last character to be the end of the word
root.isTerminal = true
return root
Search in Trie:
Given a word, we want to find out if it is present in the Trie or not.
Steps for search in the Trie
Start from the root.
For each character of the string, from first to the last check. if it has a child corresponding to itself in the root, and if not then return false.
Descend from the root to the child corresponding to the current character.
Return true on successful completion of the above loop if the last node is not null and its terminal property is true.
function search(root, word)
for each character c in word
/*
check if it already present and
if not then return false
*/
index = c - 'a'
if root.child[index] equals null
return false
root = root.child[index]
if root != null and root.isTerminal equals True
return true
else
return false
Delete in Trie:
Given a word, we want to remove it from the Trie if it is present.

Consider the above example. Suppose we want to remove NEWS from the trie. We recursively call the delete function and as soon as we reach S and mark its isTerminal property as false. Now we see that it has no children remaining so we delete it. After returning we get to W. We see that the condition: isTerminal is false and no children remaining, is false for this node hence we just simply return again. Proceeding the same way back up to E and N we delete the word NEWS from the trie.
Steps for delete in the Trie
Call the function delete for the root of the trie
Update the child corresponding to the current character by calling delete for the child.
If we have reached the final character, mark the isTerminal property of the node as False and delete this node if all the children are NULL for this node.
If all the children of this node have been deleted and this character is not the prefix of any other word we also delete the current node.
function delete(root, depth, word)
if root is null
/*
The word does not exist
hence return null
*/
return null
if depth == word.size
/*
mark the isTerminal as false and delete if no child is
present
*/
root.isTerminal = false
if root.children are null
delete(root)
root = null
return root
index = word[depth] - 'a'
/*
update the child of the root corresponding to the current
character
*/
root.children[index] = delete(root.children[index], depth + 1 , word)
if(root.children are null and root.isTerminal == false)
delete(root)
root = null
return root
if L is the length of the string we want to insert, search or delete from the trie, the time complexities of various operations are as follows: -

Problems related to Implementation of Tries
https://www.codingninjas.com/codestudio/problems/implement-trie_631356
https://www.codingninjas.com/codestudio/problems/trie-delete-operation_1062663
https://www.codingninjas.com/codestudio/problems/implement-a-phone-directory_1062666
Tries are used to implement data structures and algorithms like dictionaries, lookup tables, matching algorithms, etc.
They are also used for many practical applications like auto-complete in editors and mobile applications.
They are used in phone book search applications where efficient searching of a large number of records is required.
