Number of balanced binary trees

Easy

0/40

Average time to solve is 10m

18 upvotes

Asked in companies

Problem statement

You are given an integer ‘N’, you are supposed to find the number of balanced binary trees with height ‘N’. Since the answer can be very large, return the answer modulo 10^9+7.

Note :

A binary tree is considered balanced if the difference between the left subtree’s height and the right subtree’s height is less than or equal to 1, for all non-leaf nodes.

Example:

Consider N=2, there are three different binary trees.

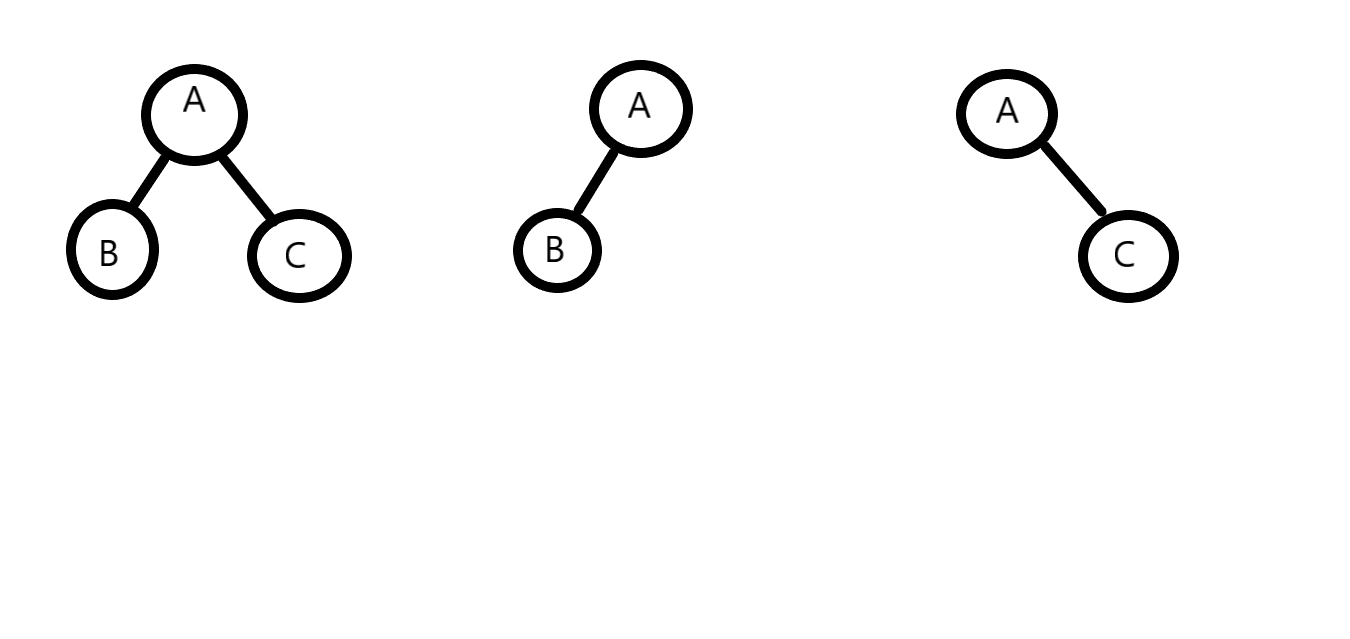
Detailed explanation ( Input/output format, Notes, Images )

Input Format :

The first line contains a single integer ‘T’ denoting the number of test cases. The test cases are as follows.

The first line of each test case contains a single integer ‘N’ denoting the height of the balanced binary tree.

Output Format :

For each test case, print the number of balanced binary trees with height ‘N’ modulo 10^9+7.

Print the output of each test case on a new line.

Note :

You don’t need to print anything; It has already been taken care of.

Constraints :

1 <= T <= 50
1 <= N <= 10 ^ 4

Where ‘T’ denotes the number of test cases, ‘N’ denotes the height of the balanced binary tree.

Time Limit: 1 sec

Sample Input 1 :

2
2
3

Sample Output 1 :

3
15

Explanation of Sample Input 1 :

In the first test case, the total number of binary trees with height 2 is 3.

In the second test case, the total number of binary trees with height 3 is 15.

Sample Input 2 :

1
4

Sample Output 2 :

Explanation of Sample Input 2 :

The total number of binary trees with height 4 is 315.

Console