Arrays

An array is defined as a fixed-size collection of elements of the same data type stored in contiguous memory locations. It is the simplest data structure where each element of the array can be accessed by using its index.

Properties of arrays

• Each element of the array is of the same data type and same size. For example: For an array of integers with the int data type, each element of the array will occupy 4 bytes.
• Elements of the array are stored in contiguous memory locations. For example :

200 is the starting address (base address) assigned to the first element of the array and each element of the array is of integer data type occupying 4 bytes in memory.

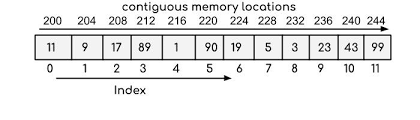
Accessing array elements

• The elements of the array are accessed by using their index. The index of an array of size N ranges from 0 to N-1.

For example: Accessing element at index 5: Array[5] -> this is the 6th element in the array.

• Every array is identified by its base address i.e the location of the first element of the array in memory. So, basically, the base address helps in identifying the address of all the elements of the array.
• Since the elements of an array are stored in contiguous memory locations, the address of any element can be accessed from the base address itself.

For example : 200 is the base address of the array, so address of element at index 4 will be 200 + 4 * (sizeof(int)) = 216.

Where can arrays be used?

• Arrays should be used where the number of elements to be stored is already known.
• Arrays are commonly used in computer programs to organize data so that a related set of values can be easily sorted or searched.
• Generally, when we require very fast access times, we usually prefer arrays since they provide O(1) access times.
• Arrays work well when we have to organize data in multidimensional format. We can declare arrays of as many dimensions as we want.
• If the index of the element to be modified is known beforehand, it can be efficiently modified using arrays due to quick access time and mutability.

Disadvantages of arrays

• Since arrays are fixed-size data structures you cannot dynamically alter their sizes. It creates a problem when the number of elements the array is going to store is not known beforehand.
• Insertion and Deletion in arrays are difficult and costly since the elements are stored in contiguous memory locations, hence, we need to shift the elements to create/delete space for elements.
• If more memory is allocated than required, it leads to the wastage of memory space and less allocation of memory also leads to a problem.

Time Complexity of various operations

• Accessing elements: Since elements in an array are stored at contiguous memory locations, they can be accessed very efficiently (random access) in O(1) time using indices.
• Inserting elements: Insertion of elements at the end of the array (at the index located to the right of the last element and there is still available space) takes O(1) time.

Insertion of elements at the beginning or at any index of the array involves moving elements to the right if there is available space. 

• If we want to insert an element at index i, all the elements starting from index i need to be shifted to the right by one position. Thus, the time complexity for inserting an element at index i is O(N - i).
• Inserting an element at the beginning of the array involves moving all elements by one position to their right, if there is available space, and takes O(N) time.
• Finding elements: Finding an element in an array takes O(N) time in the worst case, where N is the size of the array, as you may need to traverse the entire array.
• Deleting elements: Deletion of elements from the end of the array takes O(1) time.

Deleting elements from the beginning or at any index of the array involves moving elements to the left.

• If we want to delete an element at index i, all the elements starting from index (i + 1) need to be shifted to the left by one index. Thus, the time complexity for deleting an element at index i is O(N - i).
• Deleting an element from the beginning involves moving all elements starting from index 1 to left by one position, and takes O(N) time.