String Algorithms

In this section we will primarily talk about two string searching algorithms, Knuth Morris Pratt algorithm and Z - Algorithm.

Introduction

Suppose you are given a string text of length n and a string pattern of length m. You need to find all the occurrences of the pattern in the text or report that no such instance exists. 

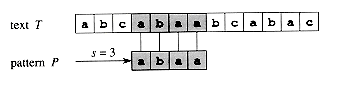
In the above example, the pattern “abaa” appears at position 3 (0 indexed) in the text “abcabaabcabac”. 

Naive Algorithm

A naive way to implement this pattern searching is to move from each position in the text and start matching the pattern from that position until we encounter a mismatch between the characters or say that the current position is a valid one.

In the given picture, The length of the text is 5 and the length of the pattern is 3. For each position from 0 to 3, we choose it as the starting position and then try to match the next 3 positions with the pattern. 

Naive pattern matching 

• For each i from 0 to N - M
• For each j from 0 to M - 1, try to match the jth character of the pattern with (i + j)th character of the string text.
• If a mismatch occurs, skip this instance and continue to the next iteration.
• Else output this position as a matching position.

Pseudocode:

function NaivePatternSearch(text, pattern)

    //   iterate for each candidate position 

    for i from 0 to text.length - pattern.length

        // boolean variable to check if any mismatch occurs    

        match  = True

        for j from 0 to pattern.length - 1

            //   if mismatch make match = False

            if text[i  + j] not equals pattern[j] 

                match = False

        //   if no mismatch print this position 

        if match == True

            print the occurrence  i 

    return 

Knuth Morris Pratt Algorithm 

We first define the prefix function of the string  - The prefix function of a string s is an array lps of length same as that of s such that lps[i] stores the information about the string s[0.. i]. It stores the length of the maximum prefix that is also the suffix of the substring s[0..i].

For example : 

For the pattern “AAAABAA”, 

lps[] is [0, 1, 2, 0, 1, 2, 3]

lps[0] is 0 by definition.  The longest prefix that is also the suffix of string s[0..1] which is AA is 1. (Note that we are only considering the proper prefix and suffix). Similarly, For the whole string AAABAAA it is 3, hence the lps[6] is 3. 

Algorithm for Computing the LPS array. 

• We compute the prefix values lps[i] in a loop by iterating from 1 to n - 1.
• To calculate the current value lps[i] we set the variable j denoting the length of best suffix for i - 1. So j = lps[i - 1].
• Test if the suffix of length j  + 1 is also a prefix by comparing s[j] with s[i]. If they are equal then we assign lps[i] = j  + 1 else reduce j = lps[j - 1].
• If we have reached j = 0 we assign lps[i] = 0  and continue to the next iteration .

Pseudocode:

function PrefixArray(s)

    n = s.length;

    //   initialize to all zeroes

    lps = array[n];

    for i from 1 to n - 1 

        j = lps[i-1];

        //   update j untill s[i] becomes equal to s[j]

        while j greater than 0 && s[i] no equal to s[j]

            j = lps[j-1];

        //   if extra character matches increase j 

        if s[i] equal to s[j]

            j += 1;

        //   update lps[i]

        lps[i] = j;

    //   return the array

    return lps

Algorithm for searching the pattern.

Now consider a new string S’ = pattern + ‘#’ + ‘text’ where + denotes the concatenation operator. 

Now, what is the condition that pattern appears at position [i - M + 1... i] in the string text. The lps[i] should be equal to M for the corresponding position of i in S’. Note that lps[i] cannot be larger than M because of the ‘#’ character.

• Create S’ = pattern + ‘#’ + ‘text’
• Compute the lps array of S’
• For each i from 2*M to M + N check the value of lps[i].
• If it is equal to M then we have found an occurrence at the position i - 2*M in the string text.

Pseudocode:

function StringSearchKMP(text, pattern)

    //   construct the new string 

    S' = pattern + '#' + text

    //   compute its prefix array

    lps = PrefixArray(S')

    N = text.length

    M = pattern.length

    for i from 2*M to M + N 

        //   longest prefix match is equal to the length of pattern

        if lps[i] == M

            //   print the corresponding position 

            print the occurrence i - 2*M 

    return 

Z - Algorithm

We first define the Z function of the string  - The Z function of a string S is an array Z of length same as that of S such that Z[i] denotes the length of the largest prefix that matches from the substring starting at position I.

For example : 

For the pattern “AAAABAA”, 

Z[] is [0, 3, 2, 1, 0, 2, 1]

Z[0] is 0 by definition.  The longest prefix that is also the prefix of string s[1..6] which is “AAABAA” is 3(This is equal to “AAA”). Similarly, For the whole string AAABAAA it is 1, hence the Z[6] is 1 since s[6.. 6] is ‘A’ and that is the longest possible prefix we can match.  

Algorithm for Computing the Z array. 

The idea is to maintain an interval [L, R] which is the interval with max R such that [L, R] is a prefix substring (substring which is also prefix). 

• if i > R, no larger prefix-substring is possible.
• Compute the new interval by comparing S[0] to S[i] i.e. string starting from index 0 i.e. from start with substring starting from index i and find z[i] using z[i] = R - L + 1.
• Else if, i ≤ R, [L, R] can be extended to i.
• For k = i - L, Z[i]  ≥  min( Z[k] , R - i + 1).
• If Z[k] < R - i + 1, no longer prefix substring s[i] exist.
• Else Z[k] ≥ R - i + 1, then there can be a longer substring.
• update [L, R] by changing L = i and changing R by matching from S[R+1]

Pseudocode:

function ZArray(s) 

    //   initialize to all zeroes

    Z = array[n];

    //   set the current window to the first character 

    l = 0

    r = 0

    for i from 1 to n - 1 

        //   first case i <= r

        if i <= r

            z[i] = min (r - i + 1, z[i - l]);

        //   increase prefix length while they are matching

        while i + z[i] < n and s[z[i]] == s[i + z[i]]

            z[i] += 1;

        //   update the window if i + z[i] crosses the window

        if i + z[i] - 1 > r

            l = i 

            r = i + z[i] - 1;

    //   return the array 

    return z

Algorithm for searching the pattern.

Now consider a new string S’ = pattern + ‘#’ + ‘text’ where + denotes the concatenation operator. 

Now, what is the condition that pattern appears at position [i. ...i + M - 1] in the string text. The Z[i] should be equal to M for the corresponding position of i in S’. Note that Z[i] cannot be larger than M because of the ‘#’ character. 

• Create S’ = pattern + ‘#’ + ‘text’
• Compute the lps array of S’
• For each i from M + 1 to N  + 1 check the value of lps[i].
• If it is equal to M then we have found an occurrence at the position i - M - 1 in the string text.

Pseudocode:

function StringSearchZ_Algo(text, pattern)

    //   construct the new string 

    S' = pattern + '#' + text

    //   compute its prefix array

    Z = ZArray(S')

    N = text.length

    M = pattern.length

    for i from M + 1 to  N + 1 

        //   longest prefix match is equal to the length of pattern

        if Z[i] == M

            //   print the corresponding position 

            print the occurrence i - M - 1

    return 

Time Complexities of string algorithms

Here ‘N’ is the total length of the pattern and ‘M’ is the length of the pattern we need to search.

Applications 

• Used in plagiarism detection between documents and spam filters.
• Used in bioinformatics and DNA sequencing to match DNA and RNA patterns
• Used in various editors and spell checkers to correct the spellings