Linked Lists
Introduction to linked lists
A linked list is a collection of nodes in non-contiguous memory locations where every node contains some data and a pointer to the next node of the same data type. In other words, the node stores the address of the next node in the sequence. A singly linked list allows traversal of data only in one way.
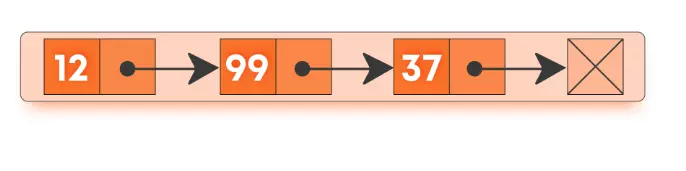
Following are the terms used in Linked Lists :
- Node: A node in a singly linked list contains two fields -
- Data field which stores the data at the node
- A pointer that contains the address of the next node in the sequence.
- Head: The first node in a linked list is called the head. The head is always used as a reference to traverse the list.
- Tail: The last node in a linked list is called the tail. It always contains a pointer to NULL (since the next node is NULL), denoting the end of a linked list.
Properties of Linked Lists
- A linked list is a dynamic data structure, which means the list can grow or shrink easily as the nodes are stored in memory in a non-contiguous fashion.
- The size of a linked list is limited to the size of memory, and the size need not be declared in advance.
- Note: We must never lose the address of the head pointer as it references the starting address of the linked list and if lost, would lead to loss of the list.
Types of Linked Lists
There are generally three types of linked list:
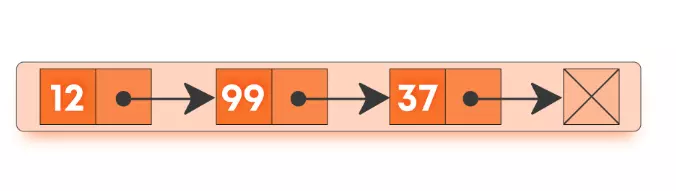
- Singly: Each node contains only one link which points to the subsequent node in the list.
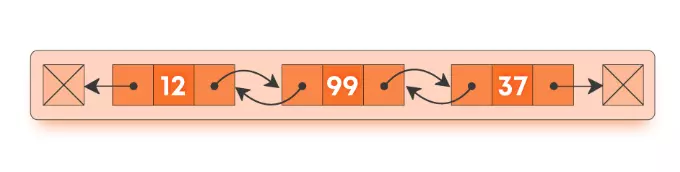
- Doubly: It’s a two-way linked list as each node points not only to the next pointer but also to the previous pointer.
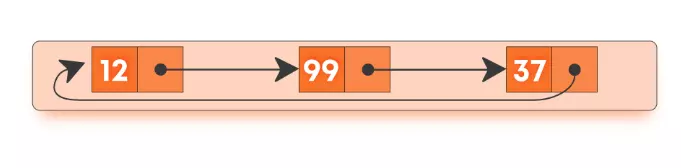
- Circular: There is no tail node i.e., the next field is never NULL in any node, and the next field for the last node points to the head node.
Singly Linked Lists
Operations on Singly Linked Lists
INSERTION OPERATION
- Insertion at beginning
function insertAtBeginning(data)
/*
create a new node : newNode
set newNode’s data to data
*/
newNode.data = data
// If the list is empty, set head as newNode
if head is null
head = newNode
return head
/*
Otherwise set newNode as new head after setting its next
pointer to current head.
*/
newNode.next = head
head = newNode
return head- Insertion at end
function insertAtEnd(data)
/*
create a new node : newNode
set newNode’s data to data
*/
newNode.data = data
// If the list is empty, set head as newNode
if head is null
head = newNode
return head
/*
Otherwise, create a cur node pointer and keep moving it
until it reaches the last node
*/
cur = head
while cur.next is not null
cur = cur.next
/*
Now cur points to the last node of the linked list; set the
next pointer of this node to the newNode
*/
cur.next = newNode
return head- Insertion at a given index ( idx will be 0 indexed )
function insertAtIdx(idx, data)
/*
create a new node : newNode
set newNode’s data to data
*/
newNode.data = data
if (idx == 0)
// Case of insertion at beginning
insertAtBeginning(data)
else
/*
Moving the cur node pointer till the given index and
maintaining a prev node where the node is to be
inserted
*/
count = 0
cur = head
while count < idx - 1 and cur.next is not null
count += 1
cur = cur.next
/*
If count does not reach (idx - 1), then the given index
is greater than the size of the list
*/
if count < idx - 1
print “invalid index”
return head
/*
Otherwise setting the newNode next field as the
address of the node present at position idx
*/
newNode.next = cur.next
/*
Updating the cur node next field as the address of
the newNode
*/
cur.next = newNode
return head
DELETION OPERATION
- Deletion from beginning
function deleteFromBeginning()
// If the list is empty, return null
if head is null
print “Linked List is empty”
return null
/*
Otherwise set the new head to the node whose
address is stored in the current head.
*/
temp = head
head = head.next
delete temp
return head- Deletion from end
function deleteFromEnd()
// If the list is empty, return null
if head is null
print “Linked List is empty”
return null
// Otherwise, check if the list contains a single node
if head.next is null
temp = head
head = head.next
delete head
return head
/*
Otherwise, create a cur and prev node pointer and keep moving cur until it reaches the last node
of the list
*/
cur = head.next
prev = head
while cur.next is not null
prev = cur
cur = cur.next
/*
Now cur points to the last node of the linked list and prev to the node behind it; set the next
pointer of prev node null.
*/
prev.next = null
delete cur
return head- Deletion from the given index ( idx will be 0 indexed )
function deleteFromIdx(idx)
if (idx == 0)
// Case of deletion from beginning
deleteFromBeginning()
else
count = 0
cur = head
/*
Moving the cur node pointer until count is less than the index-1 from where the node is
to be deleted
*/
while count < idx - 1 and cur is not null
count += 1
cur = cur.next
/*
If the cur node reaches null or the tail of the list, then the given index is greater than the
size of the list
*/
if cur is null or cur.next is null
print “invalid index”
return null
/*
Otherwise updating the next field of cur node to be the address of the node present in the
next field of the node to be deleted
*/
nextNode = cur.next
cur.next = nextNode.next
delete nextNode
return headSEARCH OPERATION
function search(data)
// Create a cur node pointer initialized to head of the linked list
cur = head
/*
Traverse the linked list, and compare the data of cur and the data to be searched
*/
while cur is not null
if cur.data equals data
return true
cur = cur.next
// If data is not found, return false
return falseDISPLAY OPERATION
function display()
// Create a cur node pointer initialized to head of the linked list
cur = head
/*
Traverse the linked list and print the data of the element represented by the cur pointer
*/
while cur is not null
print cur.data
cur = cur.next
Time Complexity of various operations
Let ‘n’ be the number of nodes in the linked list. The time complexities of linked list operations in the worst case can be given as:

Applications of Linked Lists
- Linked Lists can be used to implement useful data structures like stacks and queues.
- Linked Lists can be used to implement hash tables, each bucket of the hash table can be a linked list.
- Linked Lists can be used to implement graphs (Adjacency List representation of graph).
- Linked Lists can be used in a refined way in implementing different file systems in one form or another.
Advantages of Linked Lists
- It is a dynamic data structure, which can grow or shrink according to the requirements.
- Insertion and deletion of elements can be done easily and does not require movement of all elements when compared to arrays.
- Allocation and deallocation of memory can be done easily during execution.
- Insertion at the beginning is a constant time operation and takes O(1) time, as compared to arrays where inserting an element at the beginning takes O(n) time, where n is the number of elements in the array.
Disadvantages of Linked Lists
- Linked lists consume more memory as compared to arrays.
- As the elements in a linked list are not stored in a contiguous fashion in memory, so require more time to access the elements as compared to arrays.
- Appending an element to a linked list is a costly operation, and takes O(n) time, where n is the number of elements in the linked list, as compared to arrays that take O(1) time.
Doubly Linked Lists
Why doubly linked lists?
Doubly Linked Lists contain an extra pointer pointing towards the previous node (called the previous pointer) in addition to the pointer pointing to the next node (called the next pointer).
The advantage of using doubly linked lists is that we can navigate in both directions.
A node in a singly linked list can not be removed unless we have the predecessor node. But in a doubly-linked list, we don’t need access to the predecessor node.

Operations on doubly linked lists
Insertion Operations
- insertAtBeginning(data): Inserting a node in front of the head of a linked list.
- insertAtEnd(data): Inserting a node at the tail of a linked list.
- insertAtIdx(idx, data): Inserting a node at a given index.
Deletion Operations
- deleteFromBeginning: Deleting a node from the front of a linked list.
- deleteFromEnd: Deleting a node from the end of a linked list.
- deleteFromIdx(idx): Deleting a node at a given index.
Implementation of doubly LinkedList
Doubly Linked Lists contain a head pointer that points to the first node in the list ( head is null of the list is empty ).
Each node in a doubly-linked list has three properties: data, previous(pointer to the previous node), next(pointer to the next node).
- Insert at beginning
function insertAtBeginning(data)
/*
create a new node : newNode
set newNode’s data to data
*/
newNode.data = data
// If list is empty, set head as newNode
if head is null
head = newNode
return head
newNode.next = head
head.previous = newNode
head = newNode
return head- Insert at end
function insertAtEnd(data)
/*
create a new node : newNode
set newNode’s data to data
*/
newNode.data = data
// If list is empty, set head as newNode
if head is null
head = newNode
return head
/*
Otherwise, create a cur node pointer and keep moving it
until it reaches the last node of the list
*/
cur = head
while cur.next is not null
cur = cur.next
/*
Now cur points to the last node of the linked list; set the next
pointer of this node to the newNode
*/
cur.next = newNode
newNode.previous = cur
return head- Insert at given index ( idx will be 0 indexed )
function insertAtGivenIdx(idx, data)
/*
create a new node : newNode
set newNode’s data to data
*/
newNode.data = data
// call insertAtBeginning if idx = 0
if idx == 0
insertAtBeginning(data)
return head
count = 0
cur = head
while count < idx - 1 and cur.next is not null
count += 1
cur = cur.next
/*
If count does not reach (idx - 1), then the given index
is greater than the size of the list
*/
if count < idx - 1
print “invalid index”
return head
/*
Otherwise setting the newNode next field as the address of the node present at position idx
*/
nextNode = cur.next
cur.next = newNode
newNode.prev = cur
if nextNode is not null
nextNode.prev = newNode
newNode.next = nextNode
return head- Delete from beginning
function deleteFromBeginning()
// if the head is null, return
if the head is null
print “Linked List is Empty”
return head
temp = head
head = head.next
head.prev = null
delete temp
return head- Delete from end.
function deleteFromEnd()
// list is empty if the head is null
if the head is null
print “list is Empty”
return head
/*
Keep a cur pointer and let it point to the head; move the cur
pointer till cur.next is not equal to null
*/
cur = head
while cur.next is not equal to null
cur = cur.next
prevNode = cur.prev
prevNode.next = null
delete cur
return head- Delete from given index ( idx will be 0 indexed )
function deleteFromGivenIdx(idx)
// call deleteFromBeginning if idx = 0
if idx == 0
deleteFromBeginning()
return head
count = 0
temp = head
while count < idx - 1 and temp is not equal to null
count++
temp = temp.next
if temp = null or temp.next is equal to null
print “Invalid Index”
return head
nextNode = temp.next
prevNode = temp.prev
prevNode.next = nextNode
nextNode.previous = prevNode
delete temp
return head
Time Complexity of various operations
Let ‘n’ be the number of elements in the linked lists. The complexities of linked list operations with this representation can be given as:

Advantages of Doubly Linked Lists
- Doubly Linked Lists can be traversed in both directions.
- Deletion is easy in doubly linked lists if we know the address of the node to be deleted whereas in singly-linked lists we need to traverse the list to get the previous node.
- Reversing a doubly linked list is easier.
Disadvantages of Doubly Linked Lists
- We need to maintain an extra pointer for each node.
- Every operation in doubly linked lists requires updating of an extra pointer.
Applications of Doubly Linked Lists
- It is used by web browsers for backward and forward navigation of web pages
- LRU ( Least Recently Used ) / MRU ( Most Recently Used ) Cache is constructed using Doubly Linked Lists.
- Used by various applications to maintain undo and redo functionalities.
- In Operating Systems, a doubly-linked list is maintained by the thread scheduler to keep track of processes that are being executed at that time.
Circular Linked Lists
What are circular linked lists?
Circular linked lists are just linked lists where the next pointer of the last node is pointing to the first node of the list. There is no head node.
Why circular linked lists?
The advantage of using a circular linked list is that when we want to traverse in only one direction and move to the first node cyclically, we don’t need to store additional pointers to mark the first and the last node. Typical usage of this concept is to implement queues using one pointer.
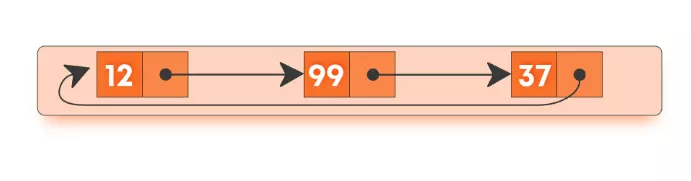
Operations on circular linked lists
- insertAtBeginning(data): Inserting a node in front of the head of a linked list.
- deleteFromBeginning: Deleting a node from the front of a linked list.
- display: Display the contents of the linked list
Implementation of circular linked list
Circular Linked Lists will have one pointer: head
Each node in a circular-linked list has two properties: data, next(pointer to the next node).
- Insert at beginning
function insertAtBeginning(data)
/*
create a new node : newNode
set newNode’s data to data
*/
newNode.data = data
// If list is empty, set head as newNode
if head is null
head = newNode
head.next = head
return head
// traverse to the end of the circular list
temp = head
while temp.next != head
temp = temp.next
// set the next of temp as newNode and return head
newNode.next = head
temp.next = newNode
head = newNode
return head- Delete from beginning
function deleteFromBeginning()
// if the head is null, return
if head is null
print “Linked List is Empty”
return head
if head.next == head
head = NULL
return head
// traverse to the end of the circular list
temp = head
while temp.next != head
temp = temp.next
// set the next of temp as next of head
temp.next = head.next
delete head
head = temp.next
return head- Display
function display()
/*
create a new node : newNode
set newNode’s data to data
*/
// If the list is empty, print nothing
if the head is null
print “list empty”
return
// traverse to the end of the circular list until the head is encountered
temp = head
while temp.next != head
print (temp.data)
temp = temp.next
print(temp.data)
return
Time Complexity of various operations
Let ‘n’ be the number of elements in the linked lists. The complexities of linked list operations with this representation can be given as:

Advantages of Circular Linked Lists
- We can start traversing the list from any node. We just have to keep track of the first visited node.
- They make the implementation of data structures like queues a lot easier and more space-efficient as compared to singly-linked lists.
- They can perform all the functionalities supported by singly-linked lists in addition to their own advantages.
Disadvantages of Circular Linked Lists
- Operations like insertion and deletion from the beginning become very expensive as compared to singly-linked lists.
- We need to maintain an extra pointer that marks the beginning of the list to prevent getting into an infinite loop.
Applications of Circular Linked Lists
- They are used for implementations of data structures like Fibonacci heap where a circular doubly linked list is used.
- They can be used to implement circular queues that have applications in CPU scheduling algorithms like round-robin scheduling.
- They are used to switch between players in multiplayer games.