Introduction to stacks

• Stacks are simple data structures that allow us to store and retrieve data sequentially.
• A stack is a linear data structure like arrays and linked lists.
• It is an abstract data type (ADT).
• In a stack, the order in which the data arrives is essential. It follows the LIFO order of data insertion/abstraction. LIFO stands for Last In First Out.
• Consider the example of a pile of books:

Here, unless the book at the topmost position is removed from the pile, we can’t have access to the second book from the top and similarly, the books below the second one. When we apply the same technique to the data in our program then, this pile-type structure is said to be a stack. 

Like deletion/removal, we can only insert the book at the top of the pile rather than at any other position. This means that the object/data that made its entry at the last would be one to come out first, hence known as LIFO. 

Various operations on stacks

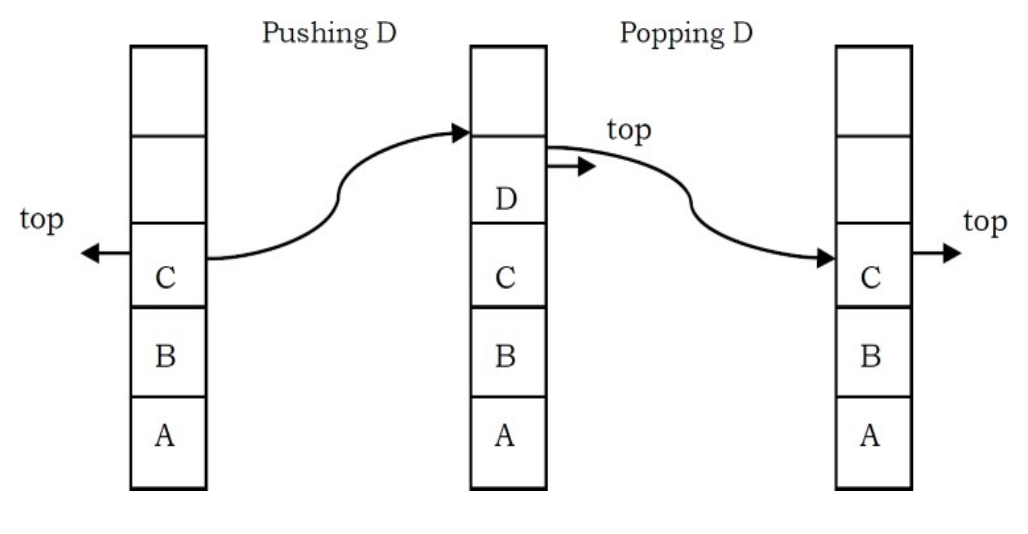
In a stack, insertion and deletion are done at one end, called top.

• Insertion: This is known as a push operation.
• Deletion: This is known as a pop operation.

Main stack operations

• push (data): Insert data onto the stack.

• pop(): Removes and returns the last inserted element from the stack.

Auxiliary stack operations

• top(): Returns the last inserted element without removing it.

• int size(): Returns the number of elements stored in the stack.

• boolean isEmpty(): Indicates whether any elements are stored in the stack or not i.e. whether the stack is empty or not.

Implementation of Stacks

Stacks can be implemented using arrays, linked lists, or queues. The underlying algorithm for implementing operations of the stack remains the same.

• Push operation

function push(data, stack)
    //   data : the data to be inserted into the stack.
    if stack is full
        return null
    /*
        top : It refers to the position (index in arrays) of the last 
        element into the stack
    */
    top = top + 1
    stack[top] = data

• Pop operation

function pop(stack)
    if stack is empty
        return null

    //   Retrieving data of the element to be popped.
    data = stack[top]
    //   Decrementing top 
    top = top - 1
    return data

• Top operation

function top(stack)
    if stack is empty
        return null
    else
        return stack[top]

• isEmpty operation

function isEmpty(stack)
    if top is null 
        return true
    else
        return false

Time Complexity of various operations

Let ‘n’ be the number of elements in the stack. The complexities of stack operations with this representation can be given as:

Exceptions

• Attempting the execution of an operation may sometimes cause an error condition, called an exception.
• Exceptions are said to be “thrown” by an operation that cannot be executed.
• Attempting the execution of pop() on an empty stack throws an exception called Stack Underflow.
• Trying to push an element in a full-stack throws an exception called Stack Overflow.

Applications of stacks

• Stacks are useful when we need dynamic addition and deletion of elements in our data structure. Since stacks require O(1) time complexity for all the operations, we can achieve our tasks very efficiently.
• It also has applications in various popular algorithmic problems like:-
  • Tower of Hanoi
  • Balancing Parenthesis
  • Infix to postfix
  • Backtracking problems
• It is useful in many Graph Algorithms like topological sorting and finding strongly connected components.
• Apart from all these it also has very practical applications like:
  • Undo and Redo operations in editors
  • Forward and backward buttons in browsers
  • Allocation of memory by an operating system while executing a proces

Introduction to queues

• Queues are simple data structures in which insertions are done at one end and deletions are done at the other end.
• It is a linear data structure as arrays.
• It is an abstract data type (ADT).
• The first element to be inserted is the first element to be deleted. It follows either FIFO (First in First Out) or LILO (Last In Last Out).
• Consider the queue as the line of people.

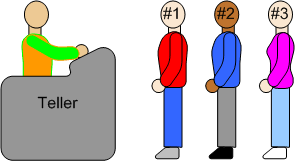
The above picture shows that when we enter the queue/line, we stand at the end of the line and the person who is at the front of the line is the one who will be served first.

After the first person is served, he will exit, and as a result, the next person will come at the head of the line. Similarly, the head of the queue will keep exiting the line as we move towards the front/head of the line. Finally, we reach the front. we are served and we exit. This behavior is useful when we need to maintain the order of arrival.

Various operations on queues

In queues, insertion is done at one end (rear) and deletion is done at other end (front) :

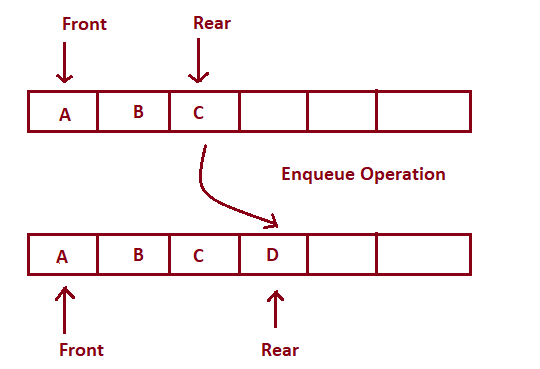
Enqueue Operation

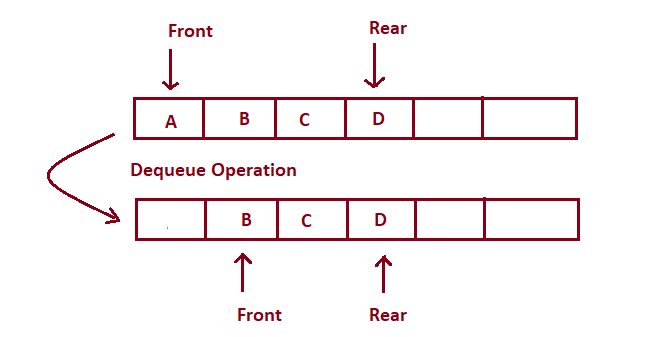
Dequeue Operation

• Insertion: Adding elements at the rear side. The concept of inserting an element into the queue is called Enqueue. Enqueueing an element, when the queue is full, is called overflow.
• Deletion: Deleting elements at the front side. The concept of deleting an element from the queue is called Dequeue. Deleting an element from the queue when the queue is empty is called underflow.

Main Queue Operations:

• enqueue(data) : Insert data in the queue (at rear).
• dequeue() : Deletes and returns the first element of the queue (at front).

Auxiliary Queue Operations:

• front() : returns the first element of the queue.
• int size() : returns number of elements in the queue.
• boolean isEmpty() : returns whether the queue is empty or not.

How can queues be implemented?

Queues can be implemented using arrays, linked lists or stacks. The basic algorithm for implementing a queue remains the same.

We will use array-based implementation here. We maintain two variables for all the operations: front, rear.

• Enqueue Operation

function enqueue(data)                     
    if queue is full
        return “Full Queue Exception”
        
    queue[rear] = data 
    rear++

• Dequeue Operation

function  dequeue()
    if queue is empty
        return “Empty Queue Exception”
           
    temp = queue[front]  
    front++
    return temp    

• getFront() Operation

function getFront()
    if queue is empty
        return “Empty Queue Exception”
    temp = queue[front]
    return temp      

Time Complexity of various operations

Let ‘n’ be the number of elements in the queue. The complexities of queue operations with this representation can be given as:

Applications of queues

Real-Life Applications

• Scheduling of jobs in the order of arrival by the operating system
• Multiprogramming
• Waiting time of customers at call centers
• Asynchronous data transfer

Application in solving DSA problems 

• Queues are useful when we need dynamic addition and deletion of elements in our data structure. Since queues require O(1) time complexity for all the operations, we can achieve our tasks very efficiently.
• It is useful in many Graph Algorithms like breadth-first search, Dijkstra’s algorithm, and prim’s algorithm.