Trees
Introduction to Trees
A tree is a data structure similar to linked lists but instead of each node pointing to just one next node in a linear fashion, each node points to a number of nodes. The tree is a non-linear data structure. A tree structure is a way of representing a hierarchical nature of a structure in a graphical form.
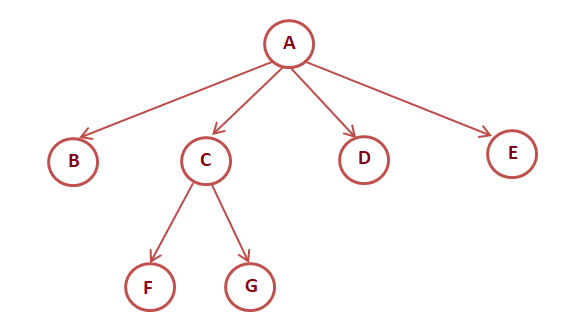
Properties of Trees
- Root: The root of the tree is the node with no parents. There can be at most one root node in the tree (Eg: A is the root node in the above example).
- Parent: For a given node, its immediate predecessor is known as its parent node. In other words, nodes having 1 or more children are parent nodes. (Eg: A is the parent node of B, C, D, E, and C is the parent node of F, G)
- Edge: An edge refers to the link from the parent node to the child node.
- Leaf: Nodes with no children are called leaf nodes (Eg: B, F, G, D, E are leaf nodes in the above example).
- Siblings: Children with the same parent are called siblings. (Eg: B, C, D, E are siblings, and F, G are siblings).
- A node x is an ancestor of node y if there exists a path from the root to node y such that x appears on the path. Node y is called the descendant of node x. (Eg: A is an ancestor of node F, G)
- Depth: The depth of a node in the tree is the length of the path from the root to the node. The depth of the tree is the maximum depth among all the nodes in the tree.
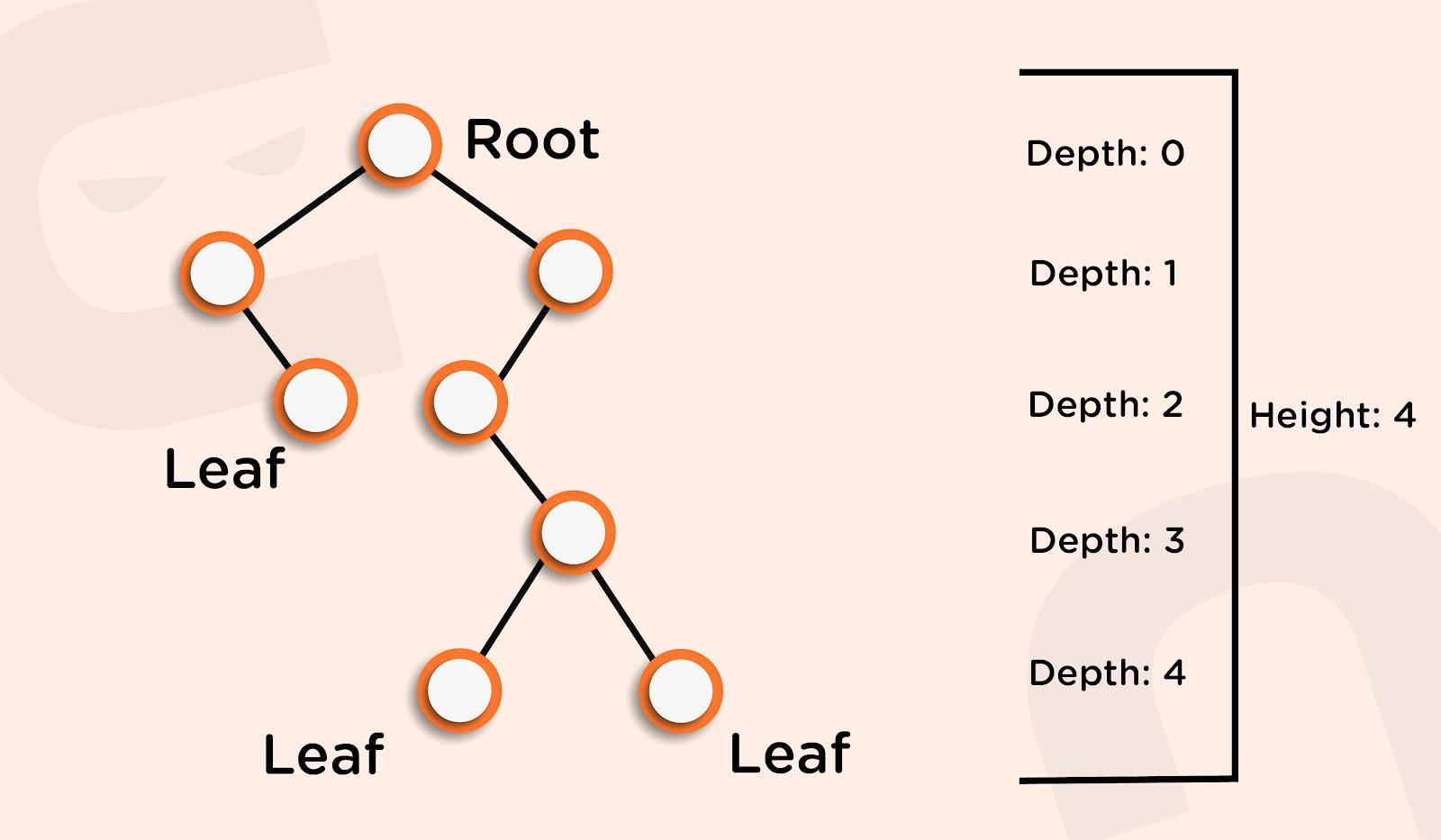
- Height: The height of the node is the length of the path from that node to the deepest node in the tree. The height of the tree is the length of the path from the root node to the deepest node in the tree. (Eg: the height of the tree in the above example is four (count the edges, not the nodes)).
- A tree with only one node has zero height.
- For a given tree, depth and height returns the same value but may be different for individual nodes.
- Skew Trees: If every node in a tree has only one child then we call such a tree a skew tree. If every node has only a left child, we call them left skew trees. If every node has only the right child, we call them right skew trees.
Binary Trees
A tree is called a binary tree if every node in the tree has either zero, one, or two children. An empty binary tree is also a valid binary tree. A binary tree is made of nodes that constitute a left pointer, a right pointer, and a data element. The root pointer is the topmost node in the tree.
We can visualize a binary tree as the root node and two disjoint binary trees, called the left subtree and the right subtree.
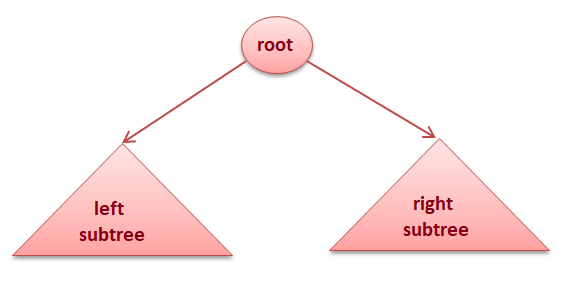
Types of Binary Trees
- Strict Binary Tree: A binary tree in which each node has exactly zero or two children.
- Full Binary Tree: A binary tree in which each node has exactly two children and all the leaf nodes are at the same level.
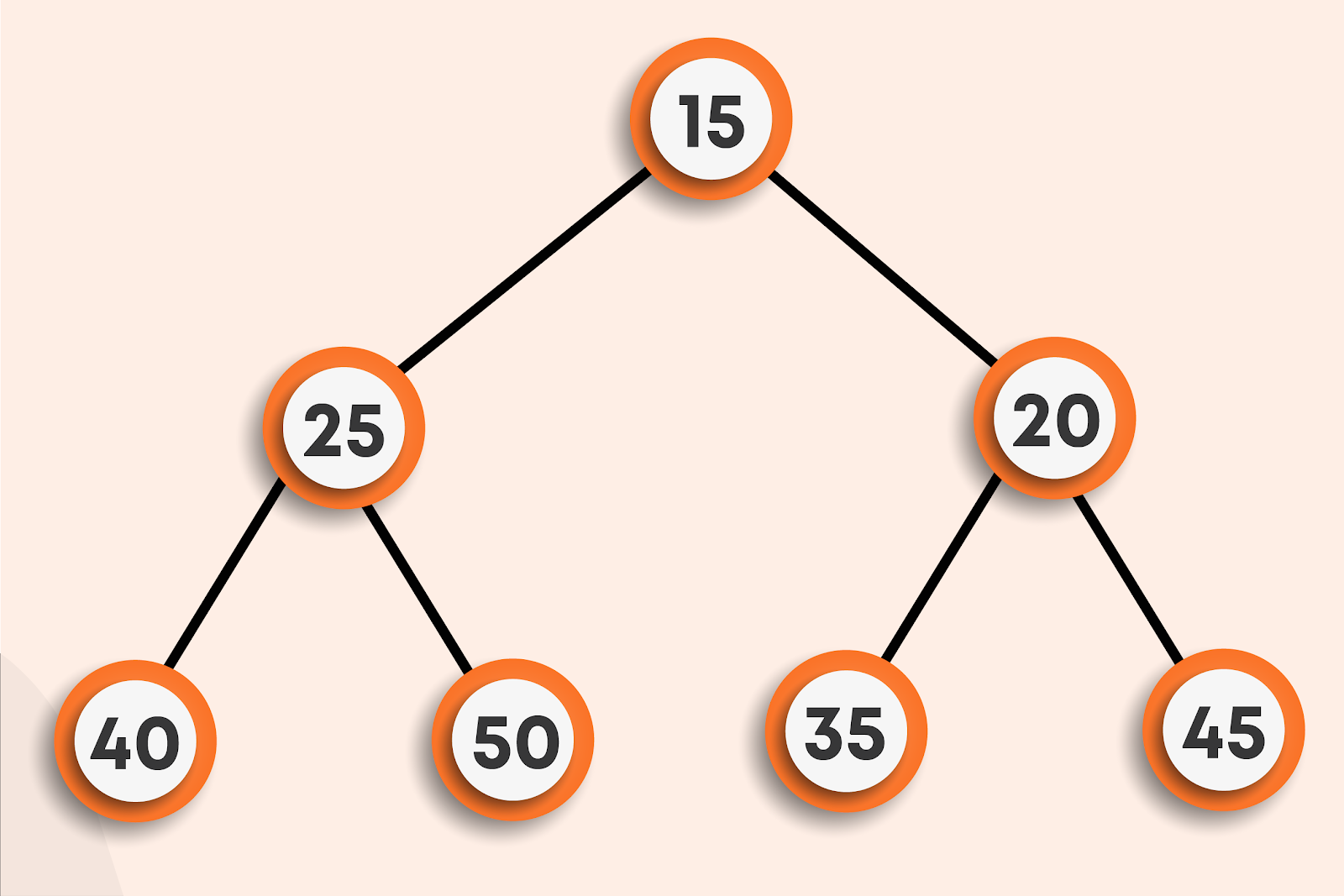
- Complete Binary Tree: A complete binary tree has all the levels filled except for the last level, which has all its nodes as much as to the left.
- A degenerate tree: In a degenerate tree, each internal node has only one child.
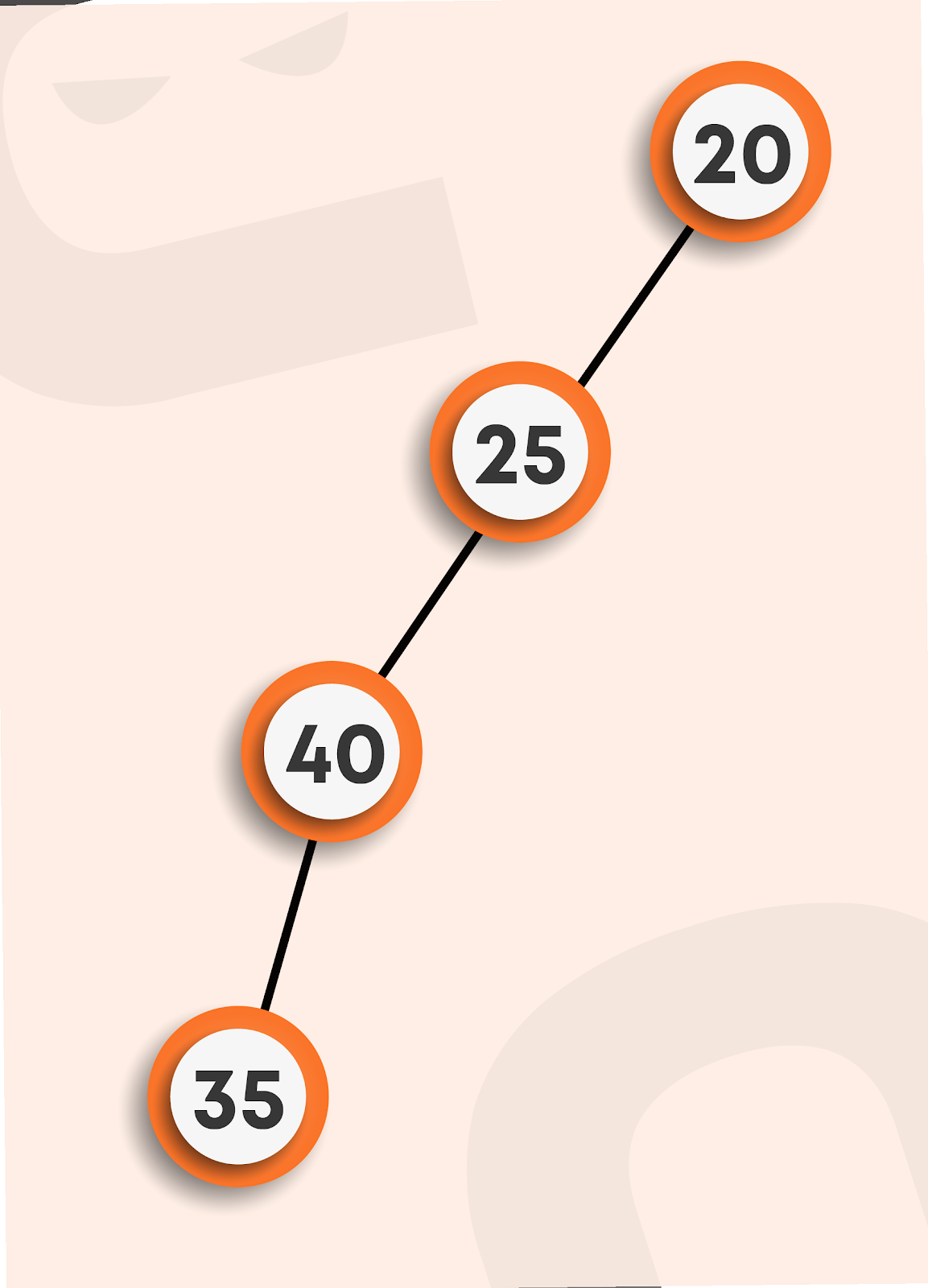
Properties of a Binary Tree
For the given properties, let’s assume that the tree has a height of h, also the root node is at a height of 0.
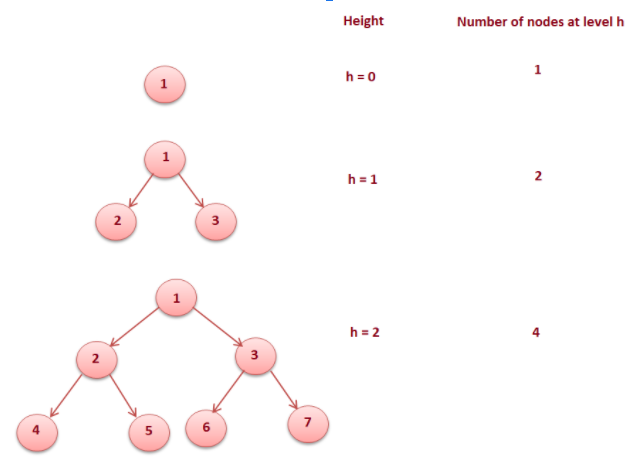
From the diagram, we can say that
- The number of nodes in a full binary tree is 2^(h+1) -1
- The number of leaf nodes in a full binary tree is 2^h
- The number of node links in a complete binary tree of n nodes is n + 1 .
Structure of Binary trees

Each node in a binary tree contains data, a left pointer, and a right pointer.
Binary tree traversals
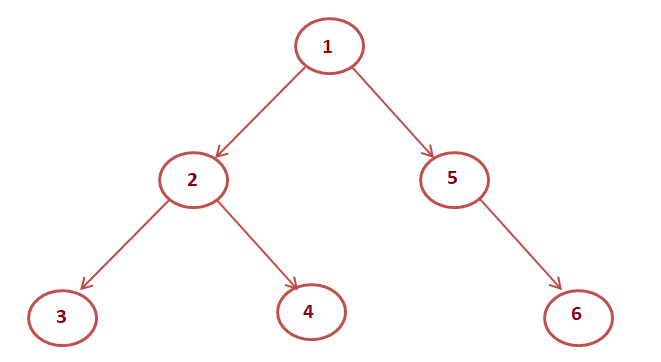
The process of visiting all the nodes of the tree is called tree traversal. Each node is processed only once but may be visited more than once. We will be considering the below tree for all the traversals.
D: Current node
L: Left Subtree
R: Right Subtree
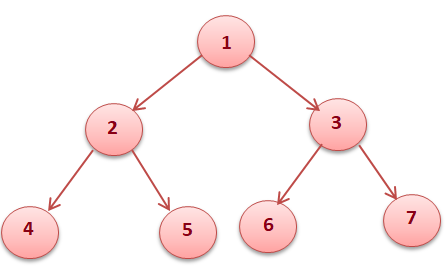
- PreOrder Traversal (DLR)
In preorder traversal, each node is processed before processing its subtrees.
Like in the above example, 1 is processed first, then the left subtree, and this is followed by the right subtree. Therefore processing must return to the right subtree after finishing the processing of the left subtree. To move to the right subtree after processing the left subtree we have to maintain the root information.
Steps for preOrder traversal
- Visit the root.
- Traverse the left subtree in Preorder.
- Traverse the right subtree in Preorder.
function preOrderTraversal(root)
if root is null
return
// process current node
print “root.data”
// calling function recursively for left and right subtrees
preOrderTraversal(root.left)
preOrderTraversal(root.right)
PreOrder Output of above tree : 1 2 4 5 3 6 7
- InOrder Traversal (LRD)
In inorder traversal, the root is visited between the subtrees.
Steps for InOrderTraversal
- Traverse the left subtree in Inorder.
- Visit the root.
- Traverse the right subtree in Inorder.
function inOrderTraversal(root)
if root is null
return
// calling function recursively for left subtree
inOrderTraversal(root.left)
// process current node
print “root.data”
// calling function recursively for right subtree
inOrderTraversal(root.right)
InOrder Output of above tree : 4 2 5 1 6 3 7
- PostOrder Traversal(LDR)
In postorder traversal, the root is visited after the left and right subtrees respectively.
Steps for postOrder traversal
- Traverse the left subtree in postOrder.
- Traverse the right subtree in postOrder.
- Visit the root.
function postOrderTraversal(root)
if root is null
return
// calling function recursively for left and right subtrees
postOrderTraversal(root.left)
postOrderTraversal(root.right)
// process current node
print “root.data”
postOrder output of above tree : 4 5 2 6 7 3 1
- LevelOrder Traversal
In level order traversal, each node is visited level-wise in increasing order of levels from left to right.
Steps for levelOrder traversal
- Visit the root.
- While traversing the level l, add all the elements at (l + 1) in the queue
- Go to the next level and visit all the nodes at that level.
- Repeat this until all levels are completed.
function levelOrderTraversal()
if root is null
return
// Create queue of type Node and add root to the queue
queue.add(root).
while the queue is not empty
// remove the front item from the queue
removedNode= queue.remove()
// process the removedNode
print “removeNode.data”
/*
Add the left and right child of the removedNode if they are not null
*/
if removedNode.left is not null
queue.add(removedNode.left)
if removedNode.right is not null
queue.add(removedNode.right)
end
LevelOrder output of above tree: 1 2 3 4 5 6 7
Operations on a binary tree
- Count nodes in a binary tree.
- Find the maximum value in a binary tree.
- Search a value in a binary tree.
- Height of a binary tree.
Count nodes in a binary tree.
function countNodesInABinaryTree(root)
if the root is null
return 0
/*
Count nodes in the left subtree and right subtree recursively
and add 1 for self node
*/
leftCount = countNodesInABinaryTree(root.left)
rightCount = countNodesInABinaryTree(root.right)
return leftCount + rightCount + 1
Find maximum value in a binary tree.
function findMax(root)
if root is null
return Integer.MIN_VALUE
/*
Find Maximum in the left subtree and right subtree recursively
and compare self data, max of left subtree, max of right
subtree and return max of these three
*/
max = root.data
leftMax = findMax(root.left)
rightMax = findMax(root.right)
if leftMax > max
max = leftMax
if rightMax > max
max = rightMax
return max
Search a value in a binary tree.
function search(root, val)
if the root is null
return false
/*
If the current node’s data is equal to val then return true
Else call the function for left and right subtree.
*/
if root.data equals val
return true
return search(root.left, val) || search(root.right, val)
Height of a binary tree.
function findHeight(root)
if root is null
return 0
/*
Find the height of the left subtree and right subtree.
Then add 1 (for current node) to max value from leftHeight
and rightHeight
*/
leftHeight = findHeight(root.left)
rightHeight = findHeight(root.right)
return 1 + max(leftHeight, rightHeight)
Time Complexity

Generic Trees (N-ary Trees)
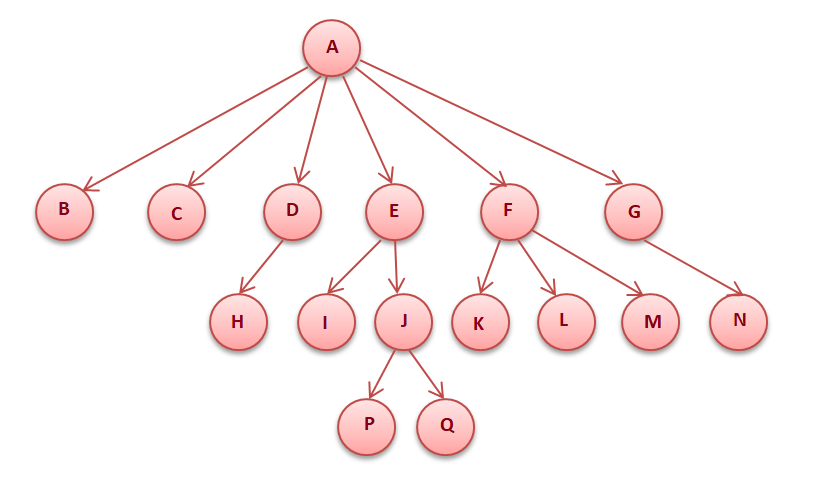
The generic tree is a collection of nodes in which node has at most N children. A generic tree consists of a list of pointers to the child nodes and the data element. The root pointer is the topmost node in the tree.
Printing a generic tree (recursively)

function printTree(root)
// process current node
print “root.data”
// calling function recursively for childNodes
for every childNode in the root.children list
printTree(childNode)
The output of the above tree: A B C D H E I J P Q F K L M G N
LevelOrder Printing of Generic Tree
Steps for levelOrder traversal
- Visit the root.
- While traversing the level l, add all the elements at (l + 1) in the queue.
- Go to the next level and visit all the nodes at that level.
- Repeat this until all levels are completed.
function levelOrderTraversal()
If the root is null
return
// Create queue of type Node and add root to the queue
queue.add(root)
while the queue is not empty
// remove the front item from the queue
removedNode= queue.remove()
print “removedNode.data”
/*
Add the childNodes of the removedNode to the queue
*/
for every childNode in removedNode.children list
queue.add(childNode)
end
LevelOrder output of above tree: A B C D E F G H I J K L M N P Q
Application of trees
- Expression trees are used in compilers
- Huffman coding trees are used in data compression algorithms.
- Used to implement indexing in databases through B- Tree and B+ Tree.
- Used to implement dictionaries(tries) for lookup.