Priority Queues & Heaps Notes

Note

Priority Queues & Heaps

Introduction

A priority queue ADT is a data structure that supports the operation Insert and DeleteMin (which returns and removes the minimum element) or DeleteMax (which returns and deletes the max element).

A priority queue is called an ascending - priority queue, if the item with the smallest key has the highest priority (means delete the smallest element always). Similarly, a priority queue is called descending - priority queue if the item with the largest key has a greater priority (delete the maximum priority always). Since the two operations are symmetric we will be discussing ascending priority queues.

Difference between Priority Queue and Normal Queue

In a queue, the First-In-First-Out(FIFO) rule is implemented whereas, in a priority queue, the values are removed based on priority. The element with the highest priority is removed first.

Operation on Priority Queues

Main Priority Queue Operations

Insert (key, data): Inserts data with a key to the priority queue. Elements are ordered based on key.
DeleteMin / DeleteMax: Remove and return the element with the smallest / largest key.
GetMinimum/GetMaximum: Return the element with the smallest/largest key without deleting it.

Auxiliary Priority Queues Operations

kth - Smallest/kth – Largest: Returns the kth -Smallest / kth –Largest key in the priority queue.
Size: Returns the number of elements in the priority queue.
Heap Sort: Sorts the elements in the priority queue based on priority (key).

Priority Queues Implementation

Before discussing the actual implementations, let us enumerate the possible options.

Unordered Array Implementation: Elements are inserted into the array without bothering the order. Deletions are performed by searching the minimum or maximum and deleting.
Unordered List Implementation: It is similar to array implementation but instead of array linked lists are used.
Ordered Array Implementation: Elements are inserted into the array in sorted order based on the key field. Deletions are performed only at one end of the array.
Ordered list implementation: Elements are inserted into the list in sorted order based on the key field. Deletions are performed at only one end, hence preserving the status of the priority queue. All other functionalities associated with a linked list ADT are performed without modification.
Binary Search Trees Implementation: Insertion and deletions are performed in a way such that the property of BST is reserved. Both the operations take O(logn) time on average and O(n) in the worst case.
Balanced Binary Search Trees Implementation: Insertion and deletions are performed such that the property of BST is reserved and the balancing factor of each node is -1, 0, or 1. Both operations take O(logn) time.
Binary Heap Implementation: We will be discussing this in detail. For now, just compare the time complexities.

Comparing Implementation

Heaps

A heap is a binary tree with some special properties.
The basic requirement of a heap is that the value of a node must be ≥ (or ≤) than the values of its children. This is called the heap property.
A heap also has the additional property that all leaf nodes should be at h or h – 1 level (where h is the height of the tree) for some h > 0 (complete binary trees).

That means the heap should form a complete binary tree (as shown below).

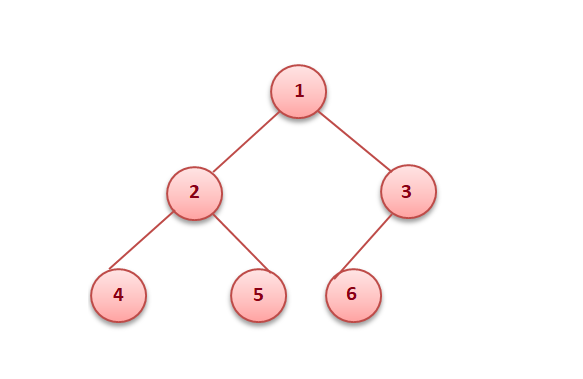
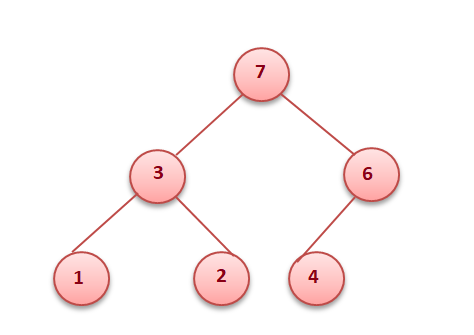
In the examples below, the left tree is a heap (each element is greater than its children) and the right is not a heap (since 11 is greater than 2 and 5 whereas the rest of the nodes are less than their children).

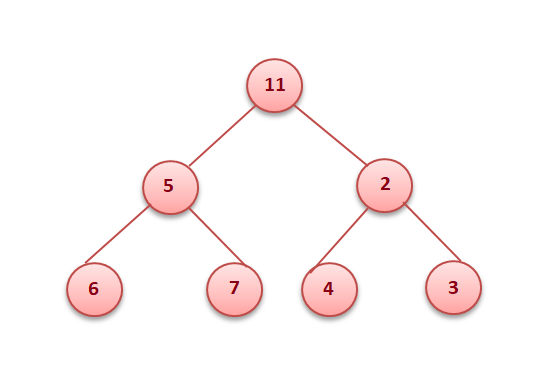
Types of heap

Min heap: The value of every node must be less than or equal to its children.

Max heap: The value of every node must be greater than or equal to its children.

Binary Heaps

In a binary heap, each node may have up to two children.
In practice, binary heaps are enough and we concentrate on binary min heaps and binary max heaps for the remaining discussion.

Representing heaps

Before looking at heap operations, let us see how heaps can be represented. One possibility is using arrays. Since heaps are forming complete binary trees, there will not be any wastage of locations. For the discussion below let us assume that elements are stored in an array, which starts at index 0. The previous max heap can be represented as:

Parent of a Node: For a node at index i, its parent is at index (i - 1) / 2. In the fig below element 6 is at the second index and its parent is at the 0th index.

Children of a Node : For a node at index i, its children are at index (2*i + 1) and (2i + 2). Like in the fig above 3 is at index 1 and has children at index 3 (2 * 1 + 1) and at index 4 (2 * 1 + 2) .

Getting the maximum/minimum element: The maximum element in a max heap, or the minimum element in a min-heap, is always the root node. It will be stored at the 0th index.

Heapify

Heapify is the process of creating a heap data structure from a binary tree. It is used to create a Min-Heap or a Max-Heap.

Let the input array be

Create a complete binary tree from the array
Start from the first index of the non-leaf node whose index is given by n / 2 - 1.

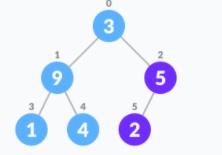
Set current element i as largest.
The index of the left child is given by 2i + 1 and the right child is given by 2i + 2.
If leftChild is greater than currentElement (i.e. element at the ith index), set leftChildIndex as largest.
If rightChild is greater than the element in largest, set rightChildIndex as largest.
Swap largest with currentElement.
Repeat steps 3-7 until the subtrees are also heapified.

The above steps are for Max-Heap. For Min-Heap, both leftChild and rightChild must be smaller than the parent for all nodes.

Pseudocode:

function  heapify(int i)

    largest = i
    l = 2 * i + 1                        //   Index of Left Child
    r = 2 * i + 2                        //   Index of Right Child
    
    if l < n && heap[i] < heap[l] 
        largest = l

    if (r < n && heap[largest] < heap[r]) 
        largest = r
   
    if largest is not equal to i 
        temp = heap[i]
        heap[i]  = heap[largest]
        heap[largest] = temp
        heapify(largest)

Inserting into a heap

Insertion into a heap can be done in two steps:

Insert the new element at the end of the tree.

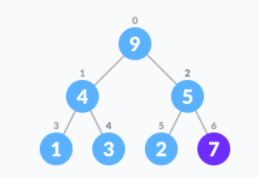
Move that element to its correct position in the heap.

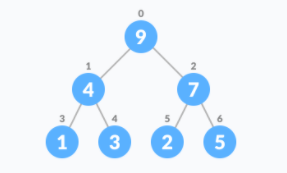
Pseudocode:

function insert(element) {

    //   add an element to the end of the heap list.
    heap.add(element)     

       childIndex = heap.length - 1
    parentIndex = (childIndex - 1) / 2

    while(childIndex > 0) 
        if heap[parentIndex] < heap[childIndex]) 

            temp = heap[parentIndex]
            heap[parentIndex] = heap[childIndex]
            heap[childIndex] = temp
            childIndex = parentIndex
            parentIndex = (childIndex - 1) / 2
    
        else 
            break

Delete Max Element from Max Heap

There are three easy steps to remove max from the max heap, we know that the 0th element would be the max.

Swap the 0th element with the last element.
Remove the last element from the heap.
Heapify the 0th element.

If you want to return the max element, then store it before replacing it with the last index, and return it in the end.

Pseudocode:

function removeMax(){

    if heap is empty
            print “heap is empty”
            return 
     
    retVal = heap[0]
    heap[0] = heap[heap.length - 1]
    heap.remove(heap.length - 1)

    if(heap.size() > 1) 
             heapify(0)
    
    return retVal

Implementation of Priority Queue

Priority queue can be implemented using an array, a linked list, a heap data structure, or a binary search tree.
Among these data structures, heap data structure provides an efficient implementation of priority queues.
Hence, we will be using the heap data structure to implement the priority queue.

Insertion and Deletion in a Priority Queue

The first step would be to represent the priority queue in the form of a max / min-heap. Once it is heapified, the insertion and deletion operations can be performed similarly to that in a Heap.

Heap Sort

Heap Sort is another example of an efficient sorting algorithm. Its main advantage is that it has a worst-case runtime of O(nlog(n)) regardless of the input data.
As the name suggests, Heap Sort relies heavily on the heap data structure - a common implementation of a Priority Queue.
Without a doubt, Heap Sort is one of the simplest sorting algorithms to implement, and coupled with the fact that it's a fairly efficient algorithm compared to other simple implementations, it's a common one to encounter.

Algorithm

The heap-sort algorithm inserts all elements (from an unsorted array) into a maxheap.
Note that heap sort can be done in-place with the array to be sorted.
Since the tree satisfies the Max-Heap property, then the largest item is stored at the root node.
Swap: Remove the root element and put it at the end of the array (nth position: n-1 index)
Put the last item of the tree (heap) at the vacant place.
Remove: Reduce the size of the heap by 1.
Heapify: Heapify the root element again so that we have the highest element at root.
The process is repeated until all the items in the list are sorted.

Consider the given illustrated example:

Applying heapsort to the unsorted array [12, 6, 10, 5, 1, 9]

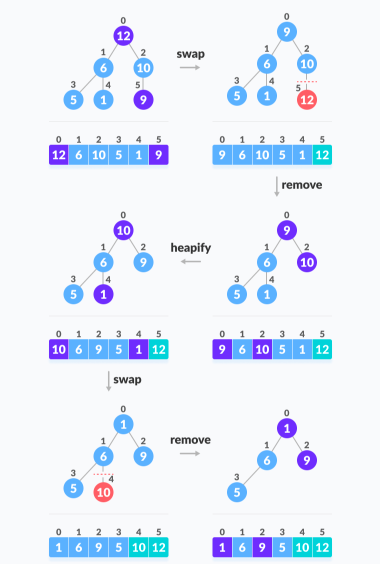
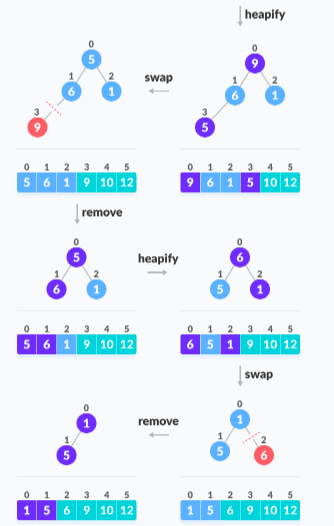
Pseudocode:

function heapSort(heap, startIndex, endIndex) 

       i = heap.length / 2 - 1
    while i is greater than or equal to 0
        heapify(input, i, input.length)
        i--    
    
    n = heap.length
       i = n-1
    while i is greater than equal to 0  
        //   Move current root to end 
           temp = heap[0]
         heap[0] = heap[i] 
         heap[i] = temp
         i--
 
     //   call heapify on the reduced heap 
      heapify(input, 0, i) 

function heapify(heap, index, arrLength) 

    largest = index
    left = 2 * index + 1
    right = 2 * index + 2
    
    if left < arrLength and heap[left] > heap[largest]
           largest = left

    if right < arrLength and input[right] > input[largest]
           largest = right
            
    if largest != index 
           k = input[index]
           input[index] = input[largest]
           input[largest] = k
           heapify(input, largest, arrLength)

Applications Of Priority Queues

It is used in data Compression: Huffman Coding Algorithm
Used in shortest path algorithms: Dijkstra’s Algorithm
Used in the minimum spanning tree algorithms: Prim’s algorithm
Used in Event-driven simulations: customers in a line.
Used in selection problems: kth - smallest element.