Cadence Design Systems interview experience Real time questions & tips from candidates to crack your interview
SDE - 1
Cadence Design Systems
3 rounds | 9 Coding
problems
Interview preparation journey
Preparation
Duration: 4 Months
Topics: Data Structures, Algorithms, OS, DBMS, Aptitude, OOPS
Tip
Tip 1 : Must do Previously asked Interview as well as Online Test Questions.
Tip 2 : Go through all the previous interview experiences from Codestudio and Leetcode.
Tip 3 : Do at-least 2 good projects and you must know every bit of them.
Application process
Where: Campus
Eligibility: Above 7 CGPA
Resume tip
Tip 1 : Have at-least 2 good projects explained in short with all important points covered.
Tip 2 : Every skill must be mentioned.
Tip 3 : Focus on skills, projects and experiences more.
Interview rounds
01
Round
Medium
Online Coding Test
Duration75 minutes
Interview date15 Jul 2020
Coding problem2
This was an online coding round where I had 2 questions to solve under 75 minutes. Both the coding questions were of Medium to Hard level of difficulty.
1. Smallest Window
Moderate
10m average time
90% success
0/80
Asked in companies



You are given two strings S and X containing random characters. Your task is to find the smallest substring in S which contains all the characters present in X.
Example:
Let S = “abdd” and X = “bd”.
The windows in S which contain all the characters in X are: 'abdd', 'abd', 'bdd', 'bd'.
Out of these, the smallest substring in S which contains all the characters present in X is 'bd'.
All the other substring have a length larger than 'bd'.
Problem approach
Approach 1 (Brute Force) :
1) Generate all substrings of string1.
2) For each substring, check whether the substring contains all characters of string2.
3) Finally, print the smallest substring containing all characters of string2.
TC : O(N^3), where N=length of the given string s1 and s2
SC : O(1)
Approach 2 (Sliding Window) :
We can use a simple sliding window approach to solve this problem.
The solution is pretty intuitive. We keep expanding the window by moving the right pointer. When the window has all
the desired characters, we contract (if possible) and save the smallest window till now.
The answer is the smallest desirable window.
Algorithm :
1) We start with two pointers, left and right initially pointing to the first element of the string S.
2) We use the right pointer to expand the window until we get a desirable window i.e. a window that contains all of the
characters of T
3) Once we have a window with all the characters, we can move the left pointer ahead one by one. If the window is
still a desirable one we keep on updating the minimum window size.
4) If the window is not desirable any more, we repeat step2 onwards.
TC : O(N+M) where N and M are the respective length of strings S and T.
SC : O(N+M)
2. K - Sum Path In A Binary Tree
Moderate
35m average time
65% success
0/80
Asked in companies



You are given a binary tree in which each node contains an integer value and a number ‘K’. Your task is to print every path of the binary tree with the sum of nodes in the path as ‘K’.
Note:
1. The path does not need to start or end at the root or a leaf, but it must go downwards (traveling only from parent nodes to child nodes).
2. Output the paths in the order in which they exist in the tree from left to right. Example: In the below example, path {1,3} is followed by {3,1} and so on.
Example:
For K = 4 and tree given below:
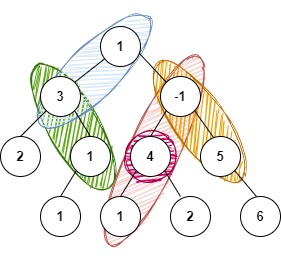
The possible paths are:
1 3
3 1
-1 4 1
4
-1 5
The sum of values of nodes of each of the above-mentioned paths gives a sum of 4.
Problem approach
The idea is simple: along the path, record all prefix sums in a hash table. For current prefix sum x, check if (x - target)
appears in the hash table.
Steps :
1) We will be using a unordered map which will be filled with various path sum.
2) For every node we will check if current sum and root’s value equal to k or not. If the sum equals to k then
increment the required answer by one.
3) Then we will add all those path sum in map which differs from current sum+root->data value by a constant integer
k.
4) Then we will be inserting the current sum + root->data value in the map.
5) We will recursively check for left and right subtrees of current root
6) After the right subtree is also traversed we will remove the current sum + root->data value from the map so that it
is not taken into consideration in further traversals of other nodes other than the current root’s.
TC : O(n) where n is the total number of nodes in the tree
SC : O(n)
02
Round
Medium
Video Call
Duration60 Minutes
Interview date15 Jul 2020
Coding problem4
This round had 2 questions of DS/Algo to solve under 60 minutes and 2 questions related to Operating Systems.
1. Validate BST
Moderate
25m average time
70% success
0/80
Asked in companies



Given a binary tree with N number of nodes, check if that input tree is Partial BST (Binary Search Tree) or not. If yes, return true, return false otherwise.
A binary search tree (BST) is said to be a Partial BST if it follows the following properties.
• The left subtree of a node contains only nodes with data less than and equal to the node’s data.
• The right subtree of a node contains only nodes with data greater than and equal to the node’s data.
• Both the left and right subtrees must also be partial binary search trees.
Example:
Input:
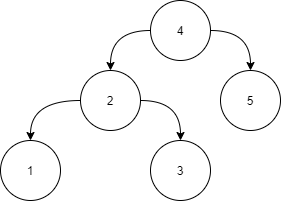
Answer:
Level 1:
All the nodes in the left subtree of 4 (2, 1, 3) are smaller
than 4, all the nodes in the right subtree of the 4 (5) are
larger than 4.
Level 2 :
For node 2:
All the nodes in the left subtree of 2 (1) are smaller than
2, all the nodes in the right subtree of the 2 (3) are larger than 2.
For node 5:
The left and right subtree for node 5 is empty.
Level 3:
For node 1:
The left and right subtree for node 1 are empty.
For node 3:
The left and right subtree for node 3 are empty.
Because all the nodes follow the property of a Partial binary
search tree, the above tree is a Partial binary search tree.
Problem approach
Approach 1 (Recursive Inorder Traversal) :
We know that the inorder traversal of a BST always gives us a sorted array , so if we maintain two variable Tree
Nodes "previous" and "current" , we should always have previous->val < current->value for a valid BST.
Steps :
1) Create a boolean recursive function with two parameters (root and prev) which will return true if our binary tree is a
BST or else it will return false.
2) If root is not null , call the recursive function with parameters (root->left,prev) and check if it return true or not.
3) For the prev node , check if at any point prev->val >= root->val if this condition is met , simply return false.
4) Update prev with root.
5) Call the recursive function again with parameters (root->right , prev)
TC : O(N) where N=number of nodes in the binary tree
SC : O(N)
Approach 2 (Iterative Inorder Traversal) :
We can also perfom an iterative inorder traversal of the Binary Tree using a stack and check the same condition that
we checked above i.e., at any point if prev->value >= current->value if this is met then simply return false.
Steps :
1) Take a stack of TreeNodes and a TreeNode prev with its initial value as NULL.
2) Run a loop till stack is not empty or root != NULL.
3) While pushing a root to the stack, push all its left descendants into the stack untill root != NULL.
4) Take current = stack.top() and pop it from the stack
5) Check if prev is NOT NULL and if prev->val >= curr->val , if this cond. is met simply return false.
6) Update prev with current.
7) Update root with root->right.
TC : O(N) where N=number of nodes in the binary tree
SC : O(N)
2. Longest Increasing Subsequence
Moderate
30m average time
65% success
0/80
Asked in companies



For a given array with N elements, you need to find the length of the longest subsequence from the array such that all the elements of the subsequence are sorted in strictly increasing order.
Strictly Increasing Sequence is when each term in the sequence is larger than the preceding term.
For example:
[1, 2, 3, 4] is a strictly increasing array, while [2, 1, 4, 3] is not.
Problem approach
Approach 1 (Naive Solution) :
1) The simplest approach to solve the problem is to generate all possible subarrays.
2) For each subarray, check if the difference between adjacent elements remains the same throughout or not.
3) Among all such subarrays satisfying the condition, store the length of the longest subarray and print it as the result.
TC : O(N^3), where N=size of the array
SC : O(1)
Approach 2 (Efficient Solution) :
1) Initialize a variable called res to store the length of the longest subarray forming an AP.
2) Iterate over remaining arrays and compare the current adjacent difference with the previous adjacent difference.
3) Iterate over the array, and for each element, calculate the difference between the current pair of adjacent elements
and check if it is equal to the previous pair of adjacent elements.
4) If found to be true, continue the ongoing subarray by incrementing res by 1.
5) Otherwise, consider a new subarray. Update the maximum length obtained so far, i.e. res by comparing it with the
length of the previous subarray.
6) Finally, return the res as the required answer.
TC : O(N), where N=size of the array
SC : O(1)
3. OS Question
Define Process and Threads in OS.
Problem approach
Process : A process is an instance of a program that is being executed. When we run a program, it does not execute
directly. It takes some time to follow all the steps required to execute the program, and following these execution
steps is known as a process.
A process can create other processes to perform multiple tasks at a time; the created processes are known as clone
or child process, and the main process is known as the parent process. Each process contains its own memory
space and does not share it with the other processes. It is known as the active entity.
Thread : A thread is the subset of a process and is also known as the lightweight process. A process can have more
than one thread, and these threads are managed independently by the scheduler. All the threads within one process
are interrelated to each other. Threads have some common information, such as data segment, code segment, files,
etc., that is shared to their peer threads. But contains its own registers, stack, and counter.
4. OS Question
What are the different types of semaphores ?
Problem approach
There are two main types of semaphores i.e. counting semaphores and binary semaphores.
1) Counting Semaphores :
These are integer value semaphores and have an unrestricted value domain. These semaphores are used to
coordinate the resource access, where the semaphore count is the number of available resources. If the resources
are added, semaphore count automatically incremented and if the resources are removed, the count is decremented.
2) Binary Semaphores :
The binary semaphores are like counting semaphores but their value is restricted to 0 and 1. The wait operation only
works when the semaphore is 1 and the signal operation succeeds when semaphore is 0. It is sometimes easier to
implement binary semaphores than counting semaphores.
03
Round
Hard
Video Call
Duration60 Minutes
Interview date15 Jul 2020
Coding problem3
In this round, I was asked 3 coding questions out of which I had to implement the first two and for the last question I was only asked the optimal approach. The main challenge in this round was to implement the first two questions in a production ready manner without any bugs and so I had to spent some time thinking about some Edge Cases which were important with respect to the question.
1. Next Greater Element
Moderate
20m average time
90% success
0/80
Asked in companies



You are given an array arr of length N. You have to return a list of integers containing the NGE(next greater element) of each element of the given array. The NGE for an element X is the first greater element on the right side of X in the array. Elements for which no greater element exists, consider the NGE as -1.
For Example :
If the given array is [1, 3, 2], then you need to return [3, -1, -1]. Because for 1, 3 is the next greater element, for 3 it does not have any greater number to its right, and similarly for 2.
Problem approach
Approach 1 (Naive Solution) :
1) Use two loops: The outer loop picks all the elements one by one.
2) The inner loop looks for the first greater element for the element picked by the outer loop.
3) If a greater element is found then that element is printed as next, otherwise, -1 is printed.
TC : O(N^2), where N=size of the array
SC : O(1)
Approach 2 (Using Stack) :
1) Push the first element to stack.
2) Pick rest of the elements one by one and follow the following steps in loop.
2.1) Mark the current element as next.
2.2) If stack is not empty, compare top element of stack with next.
2.3) If next is greater than the top element, Pop element from stack. next is the next greater element for
the popped element.
2.4) Keep popping from the stack while the popped element is smaller than next. next becomes the next
greater element for all such popped elements.
3) Finally, push the next in the stack.
4) After the loop in step 2 is over, pop all the elements from the stack and print -1 as the next element for them.
TC : O(N), where N=size of the array
SC : O(N)
2. Power Set
Easy
15m average time
85% success
0/40
Asked in companies



You are given a sorted array of 'N' integers. You have to generate the power set for this array where each subset of this power set is individually sorted.
A set is a well-defined collection of distinct elements. Power set P(ARR) of a set 'ARR' is defined as a set of all possible subsets of 'ARR'.
You have to return the array of subsets. The elements in the subset should be sorted in ascending order. The order of subsets in the array does not matter. Hence there can be more than 1 possible solution for a given array.
For example :
If we are given an array ARR=[1,2,3] then the power set P(ARR) of the set ARR is: [ [], [1], [2], [1,2], [3], [1,3], [2,3], [1,2,3] ]
Note :
For every subset 'X' present in power set P(ARR) of set ARR, X must be sorted i.e. in the example above:
P1(ARR) = [ [], [1], [2], [1,2], [3], [1,3], [2,3], [1,2,3] ]
P2(ARR) = [ [], [1], [1,2,3], [2], [1,2], [3], [1,3], [2,3] ]
P3(ARR) = [ [], [1], [2], [1,2], [3], [1,3], [2,3], [2,3,1] ]
P1(ARR) and P2(ARR) will be considered correct power sets but P3(ARR) will not be considered correct because there the last subset [2, 3, 1] is not sorted.
Problem approach
Given,a set of n elements I was supposed to print all the subsets of this set . I was famiiar with this question and had
already solved it in LeetCode and CodeStudio so coding it in the first go was not so hard for me .
Approach : I solved it using bitmasking . The main intuition was if I have a binary number like 1001 , I would take only
the 0th element and the 3rd element of the array .
Steps :
1) Run a loop from 0 to (2^n)-1 (as we have 2^n subsets for a set of n elements)
2) For every number , run a loop again from 0 to n-1 to check if the ith bit is set or not.
3) To check if the ith bit is set or not , simply check if (number & 2^i) > 0 or not
(where i ranges from 0 to n-1)
4) If (num & 2^i)==0 , ith bit is 0 i.e., do not take the ith element into the subset . Else if (num &2^i)>0 , ith bit is 1 i.e.,
take the ith element into the subset.
5) Finally put all the subsets into a vector and output the answer vector
TC : O(2^n)
SC : O(2^n)
3. Counting Sort
Easy
0/40
Asked in companies



Ninja is studying sorting algorithms. He has studied all comparison-based sorting algorithms and now decided to learn sorting algorithms that do not require comparisons.
He was learning counting sort, but he is facing some problems. Can you help Ninja implement the counting sort?
For example:
You are given ‘ARR’ = {-2, 1, 2, -1, 0}. The sorted array will be {-2, -1, 0, 1, 2}.
Problem approach
Answer : The easiest way to do this is to use external sorting.
Steps :
1) We divide our source file into temporary files of size equal to the size of the RAM and first sort these files.
2) Assume 1GB = 1024MB, so we follow following steps.
2.1) Divide the source file into 5 small temporary files each of size 200MB (i.e., equal to the size of ram).
2.2) Read input_file such that at most ‘runSize’ elements are read at a time. Do following for the every
run read in an array.
2.3) Sort the run using MergeSort.
2.4) Store the sorted array in a file. Lets say ‘i’ for ith file.
2.5) Merge the sorted files using the same approach used in Merge K sorted arrays.
Now we have sorted temporary files.
1) Pointers are initialized in each file
2) A new file of size 1GB (size of source file) is created.
3) First element is compared from each file with the pointer.
4) Smallest element is copied into the new 1GB file and pointer gets incremented in the file which pointed to this
smallest element.
5) Same process is followed till all pointers have traversed their respective files.
6) When all the pointers have traversed, we have a new file which has 1GB of sorted integers.
This is how any larger file can be sorted when there is a limitation on the size of primary memory (RAM).
TC : O(n * log n) , where n=size of the array
SC : O(runSize) , runSize is the space needed to store the array.

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 1
2 rounds | 5 problems
Interviewed by Cadence Design Systems
2770 views
0 comments
0 upvotes
SDE - 1
3 rounds | 10 problems
Interviewed by Cadence Design Systems
1855 views
0 comments
0 upvotes
QA Engineer
3 rounds | 4 problems
Interviewed by Cadence Design Systems
0 views
0 comments
0 upvotes
SDE - 1
3 rounds | 10 problems
Interviewed by Cadence Design Systems
1229 views
0 comments
0 upvotes
Companies with similar interview experiences
SDE - 1
2 rounds | 3 problems
Interviewed by BNY Mellon
6315 views
3 comments
0 upvotes
SDE - 1
3 rounds | 6 problems
Interviewed by BNY Mellon
0 views
0 comments
0 upvotes
SDE - 1
3 rounds | 5 problems
Interviewed by CIS - Cyber Infrastructure
2179 views
0 comments
0 upvotes







