Chegg Inc. interview experience Real time questions & tips from candidates to crack your interview
SDE - 1
Chegg Inc.
3 rounds | 7 Coding
problems
Interview preparation journey
Journey
I started my journey in coding from second year after being motivated from my seniors. I initially started my journey by learning basic programming languages. Later, I started giving contests on code forces and solving questions on it. I kept trying to be consistent in doing so. After 2-3 months I was able to solve some questions on code forces. Then in my third year, I studied core subjects like OS, DBMS, OOPS and CN in depth. In this manner, I was well prepared before the placement season.
Application story
This company visited to my campus the placement .
Why selected/rejected for the role?
i was rejected because i was not able to maintain the timing of the questions to be answer i should be more fast.
Preparation
Duration: 3 Months
Topics: Data Structures, Pointers, OOPS, System Design, Algorithms, Dynamic Programming
Tip
Tip 1 : Practice coding from Leetcode, Interview bit, at least 100 questions
Tip 2 : Practice any one automation framework includes design patterns
Application process
Where: Campus
Eligibility: Above 7 CGPA
Resume tip
Tip 1 : Restrict your resume to 1 page and write your practical work only
Tip 2 : Mention top topics like Selenium, Rest Assured Automation, Language used Java etc
Interview rounds
01
Round
Easy
Video Call
Duration60 Minutes
Interview date8 Sep 2022
Coding problem3
1. Technical Questions
How to find the pre order traversal of a tree?
State complexity of merge sort
Questions based on radix sort
Problem approach
Pre-order traversal of a tree is a way to visit and process the nodes of a tree in a specific order. The pre-order traversal follows the rule of visiting the root node, then recursively visiting the left subtree in pre-order, and finally recursively visiting the right subtree in pre-order.
how does radix sort work?
What are the different variants of radix sort, such as least significant digit (LSD) radix sort and most significant digit (MSD) radix sort?
What is the time complexity of radix sort?
What are the applications or use cases where radix sort can be useful?
Can you implement radix sort in a specific programming language, such as Python or C++?
What are the advantages and disadvantages of radix sort compared to other sorting algorithms, such as comparison-based sorting algorithms like merge sort or quicksort?
2. Preorder traversal of a BST
Moderate
15m average time
85% success
0/80
Asked in companies



You have been given an array/list 'PREORDER' representing the preorder traversal of a BST with 'N' nodes. All the elements in the given array have distinct values.
Your task is to construct a binary search tree that matches the given preorder traversal.
A binary search tree (BST) is a binary tree data structure that has the following properties:
• The left subtree of a node contains only nodes with data less than the node’s data.
• The right subtree of a node contains only nodes with data greater than the node’s data.
• Both the left and right subtrees must also be binary search trees.
Note:
It is guaranteed that a BST can be always constructed from the given preorder traversal. Hence, the answer will always exist.
Example:
From PREORDER = [20, 10, 5, 15, 13, 35, 30, 42] , the following BST can be constructed:
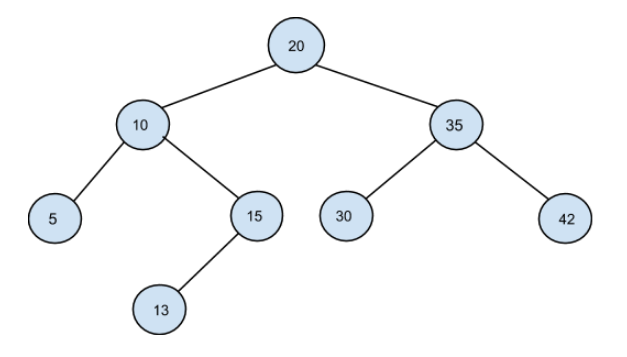
Problem approach
Converting a pre-order traversal of a binary tree into a binary search tree (BST) involves constructing a BST from the given pre-order traversal sequence. The pre-order traversal sequence represents the order in which the nodes are visited starting from the root node.
3. Check if number is Binary
Easy
10m average time
90% success
0/40
Asked in companies



Given a string of integers ‘bin’. Return 'true' if the string represents a valid binary number, else return 'false'. A binary number is a number that has only 0 or 1 in it.
Problem approach
To check if a given number is binary or not, you can follow these steps:
Convert the number to a string representation.
Iterate through each character in the string and check if it is either '0' or '1'. If any character is found that is not '0' or '1', then the number is not binary.
If all characters in the string are '0' or '1', then the number is binary.
02
Round
Medium
Video Call
Duration60 Minutes
Interview date8 Sep 2022
Coding problem2
1. Rearrange The Array
Easy
0/40
Asked in companies



You are given an array/list NUM of integers. You are supposed to rearrange the elements of NUM such that no two adjacent elements will be the same or find out if it not possible.
For example:
Input: arr[] = {1,1,1,2,2,2}
Output: {1,2,1,2,1,2}
Note: {2,1,2,1,2,1} is also valid because there are no two adjacent elements which are the same.
2. Number and Digits
Easy
15m average time
80% success
0/40
Asked in companies


You are given a positive number ‘N.’ You need to find all the numbers such that the sum of digits of those numbers to the number itself is equal to ‘N.’
For example:
You are given ‘N’ as 21, the only number whose sum of digits and the number itself equals 21 is 15 as 15 + 1 + 5 = 21. Hence the answer is [15].
Problem approach
Numbers and digits are related concepts that are used in mathematics to represent quantities and values.
A number is a mathematical concept that represents a quantity or value. Numbers can be classified into different types based on their properties, such as natural numbers (1, 2, 3, ...), integers (..., -3, -2, -1, 0, 1, 2, 3, ...), rational numbers (numbers that can be expressed as a ratio of two integers), real numbers (numbers that can be represented on a number line, including irrational numbers like π), and complex numbers (numbers of the form a + bi, where a and b are real numbers and i is the imaginary unit).
Digits, on the other hand, are symbols used to represent numbers in a positional number system. The most common positional number system is the decimal system, which uses ten digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) to represent all possible numbers. For example, the number 1234 in the decimal system is composed of the digits 1, 2, 3, and 4. The position of each digit in the number determines its place value, with the rightmost digit representing ones, the next digit to the left representing tens, the next representing hundreds, and so on.
Digits are also used in other positional number systems, such as binary (base-2), octal (base-8), and hexadecimal (base-16), which use different sets of digits to represent numbers. For example, the binary system uses only two digits, 0 and 1, to represent all possible numbers, while the hexadecimal system uses sixteen digits, 0-9 and A-F (where A represents 10, B represents 11, and so on), to represent numbers. The concept of digits is fundamental to understanding how numbers are represented and manipulated in different number systems.
03
Round
Easy
Video Call
Duration60 Minutes
Interview date8 Sep 2022
Coding problem2
1. Reverse the String
Easy
15m average time
85% success
0/40
Asked in companies



You are given a string 'STR'. The string contains [a-z] [A-Z] [0-9] [special characters]. You have to find the reverse of the string.
For example:
If the given string is: STR = "abcde". You have to print the string "edcba".
follow up:
Try to solve the problem in O(1) space complexity.
Problem approach
To reverse a string, you can use the following steps:
Convert the string to a list of characters to make it mutable.
Use two pointers, one at the beginning of the list and the other at the end of the list.
Swap the characters at the two pointers.
Move the pointers towards each other until they meet in the middle.
Convert the list of characters back to a string.
2. Puzzle
To identify the defective coin among 10 coins using a weight scale, you can follow these steps:
Divide the 10 coins into three groups: Group A with 3 coins, Group B with 3 coins, and Group C with 4 coins.
Weigh Group A against Group B using the weight scale.
If Group A and Group B have the same weight, then the defective coin must be in Group C. Move on to step 4.
If Group A and Group B have different weights, then the defective coin must be in one of these two groups. Let's assume without loss of generality that Group A is lighter than Group B (the opposite case can be handled in the same way). Move on to step 5.
Take any two coins from Group A and weigh them against each other. If one of them is lighter, then that coin is defective. If they have the same weight, then the third coin in Group A is defective.
Here's a summary of the steps:
Divide the 10 coins into Group A (3 coins), Group B (3 coins), and Group C (4 coins).
Weigh Group A against Group B.
If Group A and Group B have the same weight, go to step 4. Otherwise, go to step 5.
Weigh any two coins from Group C against each other. The lighter coin is defective.
Weigh any two coins from Group A against each other. If one of them is lighter, that coin is defective. Otherwise, the third coin in Group A is defective.
Using these steps, you can identify the defective coin among the 10 coins with just three weighings using the weight scale.

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 1
2 rounds | 5 problems
Interviewed by Chegg Inc.
1088 views
0 comments
0 upvotes
SDE - 1
3 rounds | 7 problems
Interviewed by Chegg Inc.
1145 views
0 comments
0 upvotes
SDE - 1
2 rounds | 4 problems
Interviewed by Chegg Inc.
1002 views
1 comments
0 upvotes
SDE - 1
3 rounds | 6 problems
Interviewed by Chegg Inc.
772 views
0 comments
0 upvotes
Companies with similar interview experiences
SDE - 1
5 rounds | 12 problems
Interviewed by Amazon
114869 views
24 comments
0 upvotes
SDE - 1
4 rounds | 5 problems
Interviewed by Microsoft
58030 views
5 comments
0 upvotes
SDE - 1
3 rounds | 7 problems
Interviewed by Amazon
35057 views
7 comments
0 upvotes





