SDE - 1

You are given an array/list 'prices' where the elements of the array represent the prices of the stock as they were yesterday and indices of the array represent minutes. Your task is to find and return the maximum profit you can make by buying and selling the stock. You can buy and sell the stock only once.

Note:

You can’t sell without buying first.

For Example:

For the given array [ 2, 100, 150, 120],
The maximum profit can be achieved by buying the stock at minute 0 when its price is Rs. 2 and selling it at minute 2 when its price is Rs. 150.
So, the output will be 148.

You are given the root node of a binary tree.

Return 'true' if it is a height balanced binary tree.

Note:

Height of a tree is the maximum number of nodes in a path from the node to the leaf node.

An empty tree is a height-balanced tree. A non-empty binary tree is a height-balanced binary tree if
1. The left subtree of a binary tree is already the height-balanced tree.
2. The right subtree of a binary tree is also the height-balanced tree.
3. The difference between heights of left subtree and right subtree must not more than ‘1’.

Example:

Input: Consider the binary tree given below:

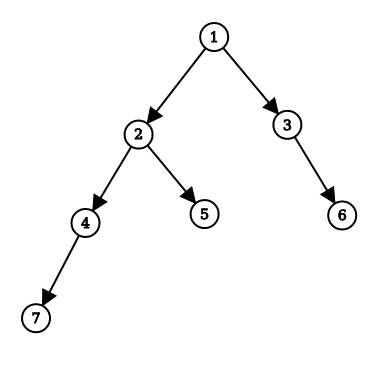
Output: 'true'

Explanation:
Consider subtree at Node ( 7 ) 
Left subtree height is ‘0’ and right subtree height is ‘0’, the absolute height difference is ‘0-0 = 0’ and ‘0’ is not more than ‘1’ so subtree at Node ( 7 ) is a height-balanced binary tree. 
Same for subtrees at Nodes ( 5, 6 ). 

Consider subtree at Node ( 4 ) 
Left subtree height is ‘1’ and right subtree height is ‘0’, the absolute height difference is ‘1-0 = 1’ and ‘1’ is not more than ‘1’ so subtree at Node ( 4 ) is a height-balanced binary tree.
Same for subtree at Node ( 3)

Consider subtree at Node ( 2 ) 
Left subtree height is ‘2’ and right subtree height is ‘1’, the absolute height difference is ‘2-1 = 1’ and ‘1’ is not more than ‘1’ so subtree at Node ( 2 ) is a height-balanced binary tree.

Consider subtree at Node ( 1 ) 
Left subtree height is ‘3’ and right subtree height is ‘2’, the absolute height difference is ‘3-2 = 1’ and ‘1’ is not more than ‘1’ so subtree at Node ( 1 ) is a height-balanced binary tree.

Because the root node ( 1 ) is a height-balanced binary tree, so the complete tree is height-balanced.

You are given an arbitrary binary tree consisting of N nodes where each node is associated with a certain integer value from 1 to 9. Consider each root to leaf path as a number.

For example:

       1
      /  \
     2    3

The root to leaf path 1->2 represents the number 12.
The root to leaf path 1->3 represents the number 13.

Your task is to find the total sum of all the possible root to leaf paths.

In the above example,

The total sum of all the possible root to leaf paths is 12+13 = 25

Note:

The output may be very large, return the answer after taking modulus with (10^9+7).

Given a Binary Search Tree (BST) and a range [min, max], remove all keys which are outside the given range. The modified tree should also be BST.

You are given an array/list of ‘N’ integers. You are supposed to return the maximum sum of the subsequence with the constraint that no two elements are adjacent in the given array/list.

Note:

A subsequence of an array/list is obtained by deleting some number of elements (can be zero) from the array/list, leaving the remaining elements in their original order.

You are given an integer 'N'. For a given 'N' x 'N' chessboard, find a way to place 'N' queens such that no queen can attack any other queen on the chessboard.

A queen can be killed when it lies in the same row, or same column, or the same diagonal of any of the other queens. You have to print all such configurations.