Cvent interview experience Real time questions & tips from candidates to crack your interview
SE-1
Cvent
4 rounds | 4 Coding
problems
Interview preparation journey
Journey
It was an on-campus opportunity consisting of five rounds. The first round was an MCQ-based assessment focused on aptitude, while the second round included questions on simple computer science concepts, DSA, OS, and DBMS, which were fairly easy. Candidates who cleared these rounds moved on to interviews. The third round, my first interview, focused on my projects, including a mobile app and a Chrome extension I built using external APIs. They asked about my experience with mobile app development and RESTful APIs, followed by a coding challenge to implement a queue without using built-in queue functions, which I found straightforward. The fourth round delved deeper into my projects, specifically React Native, and included the LRU Cache problem, along with a variation that involved modifying cache priorities. The final round was with a senior manager, where I was asked about myself, my expectations from Cvent, and a medium-level problem, “Snake and Ladder.” Although I couldn’t fully code the solution, I clearly explained my approach, which they appreciated. Ultimately, I was selected as a full-time employee.
Application story
It was an on-campus opportunity. I applied and got shortlisted for the online assessment (OA), which then led to 5 offline rounds: 1 round of aptitude and another with basic computer science course questions. After that, I had 3 coding interviews.
Why selected/rejected for the role?
I solved every DSA problem I encountered and worked on projects in React and Java, which led to my selection, as every company uses Java.
Preparation
Duration: 8 months
Topics: Data Structures, Pointers, OOPS, React, Database Management systems
Tip
Tip 1: Be consistent.
Tip 2: Don't give up.
Tip 3: It seems hard, but it's not.
Application process
Where: Campus
Eligibility: No criteria, (Salary Package - 15 LPA)
Resume tip
Tip 1: Add projects that involve full-stack development.
Tip 2: Add points on DSA.
Interview rounds
01
Round
Medium
Online Coding Interview
Duration45 minutes
Interview date16 Oct 2022
Coding problem1
The process started at 8 AM and ended at 7 PM. I didn't get time for lunch. However, it was a good interview experience, as the interviewers were calm and gentle, guiding me through the approaches. They also focused more on whether I was able to build a solution and less on the code I wrote.
1. Basic Reasoning questions
Problem approach
Tip 1: Presence of mind
Tip 2: Math
Tip 3: Reasoning
02
Round
Medium
Face to Face
Duration45 Minutes
Interview date16 Oct 2022
Coding problem1
The process started at 8 AM and ended at 7 PM. I didn't get time for lunch. However, it was a good interview experience, as the interviewers were calm and gentle, guiding me through the approaches. They also focused more on whether I was able to build a solution and less on the code I wrote.
1. LRU Cache
Moderate
0/80
Asked in companies



Design a data structure that satisfies the constraints of a Least Recently Used (LRU).
1. Get(int num): If the key exists, it will return the value of the key stored. Else, return -1.
2. Put(int key, int value): If the key already exists, update the value of the key. Else add the key-value pair to the cache. If the number of keys is more than the capacity for this operation, delete the least recently key used.
Example:
For the following input:
4 2
2 1 4
1 1
1 4
We will initialize an empty LRU cache for the first operation with a maximum capacity of 2.
For the first operation, we need to add a key-value pair (1,4) to the cache.
For the second operation, we need to return the value stored for key 1, i.e., 4
For the third operation, we need to return -1, as we don't have any key 4 in the cache.
So, the final output will be:
4 -1
Problem approach
Intuition:
The intuition is to maintain a fixed-size cache of key-value pairs using a doubly linked list and an unordered map. When accessing or adding a key-value pair, it moves the corresponding node to the front of the linked list, making it the most recently used item. This way, the least recently used item is always at the end of the list. When the cache is full and a new item is added, it removes the item at the end of the list (least recently used) to make space for the new item, ensuring the LRU property is maintained.
Explanation:
Node Class:
This is a nested class representing a doubly linked list node.
Each node contains an integer key, an integer value, and pointers to the previous and next nodes in the linked list.
LRUCache Class:
This is the main LRU Cache class.
It has a fixed capacity (cap) that is specified during its instantiation.
It uses an unordered_map named m to store key-value pairs, where the key is the integer key, and the value is a pointer to the corresponding Node.
head and tail Nodes:
The LRUCache class has two dummy nodes: head and tail.
These nodes act as sentinels in the doubly linked list, helping to simplify the edge cases and avoid dealing with null pointers.
head is the first node in the linked list, and tail is the last node.
addNode Function:
This function is used to add a new node to the front of the doubly linked list (right after head).
It takes a Node* newnode as input, representing the node to be added.
The function updates the pointers of the new node, the previous first node, and head to include the new node as the new first node.
deleteNode Function:
This function is used to delete a node from the doubly linked list.
It takes a Node* delnode as input, representing the node to be deleted.
The function updates the pointers of the previous and next nodes to exclude the node to be deleted, effectively removing it from the linked list.
get Function:
This function is used to retrieve a value from the cache based on the given key.
If the key exists in the cache (m.find(key) != m.end()), it retrieves the corresponding node (resNode), extracts its value (ans), and performs the following steps:
Erase the key-value pair from the m unordered map.
Delete the node from its current position in the linked list using deleteNode.
Add the node to the front of the linked list using addNode, making it the most recently used node.
Update the m map to store the key with the most recently used node.
If the key doesn't exist in the cache, it returns -1.
put Function:
This function is used to insert or update a key-value pair in the cache.
If the key already exists in the cache, it updates the value by performing the following steps:
Erase the existing key-value pair from the m unordered map.
Delete the corresponding node from its current position in the linked list using deleteNode.
If the cache is full (i.e., m.size() == cap), it removes the least recently used node from the cache by erasing the key-value pair from the m map and deleting the node from the end of the linked list using deleteNode.
After handling the eviction (if needed), it creates a new node using a new Node(key, value) and adds it to the front of the linked list using addNode.
Finally, it updates the m map to store the key with the newly added node.
03
Round
Medium
Face to Face
Duration45 minutes
Interview date16 Oct 2022
Coding problem1
The medium-level questions took around 45 minutes in the evening. The interviewers helped a lot when I was building the solution.
1. Snake and Ladder
Moderate
30m average time
60% success
0/80
Asked in companies



You have been given a Snake and Ladder Board with 'N' rows and 'N' columns with the numbers written from 1 to (N*N) starting from the bottom left of the board, and alternating direction each row.
For example
For a (6 x 6) board, the numbers are written as follows:
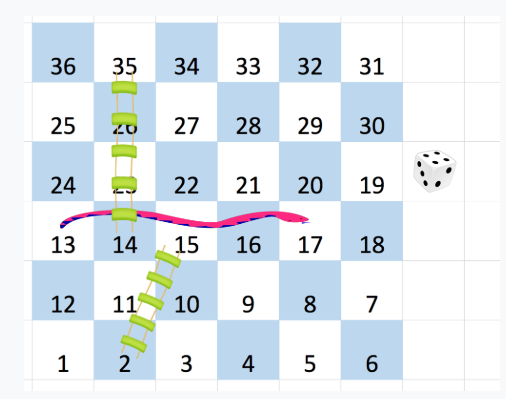
You start from square 1 of the board (which is always in the last row and first column). On each square say 'X', you can throw a dice which can have six outcomes and you have total control over the outcome of dice throw and you want to find out the minimum number of throws required to reach the last cell.
Some of the squares contain Snakes and Ladders, and these are possibilities of a throw at square 'X':
You choose a destination square 'S' with number 'X+1', 'X+2', 'X+3', 'X+4', 'X+5', or 'X+6', provided this number is <= N*N.
If 'S' has a snake or ladder, you move to the destination of that snake or ladder. Otherwise, you move to S.
A board square on row 'i' and column 'j' has a "Snake or Ladder" if board[i][j] != -1. The destination of that snake or ladder is board[i][j].
Note :
You can only take a snake or ladder at most once per move: if the destination to a snake or ladder is the start of another snake or ladder, you do not continue moving - you have to ignore the snake or ladder present on that square.
For example, if the board is:
-1 1 -1
-1 -1 9
-1 4 -1
Let's say on the first move your destination square is 2 [at row 2, column 1], then you finish your first move at 4 [at row 1, column 2] because you do not continue moving to 9 [at row 0, column 0] by taking the ladder from 4.
A square can also have a Snake or Ladder which will end at the same cell.
For example, if the board is:
-1 3 -1
-1 5 -1
-1 -1 9
Here we can see Snake/Ladder on square 5 [at row 1, column 1] will end on the same square 5.
Problem approach
Intuition
The intuition behind this code is that it uses a breadth-first search (BFS) algorithm to find the minimum number of moves required to reach the last cell of the board from the first cell. BFS is an algorithm that explores all the vertices of a graph or all the nodes of a tree level by level.
Approach
The method starts by creating a vector of pairs called "cells" that store the row and column of each cell in the board. It also creates a vector of integers called "dist" that stores the minimum number of moves required to reach each cell and initializes it to -1.
It then uses a queue to keep track of the cells to be visited and starts by pushing the first cell (cell 1) into the queue. The method then enters a while loop that continues until the queue is empty. In each iteration of the loop, it takes the front element of the queue, which is the current cell, and pops it from the queue.
For the current cell, the method loops through all the possible next cells which are from curr+1 to min(curr+6,n*n) (because in each move we can move to a dice roll max 6 steps) and checks if the minimum number of moves required to reach that cell has not been assigned yet. If it has not been assigned yet, the method assigns the minimum number of moves required to reach that cell as the minimum number of moves required to reach the current cell plus one. It also pushes the next cell into the queue to be visited in the next iteration.
The method then continues this process until all the cells have been visited, and the minimum number of moves required to reach each cell has been assigned. Finally, the method returns the minimum number of moves required to reach the last cell, which is stored in dist[n*n].
04
Round
Medium
Face to Face
Duration45 minutes
Interview date16 Oct 2022
Coding problem1
Medium questions which took around 45 minutes in the evening. The interviewers help a lot when u are building a solution.
1. Queue Using Two Stacks
Easy
15m average time
85% success
0/40
Asked in companies



You will be given ‘Q’ queries. You need to implement a queue using two stacks according to those queries. Each query will belong to one of these three types:
1 ‘X’: Enqueue element ‘X’ into the end of the nth queue. Returns true after the element is enqueued.
2: Dequeue the element at the front of the nth queue. Returns -1 if the queue is empty, otherwise, returns the dequeued element.
Note:
Enqueue means adding an element to the end of the queue, while Dequeue means removing the element from the front of the queue.
Problem approach
Intuition
The problem is about simulating a queue using two stacks. A queue operates on a First-In-First-Out (FIFO) basis, while a stack operates on a Last-In-First-Out (LIFO) basis. To emulate a queue using two stacks, the idea is to maintain one stack (stack1) for inserting new elements and another stack (stack2) for retrieving elements in the correct order. By only transferring elements between the two stacks when necessary, we can achieve efficient queue operations.
Approach
Push Operation:
Simply push the new element onto stack1. This operation is efficient (O(1)) since no element rearrangement is needed during insertion.
Pop Operation:
If stack2 is not empty, pop the element directly from stack2.
If stack2 is empty, transfer all elements from stack1 to stack2 by popping from stack1 and pushing onto stack2. This effectively reverses the order of elements to match the FIFO order required by the queue.
After the transfer, pop from stack2.
Peek Operation:
Similar to the pop operation: If stack2 is empty, transfer elements from stack1 to stack2 and return the top element from stack2. If stack2 already contains elements, just peek the top without transferring.
Empty Operation:
Return true if both stack1 and stack2 are empty, indicating that the queue has no elements. Push Operation:
Simply push the new element onto stack1. This operation is efficient (O(1)) since no element rearrangement is needed during insertion.
Pop Operation:
If stack2 is not empty, pop the element directly from stack2.
If stack2 is empty, transfer all elements from stack1 to stack2 by popping from stack1 and pushing onto stack2. This effectively reverses the order of elements to match the FIFO order required by the queue.
After the transfer, pop from stack2.
Peek Operation:
Similar to the pop operation: If stack2 is empty, transfer elements from stack1 to stack2 and return the top element from stack2. If stack 2 already contains elements, just peek at the top without transferring.
Empty Operation:
Return true if both stack1 and stack2 are empty, indicating that the queue has no elements.

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 1
4 rounds | 5 problems
Interviewed by Cvent
1176 views
0 comments
0 upvotes
SDE - 2
5 rounds | 5 problems
Interviewed by Cvent
1288 views
0 comments
0 upvotes
SDE - 1
4 rounds | 7 problems
Interviewed by Cvent
1207 views
0 comments
0 upvotes
Full Stack Engineer
3 rounds | 4 problems
Interviewed by Cvent
677 views
0 comments
0 upvotes



