DP World interview experience Real time questions & tips from candidates to crack your interview
SDE - 2
DP World
4 rounds | 5 Coding
problems
Interview preparation journey
Journey
I prepared for the interview by practicing medium-level questions on Trees and Arrays. For 10 days before the interview, I solved 5 questions daily (2 easy and 3 medium).
Application story
I applied through LinkedIn and also reached out to HR via LinkedIn. After a few days, HR processed my resume and asked for my availability.
Why selected/rejected for the role?
I got rejected because I was not able to provide an optimal solution to the graph theory question, even though I gave an optimal solution to the system design question.
Preparation
Duration: 1 month
Topics: Arrays, BST, Trees, Recursion, Math, Hashing, System Design concepts like sharding, and design patterns.
Tip
Tip 1: Contribute to open source if you don’t have much experience to showcase.
Tip 2: Prepare for DSA consistently for at least 3 months.
Application process
Where: Linkedin
Eligibility: No criteria, (Salary Package - 27 LPA)
Resume tip
Tip 1: Only write about what you have prepared.
Tip 2: Having projects is the icing on the cake.
Interview rounds
01
Round
Easy
Online Coding Interview
Duration60 minutes
Interview date4 Jan 2025
Coding problem2
1. Remove All Occurrences
Easy
0/40
Asked in company

You are given an array 'A' of length 'N' and an element 'E'.
Return a new array containing all elements of 'A' except for all occurrences of 'E'. The order of the remaining elements should be preserved.
For Example :
Let 'N' = 6, 'A' = [1, 2, 2, 3, 4, 2], 'E' = 2.
The resulting array after removing all occurrences of 2 is [1, 3, 4].
Problem approach
We can use two pointers, i and j, where i is the slow runner and j is the fast runner.
2. First Missing Positive
Moderate
18m average time
84% success
0/80
Asked in companies



You are given an array 'ARR' of integers of length N. Your task is to find the first missing positive integer in linear time and constant space. In other words, find the lowest positive integer that does not exist in the array. The array can have negative numbers as well.
For example, the input [3, 4, -1, 1] should give output 2 because it is the smallest positive number that is missing in the input array.
Problem approach
We can solve the problem by iterating through the numbers from 1 to n and using linear search to determine whether each number is in the array. The first number we cannot find is the smallest missing integer. This approach results in quadratic time complexity.
02
Round
Easy
Video Call
Duration60 minutes
Interview date10 Jan 2025
Coding problem1
1. Distinct Subsequences
Moderate
10m average time
80% success
0/80
Asked in companies



You have been given string 'S' of length 'N' that may contain duplicate alphabets. Your task is to return the count of distinct subsequences of it.
For example:
For the given string “deed” :
The possible subsequences are {“”}, {“d”}, {“e”}, {“de”}, {“e”}, {“de”}, {“ee”}, {“dee”}, {“d”}, {“dd”}, {“ed”}, {“ded”}, {“ed”}, {“ded”}, {“eed”} and {“deed”}.
As, {“d”}, {“e”}, {“de”}, {“ed”} and {“ded”} are repeated.
The distinct subsequences are {“”}, {“d”}, {“e”}, {“de”}, {“ee”}, {“dee”}, {“dd”}, {“ed”}, {“ded”}, {“eed”} and {“deed”}
Thus, the output will be 11.
Note:
As the answer can be large, return your answer modulo 10^9 + 7.
Problem approach
Define a function called recurse that takes in two integer values, i and j, where i represents the current character to be processed in the string S and j represents the current character in the string T.
Initialize a dictionary called memo to cache the results of our different recursive calls.
Check the base cases:
If either string is finished, return 0 or 1 depending on whether the entire string T has been processed successfully.
Another base case to consider is if the remaining length of string S is less than that of string T; in this case, a match is impossible, so prune the recursion and return 0.
Next, check if the current pair of indices (i, j) exists in the dictionary. If it does, return the cached value.
If not, proceed with normal processing by comparing the characters S[i] and T[j].
Store the result of recurse(i + 1, j) in a variable; as explained above, this result is needed regardless of whether the characters match.
If the characters match, add the result of recurse(i + 1, j + 1) to this variable.
Finally, store this variable’s value in the dictionary with the key (i, j) and return it as the answer.
03
Round
Easy
Video Call
Duration60 minutes
Interview date17 Jan 2025
Coding problem1
1. Longest Palindromic Substring
Moderate
35m average time
78% success
0/80
Asked in companies



You are given a string ‘S’ of length ‘N’.
You must return the longest palindromic substring in ‘S’.
Note: Return any of them in case of multiple substrings with the same length.
Example:
Input: ‘S’ =’badam’
Output: ‘ada’
‘ada’ is the longest palindromic substring, and it can be proved that it is the longest possible palindromic substring.
Problem approach
Count the number of occurrences of each word using a hashmap
(Can use a Counter in Python).
Initialize answer=0, central=false. The answer will denote
The number of words in the final string and
The boolean variable central will denote whether we have a central word.
For each palindromic word, do the following. If count[word] is even,
increasethe answer by count[word]. Otherwise, if count[word] is odd,
increase answer by count[word]−1 and set central=true (we can use the
word as a central word).
For each non-palindrome word such that word[0] (we need this condition to consider each pair only once and not twice,
e.g. we don't want to consider both ba and ab separately)
increase answer by 2⋅min(count[word],count[reversedWord])
(we use min(count[word],count[reversedWord]) pairs of the corresponding words).
If central=true, increase answer by 1.
Return 2⋅answer. (Because each word has a length of 2).
04
Round
Easy
HR Round
Duration60 minutes
Interview date24 Jan 2025
Coding problem1
1. Rabbits In Forest
Easy
15m average time
85% success
0/40
Asked in companies


In a forest, each rabbit has some color. Some subset of rabbits (possibly all of them) tell you how many other rabbits have the same color as them. Those answers are placed in an array/list named ‘ANSWERS.’
Return the minimum number of rabbits that could be in the forest.
For Example :
Given:-
‘N’ = 3, ‘ANSWERS’ = [2,2,2]
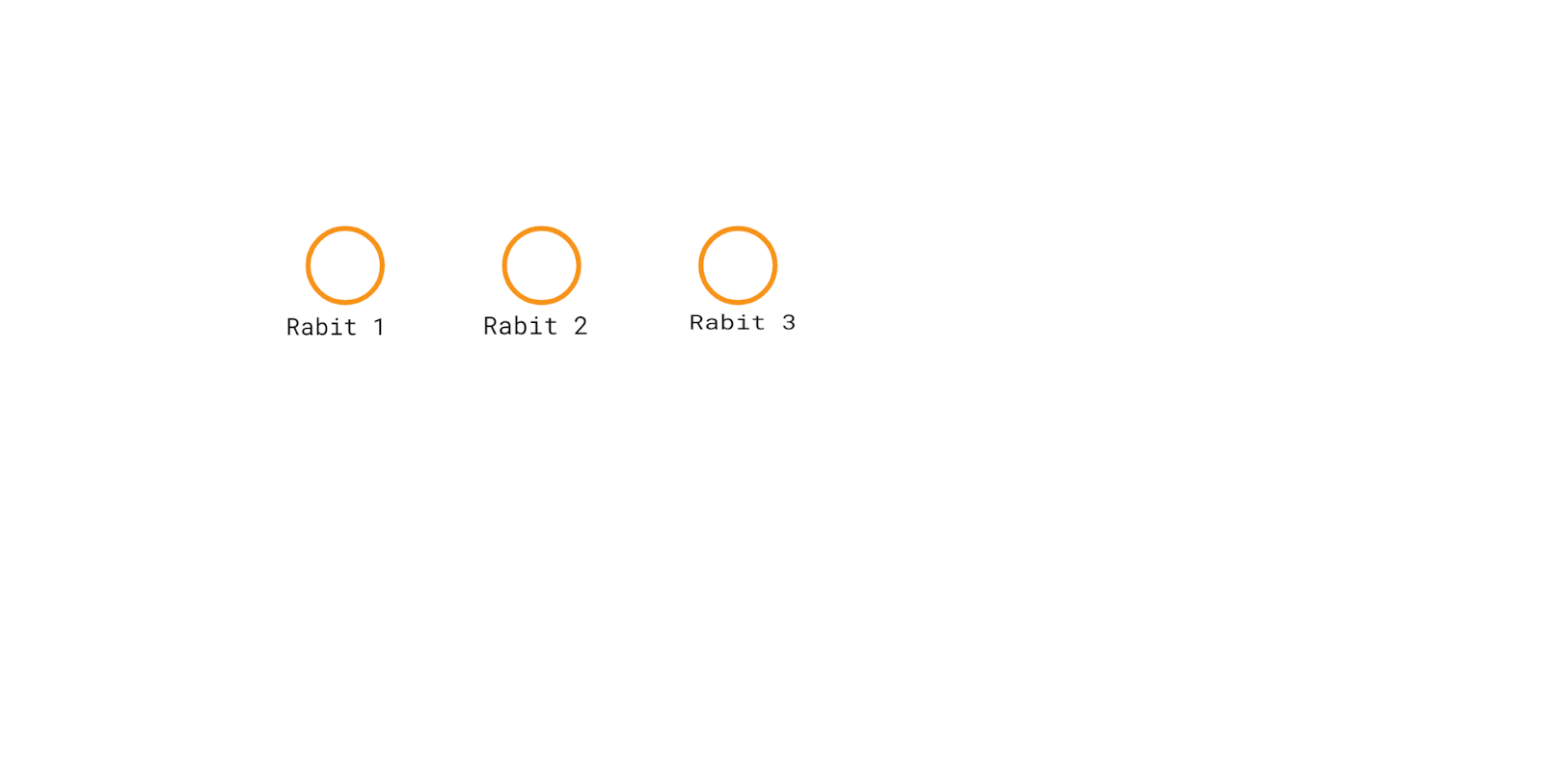
There are a total of 3 rabbits because each of the ‘ANSWERS[i]’ tells that there are two more rabbits just like them with the same color.

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 2
1 rounds | 2 problems
Interviewed by DP World
4053 views
0 comments
0 upvotes
SDE - 2
3 rounds | 3 problems
Interviewed by DP World
2649 views
0 comments
0 upvotes
SDE - 1
4 rounds | 8 problems
Interviewed by Amazon
8770 views
0 comments
0 upvotes
SDE - Intern
1 rounds | 3 problems
Interviewed by Amazon
3406 views
0 comments
0 upvotes
Companies with similar interview experiences
SDE - 2
5 rounds | 12 problems
Interviewed by Walmart
29738 views
8 comments
0 upvotes
SDE - 2
3 rounds | 5 problems
Interviewed by Amazon
6727 views
1 comments
0 upvotes
SDE - 2
6 rounds | 8 problems
Interviewed by Amazon
5224 views
0 comments
0 upvotes




