FlexiEle Consulting Services (FE) interview experience Real time questions & tips from candidates to crack your interview
Fullstack developer Intern
FlexiEle Consulting Services (FE)
2 rounds | 5 Coding
problems
Interview preparation journey
Journey
My journey into full-stack development began with mastering the fundamentals of HTML, CSS, and JavaScript, which provided a solid foundation for building web applications. From there, I delved into frameworks like React and Node.js to enhance my skill set. Applying these technologies, I created impactful projects such as QuizMaster, a platform for creating and sharing quizzes, and an e-commerce app with seamless cart functionality. I also explored data science and AI by working on projects like Brain Tumor Detection using CNNs and Credit Card Fraud Detection using XGBoost, which helped me integrate machine learning techniques with software development.
Platforms like GitHub and Indeed served as stepping stones, providing resources and internship opportunities, including a research internship at MAIT and a summer internship at Cantilever. These experiences allowed me to refine my problem-solving abilities and build production-ready applications. Preparing for internships and roles involved revisiting core concepts like data structures, algorithms, and design patterns, alongside practicing coding problems and developing AI-based solutions. This journey has underscored the importance of consistency, curiosity, and hands-on practice, which has shaped my passion for technology and innovation.
Application story
I came across the internship opening on Internshala while actively searching for full-stack development opportunities. The application process was straightforward—I submitted my resume along with a cover letter highlighting my projects and skills. After being shortlisted, I received further instructions for the next steps. Eventually, I was invited for an interview to discuss my technical knowledge, problem-solving approach, and past experiences. The process was smooth and well-structured, allowing me to effectively showcase my capabilities.
Why selected/rejected for the role?
I was not selected for the role because I struggled to solve one particular question related to graphs during the interview. While I had a strong understanding of most of the concepts, this question challenged me, and I was unable to come up with an optimal solution on the spot. However, I view this as a valuable learning experience. It highlighted areas where I need further improvement, particularly in graph theory and problem-solving under pressure. I am now actively revisiting these concepts and practicing more problems to ensure I'm better prepared for future opportunities.
Preparation
Duration: 1 months
Topics: Arrays, Strings, Linked Lists, Trees, Hashmap, OOP, Dynamic Programming
Tip
Tip 1: Understand common patterns, such as sliding windows and prefix sums, for optimization.
Tip 2: Solve problems related to binary search tree operations (insertion, deletion, search).
Tip 3: Focus on dynamic programming techniques for problems like the longest common subsequence.
Application process
Where: Campus
Eligibility: Have relevant skills such as Express.js, JavaScript, MySQL, Node.js, and ReactJS. (Salary: 13 LPA)
Resume tip
Tip 1: Add factual information about the projects you’ve worked on.
Tip 2: Only mention the skills you actually possess, and avoid listing fake ones.
Interview rounds
01
Round
Medium
Online Coding Test
Duration45 minutes
Interview date1 Nov 2024
Coding problem2
1. Longest Substring with At Most K Distinct Characters
Moderate
20m average time
80% success
0/80
Asked in companies



You are given a string 'str' and an integer ‘K’. Your task is to find the length of the largest substring with at most ‘K’ distinct characters.
For example:
You are given ‘str’ = ‘abbbbbbc’ and ‘K’ = 2, then the substrings that can be formed are [‘abbbbbb’, ‘bbbbbbc’]. Hence the answer is 7.
Problem approach
Step 1: I started by thinking about how to approach this problem using two-pointers. Initially, I set both the left and right pointers at the start of the string and considered expanding the window by moving the right pointer to the right.
Step 2: I realized that as the window expanded, I needed to track how many distinct characters were inside it. So, I used a hashmap (or dictionary) to count the frequency of each character within the window.
Step 3: As I moved the right pointer, I kept updating the hashmap with the character counts. If the number of distinct characters (i.e., the size of the hashmap) ever exceeded k, I knew I needed to shrink the window. So, I moved the left pointer to the right until the window contained at most k distinct characters again.
Step 4: While doing this, I kept track of the maximum length of the window that satisfied the condition (i.e., at most k distinct characters).
Step 5: This approach only required one pass through the string, making it much more efficient (O(n)) compared to using nested loops or sorting.
2. Merge Intervals
Moderate
20m average time
80% success
0/80
Asked in companies



You are given N number of intervals, where each interval contains two integers denoting the start time and the end time for the interval.
The task is to merge all the overlapping intervals and return the list of merged intervals sorted by increasing order of their start time.
Two intervals [A,B] and [C,D] are said to be overlapping with each other if there is at least one integer that is covered by both of them.
For example:
For the given 5 intervals - [1, 4], [3, 5], [6, 8], [10, 12], [8, 9].
Since intervals [1, 4] and [3, 5] overlap with each other, we will merge them into a single interval as [1, 5].
Similarly, [6, 8] and [8, 9] overlap, merge them into [6,9].
Interval [10, 12] does not overlap with any interval.
Final List after merging overlapping intervals: [1, 5], [6, 9], [10, 12].
Problem approach
Step 1: I began by considering how to handle the intervals. The first approach that came to mind was sorting the intervals based on their start times. This seemed like a natural solution because, if the intervals are sorted, any overlapping intervals will be next to each other.
Step 2: Once the intervals were sorted, I knew I had to check each interval against the last merged interval. If the current interval started before the last merged interval ended, I would merge them. This meant updating the end of the merged interval to the maximum of the two end times.
Step 3: If the current interval didn’t overlap with the last merged interval, I would simply add the current interval to the list of merged intervals.
Step 4: After processing the entire list of intervals, I would have the final list with all overlaps merged.
Step 5: I realized this could be done in O(n log n) time complexity because sorting the intervals takes O(n log n), and then merging the intervals in a single pass takes O(n). This seemed to be the most efficient approach.
02
Round
Medium
Video Call
Duration80 minutes
Interview date12 Nov 2024
Coding problem3
1. Sum Of Max And Min
Easy
10m average time
90% success
0/40
Asked in companies



You are given an array “ARR” of size N. Your task is to find out the sum of maximum and minimum elements in the array.
Follow Up:
Can you do the above task in a minimum number of comparisons?
Problem approach
Step 1: I began by iterating through the array and comparing each element with the current highest and lowest values. Initially, I set the first element as both the highest and lowest. This seemed like the simplest approach.
Step 2: The interviewer asked me to optimize the solution, as it could be done more efficiently without sorting or making multiple passes through the array.
Step 3: I then realized that I could achieve this in a single traversal by updating the highest and lowest values as I went through the array, comparing each element with the current maximum and minimum values. This reduced the complexity to O(n), which was much better.
2. Level Order Traversal
Easy
10m average time
90% success
0/40
Asked in companies



You are given a ‘Binary Tree’.
Return the level-order traversal of the Binary Tree.
Example:
Input: Consider the following Binary Tree:

Output:
Following is the level-order traversal of the given Binary Tree: [1, 2, 3, 5, 6, 4]
Problem approach
Step 1: Initially, I considered using recursion to traverse the tree, but I quickly realized that it wasn’t the best approach for visiting nodes level by level.
Step 2: So, I switched to using a queue. I added the root node to the queue and started processing its children one at a time.
Step 3: As I moved through each level, I kept adding the child nodes of the current level to the queue. This helped me traverse the tree level by level, and the interviewer seemed satisfied with how I approached the problem.
3. Cycle Detection In Undirected Graph
Moderate
0/80
Asked in companies



You have been given an undirected graph with 'N' vertices and 'M' edges. The vertices are labelled from 1 to 'N'.
Your task is to find if the graph contains a cycle or not.
A path that starts from a given vertex and ends at the same vertex traversing the edges only once is called a cycle.
Example :
In the below graph, there exists a cycle between vertex 1, 2 and 3.
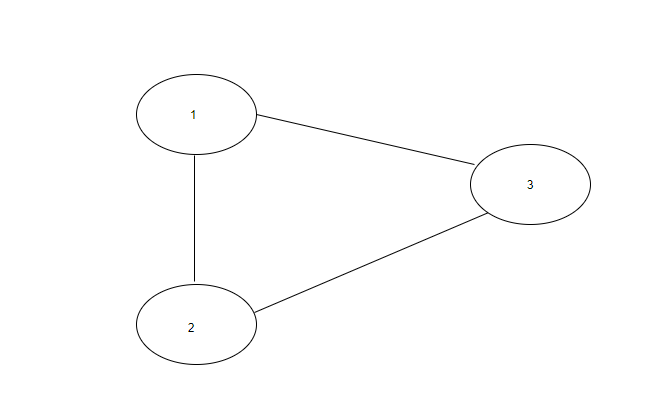
Note:
1. There are no parallel edges between two vertices.
2. There are no self-loops(an edge connecting the vertex to itself) in the graph.
3. The graph can be disconnected.
For Example :
Input: N = 3 , Edges = [[1, 2], [2, 3], [1, 3]].
Output: Yes
Explanation : There are a total of 3 vertices in the graph. There is an edge between vertex 1 and 2, vertex 2 and 3 and vertex 1 and 3. So, there exists a cycle in the graph.
Problem approach
Step 1: I started by iterating through the array and comparing each element with the current highest and lowest values. Initially, I set the first element as both the highest and lowest. This seemed like the simplest approach.
Step 2: The interviewer asked me to optimize the solution, as it could be done more efficiently without sorting or making multiple passes through the array.
Step 3: I then realized that I could achieve this in a single traversal by updating the highest and lowest values as I went through the array, comparing each element with the current maximum and minimum values. This way, I reduced the complexity to O(n), which was much more efficient.

Here's your problem of the day
Solving this problem will increase your chance to get selected in this company
Skill covered: Programming
What is the purpose of the return keyword?
Choose another skill to practice
Similar interview experiences
SDE - 1
3 rounds | 7 problems
Interviewed by OYO
4782 views
0 comments
0 upvotes
SDE - 1
3 rounds | 9 problems
Interviewed by Salesforce
3567 views
0 comments
0 upvotes
Fullstack developer Intern
2 rounds | 5 problems
Interviewed by FlexiEle Consulting Services (FE)
235 views
0 comments
0 upvotes
Fullstack Developer
2 rounds | 1 problems
Interviewed by FlexiEle Consulting Services (FE)
139 views
0 comments
0 upvotes




